初中数学苏科版七年级下册7.4 认识三角形导学案及答案

这是一份初中数学苏科版七年级下册7.4 认识三角形导学案及答案，文件包含74认识三角形2-学生docx、74认识三角形2-教师docx等2份学案配套教学资源，其中学案共16页， 欢迎下载使用。
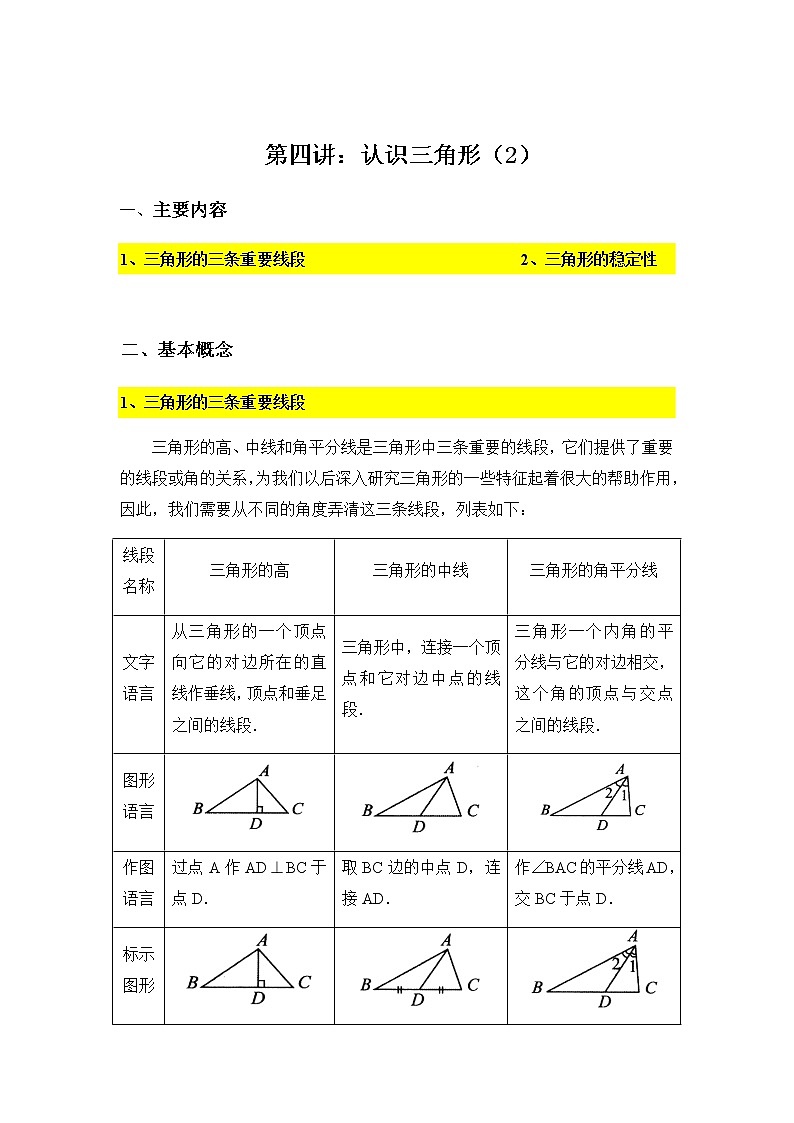
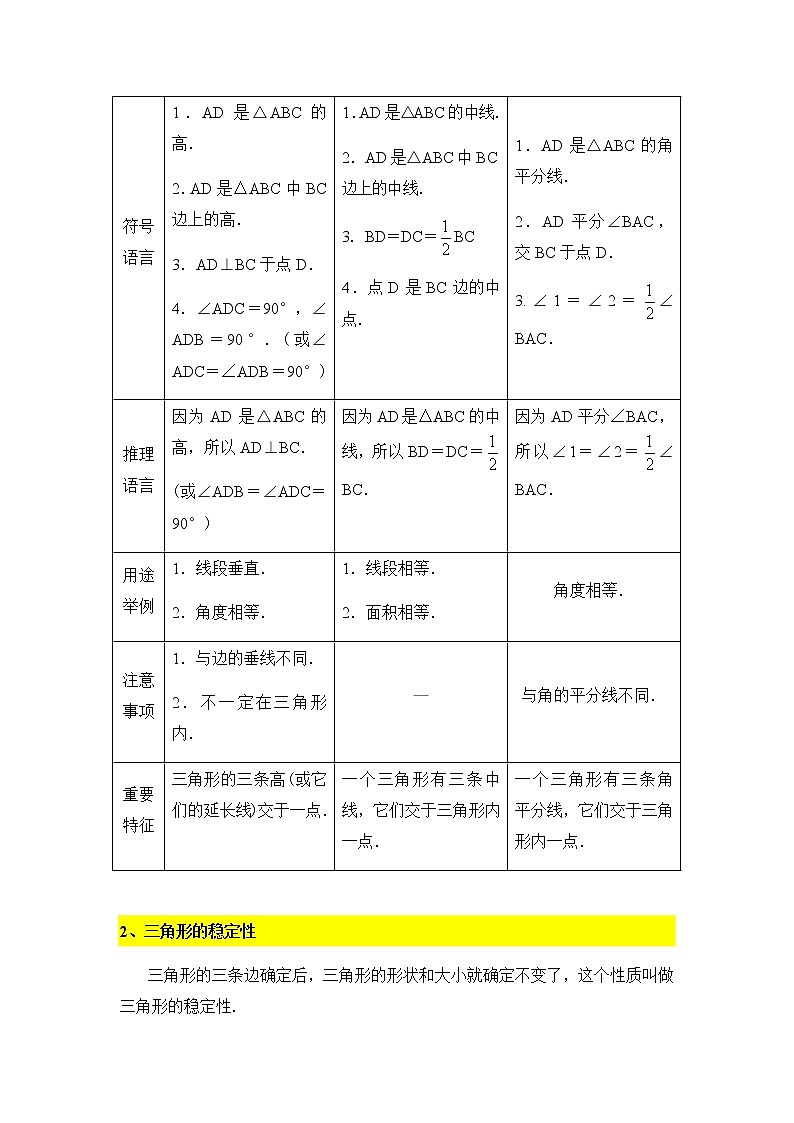
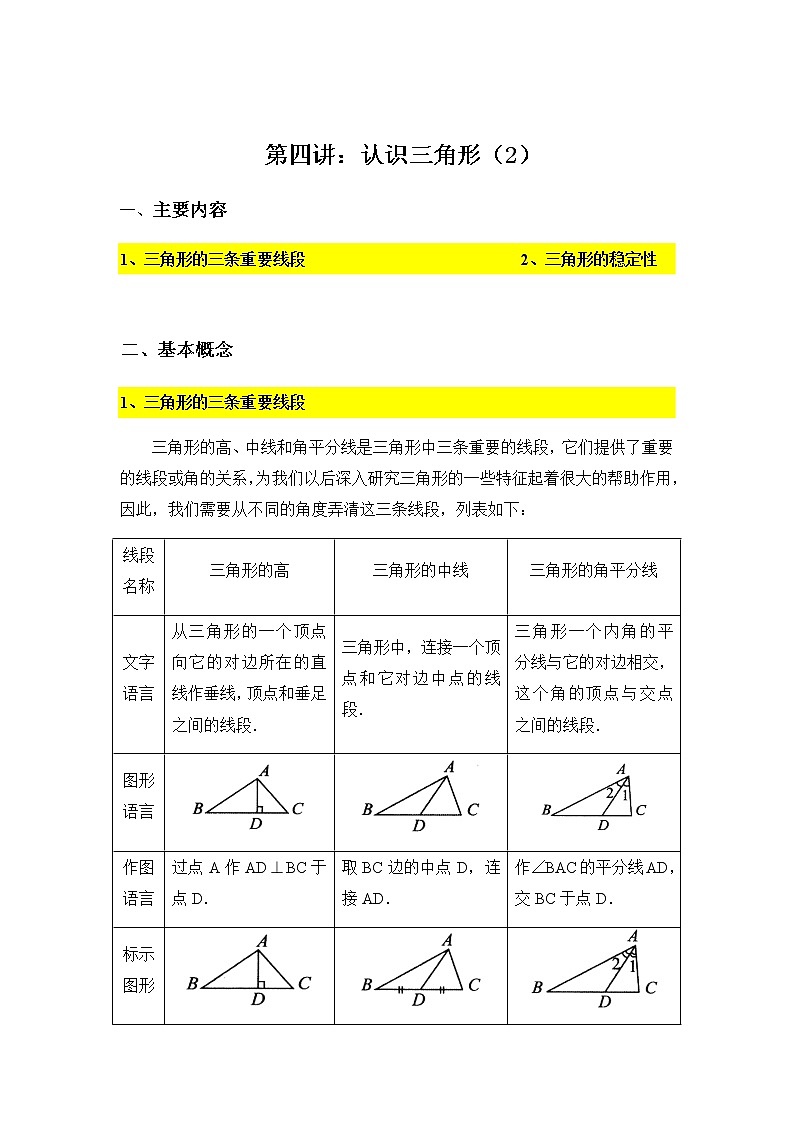
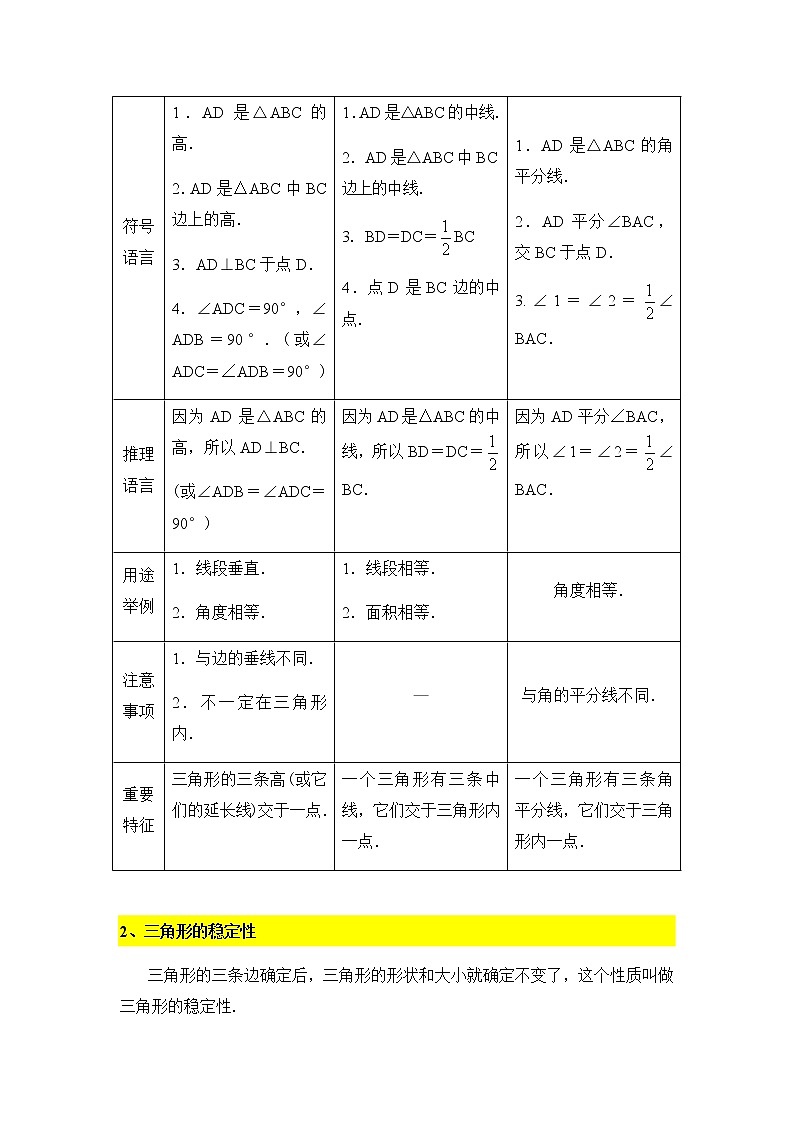
 第四讲：认识三角形（2）一、主要内容      1、三角形的三条重要线段                           2、三角形的稳定性    二、基本概念1、三角形的三条重要线段三角形的高、中线和角平分线是三角形中三条重要的线段，它们提供了重要的线段或角的关系，为我们以后深入研究三角形的一些特征起着很大的帮助作用，因此，我们需要从不同的角度弄清这三条线段，列表如下：线段名称三角形的高三角形的中线三角形的角平分线文字语言从三角形的一个顶点向它的对边所在的直线作垂线，顶点和垂足之间的线段．三角形中，连接一个顶点和它对边中点的线段．三角形一个内角的平分线与它的对边相交，这个角的顶点与交点之间的线段．图形语言作图语言过点A作AD⊥BC于点D．取BC边的中点D，连接AD．作∠BAC的平分线AD，交BC于点D．标示图形符号语言1．AD是△ABC的高．2．AD是△ABC中BC边上的高．3．AD⊥BC于点D．4．∠ADC＝90°，∠ADB＝90°．(或∠ADC＝∠ADB＝90°)1．AD是△ABC的中线．2．AD是△ABC中BC边上的中线．3．BD＝DC＝BC4．点D是BC边的中点．1．AD是△ABC的角平分线．2．AD平分∠BAC，交BC于点D．3.∠1＝∠2＝∠BAC．推理语言因为AD是△ABC的高，所以AD⊥BC．(或∠ADB＝∠ADC＝90°)因为AD是△ABC的中线，所以BD＝DC＝BC．因为AD平分∠BAC，所以∠1＝∠2＝∠BAC．用途举例1．线段垂直．2．角度相等．1．线段相等．2．面积相等．角度相等．注意事项1．与边的垂线不同．2．不一定在三角形内．—与角的平分线不同．重要特征三角形的三条高(或它们的延长线)交于一点．一个三角形有三条中线，它们交于三角形内一点．一个三角形有三条角平分线，它们交于三角形内一点． 2、三角形的稳定性     三角形的三条边确定后，三角形的形状和大小就确定不变了，这个性质叫做三角形的稳定性.   要点诠释：（1）三角形的形状固定是指三角形的三个内角不会改变，大小固定指三条边长不改变． （2）三角形的稳定性在生产和生活中很有用．例如，房屋的人字梁具有三角形的结构，它就坚固而稳定；在栅栏门上斜着钉一条(或两条)木板，构成一个三角形，就可以使栅栏门不变形．大桥钢架、输电线支架都采用三角形结构，也是这个道理．  （3）四边形没有稳定性，也就是说，四边形的四条边长确定后，不能确定它的形状，它的各个角的大小可以改变．四边形的不稳定性也有广泛应用，如活动挂架，伸缩尺．有时我们又要克服四边形的不稳定性，如在门框未安好之前，先在门框上斜着钉一根木板，使它不变形． 1.如图，过△ABC的顶点A，作BC边上的高，以下作法正确的是（　　）A． B． C． D．【答案】A2.如图所示，CD为△ABC的AB边上的中线，△BCD的周长比△ACD的周长大3cm，BC＝8cm，求边AC的长．★★ 【答案与解析】5cm∵CD为△ABC的AB边上的中线，∴AD=BD∵△BCD的周长=BC+CD=BD，△ACD的周长=AC+CD+AD∴△BCD的周长-△ACD的周长=BC-AC=3cm∵BC＝8cm,∴AC=5cm 3. 如图所示，木工师傅在做完门框后，为防止变形常常像图中那样钉上两条斜拉的木板条(即AB、CD)，这样做的数学道理是什么?【答案与解析】 解：三角形的稳定性．【总结升华】本题是三角形的稳定性在生活中的具体应用．实际生活中，将多边形转化为三角形都是为了利用三角形的稳定性． 三、课堂讲解                             1、如图，AD为△ABC的中线，BE为△ABD的中线．（1）猜想：△ABD与△ADC的面积有何关系？并简要说明理由；（2）在△BED中作BD边上的高；（3）若△ABC的面积为40，BD=5，则△BDE中BD边上的高为多少？  【答案】解：（1）△ABD与△ADC的面积相等，理由如下：作AF⊥BC，如图1：因为BD=DC，AF=AF，所以△ABD与△ADC的面积相等；  （2）作图，如图2：（3）因为△ABC的面积为40，BD=5，所以△ABD的面积为20，因为BE为△ABD的中线，所以△BDE的面积为10，所以△BDE中BD边上的高为4．2、如图，我们知道要使四边形木架不变形，至少要钉一根木条．那么要使五边形木架不变形，至少要钉几根木条?使七边形木架不变形，至少要钉几根木条?使n边形木架不变形．又至少要钉多少根木条?【答案】要使五边形木架不变形，至少要钉2根木条；使七边形木架不变形，至少要钉4根木条；使n边形木架不变形，至少要钉(n-3)根木条． 【达标检测】一、选择题1．三角形的角平分线、中线和高都是 (    ) ．    A．直线    B．线段    C．射线    D．以上答案都不对 2．下列说法不正确的是 (    )   A．三角形的中线在三角形的内部    B．三角形的角平分线在三角形的内部   C．三角形的高在三角形的内部      D．三角形必有一高线在三角形的内部 3．如图，AM是△ABC的中线，那么若用S1表示△ABM的面积，用S2表示△ACM的面积，则S1和S2的大小关系是(   ) ．A．S1＞S2    B．S1＜S2    C．S1＝S2    D．以上三种情况都有可能 4．如图，一扇窗户打开后，用窗钩AB可将其固定，这里所运用的几何原理是(   ) ．    A．三角形的稳定性        B．两点之间线段最短    C．两点确定一条直线      D．垂线段最短 二、填空题5.不一定在三角形内部的线段是　　（填“角的平分线”或“高线”或“中线”）．6.如图，AD是△ABC的角平分线，则∠______＝∠______＝∠_______；BE是△ABC的中线，则________＝_______＝________；CF是△ABC的高，则∠________＝∠________＝90°，CF________AB．7.如图，AD、AE分别是△ABC的高和中线，已知AD＝5cm，CE＝6cm，则△ABE和△ABC的面积分别为________________． 8.如果知道三角形的一边之长和这边上的高，三角形________确定．(填“能”或“不能”) 三、解答题9.已知AD是△ABC的高，∠BAD＝70°，∠CAD＝20°，（1）求∠BAC的度数．（2）△ABC是什么三角形．  【答案与解析】一、选择题1.B     2.C     3.C      4.A二、填空题5. 高线．6. BAD  CAD  BAC； AE   CE   AC；   AFC  BFC  ⊥7.15cm2，30cm2；8.能；三、解答题9.解：（1）当高AD在△ABC的内部时(如图(1))．因为∠BAD＝70°，∠CAD＝20°，所以∠BAC＝∠BAD+∠CAD＝70°+20°＝90°．    当高AD在△ABC的外部时(如图(2))．    因为∠BAD＝70°，∠CAD＝20°，    所以∠BAC＝∠BAD-∠CAD＝70°-20°＝50°．综上可知∠BAC的度数为90°或50°．（2）如图(1)，当AD在△ABC的内部时，    因为∠BAC＝∠BAD+∠CAD＝70°+20°＝90°，    所以△ABC是直角三角形．如图(2)，当AD在△ABC的外部时，因为∠BAC＝∠BAD-∠CAD＝70°-20°＝50°，∠ABC＝90°-∠BAD＝90°-70°＝20°，所以∠ACB＝180°-∠ABC-∠BAC＝180°-50°-20°＝110°．    所以△ABC为钝角三角形．    综上可知，△ABC是直角三角形或钝角三角形．