高中物理鲁科版 (2019)选择性必修 第一册第1节 波的形成和描述第2课时教案设计

这是一份高中物理鲁科版 (2019)选择性必修 第一册第1节 波的形成和描述第2课时教案设计，共1页。教案主要包含了波的图像的应用，波的图像与振动图像对比x/m，机械波的多解问题等内容，欢迎下载使用。

教学目标
理解波的图像的意义．
能够由波的图像判断传播方向与质点振动方向的关系
会区别波动图像和振动图像．
波的图像的周期性和波的传播方向的双向性应用。
教学重难点
教学重点
波的图像与振动图像的对比。
波的图像的周期性和波的传播方向的双向性的理解
教学难点
由波传播方向判断质点振动方向或由质点的振动方向判断波的传播方向。
波的图像的周期性和波的传播方向的双向性应用。
教学准备
多媒体课件
教学过程
新课引入
复习回顾：关于波的图像
1.图像的横、纵坐标分别表示什么物理量？
横轴表示时间各质点的平衡位置,纵轴表示某一时刻各质点偏离平衡位置的位移.
2.从简谐运动图像可以求哪些物理量 ?
（1）振幅A:图像的峰值.
（2）波长λ:相邻两个波峰或波谷之间的距离.
（3）各个质点的位移x:对应于图像上某一点的坐标（x，y）．
思考：如何根据波的传播方向判断质点的振动方向？
讲授新课
一、波的图像的应用
1.波的传播方向和质点的振动方向之间的关系。
⑴带动法（又称追随法，即靠近波源的质点带动后面的质点振动，或远离波源的质点追随前面的质点振动。）
Q′
Q
P′
x/m
y/cm
5
-5
0
2
4
6
v
P
步骤1：明确波的传播方向，确定波源位置；
步骤2：在某质点P（Q）靠近波源一方（紧挨着P点）图像上找另外一点P′（Q′）；
步骤3：若P′在P下方，则P′带动P向下运动；若Q′在Q上方，则Q'带动Q向上运动。
思考：如果已知P点的振动方向向下，判断波的传播方向．
解析：P点的振动方向向下，说明它要追随左面的点，故波源在左，波向右传播。
v
微平移法：做出经微小时间后的波形,就知道了各质点经过Δt时间达到的位置,运动方向就可确定.
Y
X
O
v
下坡上
上坡下
上坡下
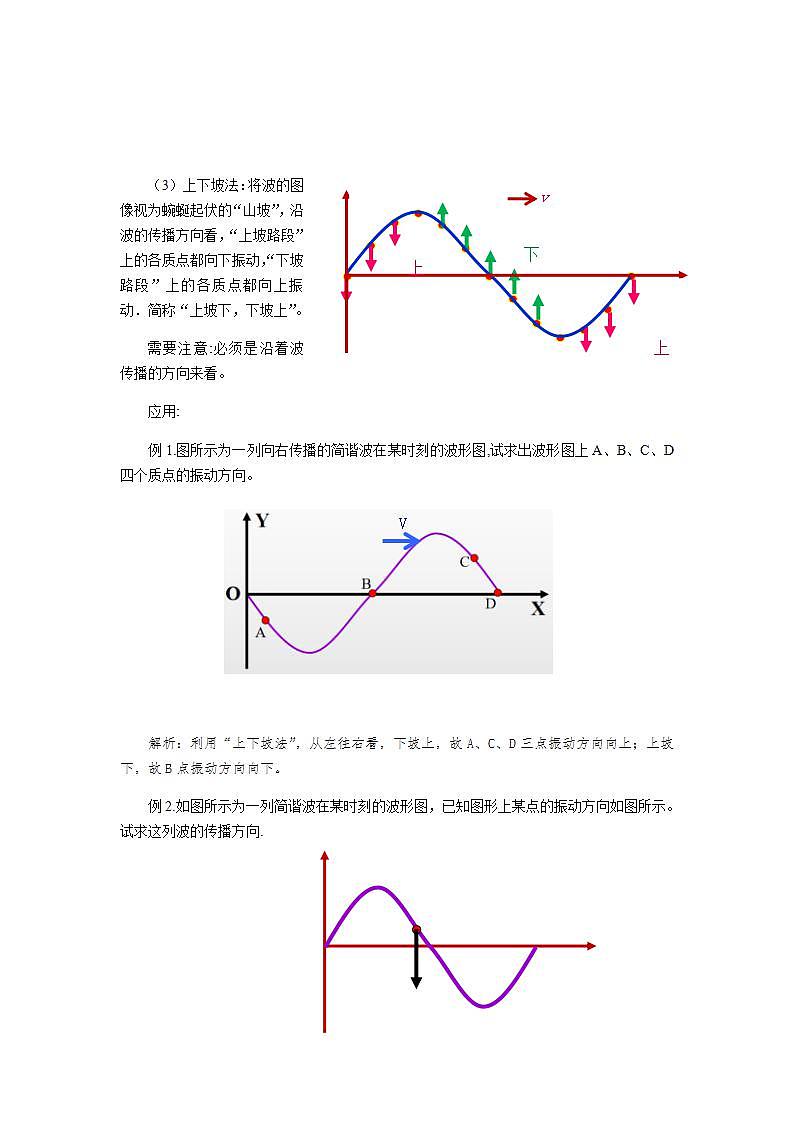
上下坡法：将波的图像视为蜿蜒起伏的“山坡”，沿波的传播方向看，“上坡路段”上的各质点都向下振动，“下坡路段”上的各质点都向上振动．简称“上坡下，下坡上”。
需要注意:必须是沿着波传播的方向来看。
应用:
例1.图所示为一列向右传播的简谐波在某时刻的波形图,试求出波形图上A、B、C、D四个质点的振动方向。
V
解析：利用“上下坡法”，从左往右看，下坡上，故A、C、D三点振动方向向上；上坡下，故B点振动方向向下。
Y
X
O
v
例2.如图所示为一列简谐波在某时刻的波形图，已知图形上某点的振动方向如图所示。试求这列波的传播方向.
解析：利用带动法，质点振动方向向下，说明右侧的点距离波源近，波的传播方向向左。
2.求波在某时刻的波形图
（1）特殊点法：先找出两点（平衡位置和波峰及波谷特殊点）并确定其运动方向；然后确定经△t时间内这两点所达到的位置；最后按正弦规律画出新的波形。
x/m
y/m
0
1
2
3
4
v
画出再经t=T/4时的波形图
P
P′
Q′
Q
（2）图象平移法：经过时间△t，波在传播方向移动的距离x=v△t,因此，把图象沿传播方向平移x即得到相对应的图象.
x/m
y/m
0
1
2
3
4
v
当△t=时，x=。
二、波的图像与振动图像对比x/m
y/m
0
1
2
3
4
t/s
y/m
0
1
2
3
4
判断：哪个是振动图像？哪个是波形图？图线随时间如何变化？
解析：关键看横轴，是时间轴的表示振动图像，由图可知第一个表示波形图，λ=4m，第二个表示振动图像，T=4s。下一时刻的波形图，需要把波形沿运动方向平移得到，而振动图像直接延伸即可。
三、机械波的多解问题
因机械波的图像具有周期性，经过T或nT的时间，图像会重复，这就造成了波动问题的多解性。多解的主要因素有：
1．周期性
(1)时间的周期性：时间间隔Δt与周期T的关系不明确．
(2)空间的周期性：波传播距离Δx与波长λ的关系不明确．
2．双向性
(1)传播方向双向性：波的传播方向不确定．
(2)振动方向双向性：质点振动方向不明确．
由于波动问题的多解性的出现，从而导致了求解波动问题的复杂性，而最容易失误的往往是漏解，因此在解决振动和波动问题时一定要考虑全面，尤其是对题设条件模糊，没有明确说明的物理量，一定要考虑其所有可能性．如说质点达到最大位移处，则有正向最大位移与负向最大位移两种可能；质点由平衡位置起振，起振方向有向上向下两种可能；只告诉波速不说传播方向，应考虑沿两个方向传播的可能；若给出两时刻的波形，则有可能是波形重复多次后又变至题目所给的相应的后一种波形．解决此类问题时，往往采用从特殊到一般的思维方法，即找到一个周期内满足条件的特例，在此基础上，时间关系加nT(n＝0,1,2…)；空间关系加nλ(n＝0,1,2…)．总之，只要有多解意识，再根据题意仔细分析，就能得到全部的解．
应用：
例3：如图所示，实线是某时刻的波形图象，虚线是0.2 s后的波形图．
(1)若波向左传播，求它的可能周期和最大周期；
(2)若波向右传播，求它的可能传播速度；
(3)若波速是45 m/s，求波的传播方向．
解析：在已知两个时刻的波形图来求波的周期或波速时，一定要考虑到两个方面：一个是波传播的双向性；一个是它的周期性带来的多解性．
(1)波向左传播，传播的时间为Δt＝eq \f(3,4)T＋nT(n＝0,1，2，…)，
所以T＝eq \f(4Δt,4n＋3)＝4×eq \f(0.2,4n＋3) s＝ s(n＝0,1,2,3，…)，
当n=0时，最大周期为Tmax＝ s≈0.27 s.
(2)波向右传播Δt＝eq \f(T,4)＋nT(n＝0,1,2,3…)
所以T＝eq \f(0.8,4n＋1) s(n＝0,1,2…)，而λ＝4 m
所以v＝eq \f(λ,T)＝5(4n＋1) m/s(n＝0,1,2…)．
(3)波速是45 m/s，设波向右传播，由上问求得的向右传播的波速公式得45 m/s＝5(4n＋1) m/s，解得n＝2.故假设成立，波向右传播．
总结：由于没有明确波的传播方向，则两波形所间隔的时间与周期的关系是不明确的，解此类问题，可以假设向右传播，对问题进行处理，得出一系列结论，然后再假设向左传播得出一系列结论．在解决波动问题时，一定要注意考虑波传播方向的双向性，以及时间的周期性和空间的周期性，即Δt＝nT＋t，Δx＝nλ＋x(n＝0,1,2…)．
典题剖析
例1 一列简谐波在t=0时刻的波形如图甲所示,图乙表示该波传播的介质中某质点此后一段时间内的振动图像,则( )
A.若波沿x轴正方向传播,图乙应为a点的振动图像
B.若波沿x轴正方向传播,图乙应为b点的振动图像
C.若波沿x轴正方向传播,图乙应为c点的振动图像
D.若波沿x轴正方向传播,图乙应为d点的振动图像
答案：B
解析：在图乙的振动图像中，t=0时刻质点在平衡位置并向y轴的正方向运动，而图甲的波形却表明在t=0时刻质点b、d在平衡位置，而a、c不在平衡位置，故选项A、C判断错误；若波沿x轴正方向传播，质点b向上运动，d向下运动，故选项B判断正确，选项D判断错误。
例2 周期为2.0 s的简谐横波沿x轴传播，该波在某时刻的图象如图所示，此时质点P沿y轴负方向运动，则该波( )
A．沿x轴正方向传播，波速v＝20 m/s
B．沿x轴正方向传播，波速v＝10 m/s
C．沿x轴负方向传播，波速v＝20 m/s
D．沿x轴负方向传播，波速v＝10 m/s
答案：B
解析：由质点P沿y轴负方向运动，可知波沿x轴正方向传播，波速v＝eq \f(λ,T)＝eq \f(20 m,2.0 s)＝10 m/s，B项正确．
例3(多选)如图，一列简谐横波沿x轴正方向传播，实线为t＝0时的波形图，虚线为t＝0.5 s时的波形图．已知该简谐波的周期大于0.5 s．关于该简谐波，下列说法正确的是( )
A．波长为2 m
B．波速为6 m/s
C．频率为1.5 Hz
D．t＝2 s时，x＝2 m处的质点经过平衡位置
答案：BCD
解析：由图象可知简谐横波的波长为λ＝4 m，A项错误；波沿x轴正向传播，t＝0.5 s＝（n+）T，可得周期T＝ s、由于T>0.5s，所以n=0，T=s，频率f＝＝1.5 Hz，波速v＝λf＝6 m/s，B、C项正确；t＝0时刻，x＝2 m处的质点在平衡位置，经过2 s＝3T，质点一定经过平衡位置，D项正确．
波的描述
由波的传播方向判断质点的振动方向
带动法
微平移法
上下坡法
求下一时刻的波形图
图像平移法
特殊点法
波的图像与振动图像对比
机械波的多解问题
双向性
周期性
由质点的振动方向判断波的传播方向
课堂小结
振动图像和波动图像的比较
特点
振动图像
波动图像
相同点
图像形状
正（余）弦曲线
纵坐标最大值
振幅
不同点
纵坐标
不同时刻
某一质点的位移
某一时刻
所有质点的位移
横坐标
时间
各点平衡位置与原点的
距离x
描述对象
某个振动质点
一群质点
物理意义
某一质点
不同时刻
离开平衡位置的位移
某一时刻
各个质点
离开平衡位置的位移
最大值间距的含义
周期
波长
图形随时间变化
图像延伸
已有的图像形状不变
沿传播方向平移