2019-2020学年河南省平顶山市汝州市九年级（上）期末数学试卷

这是一份2019-2020学年河南省平顶山市汝州市九年级（上）期末数学试卷，共26页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
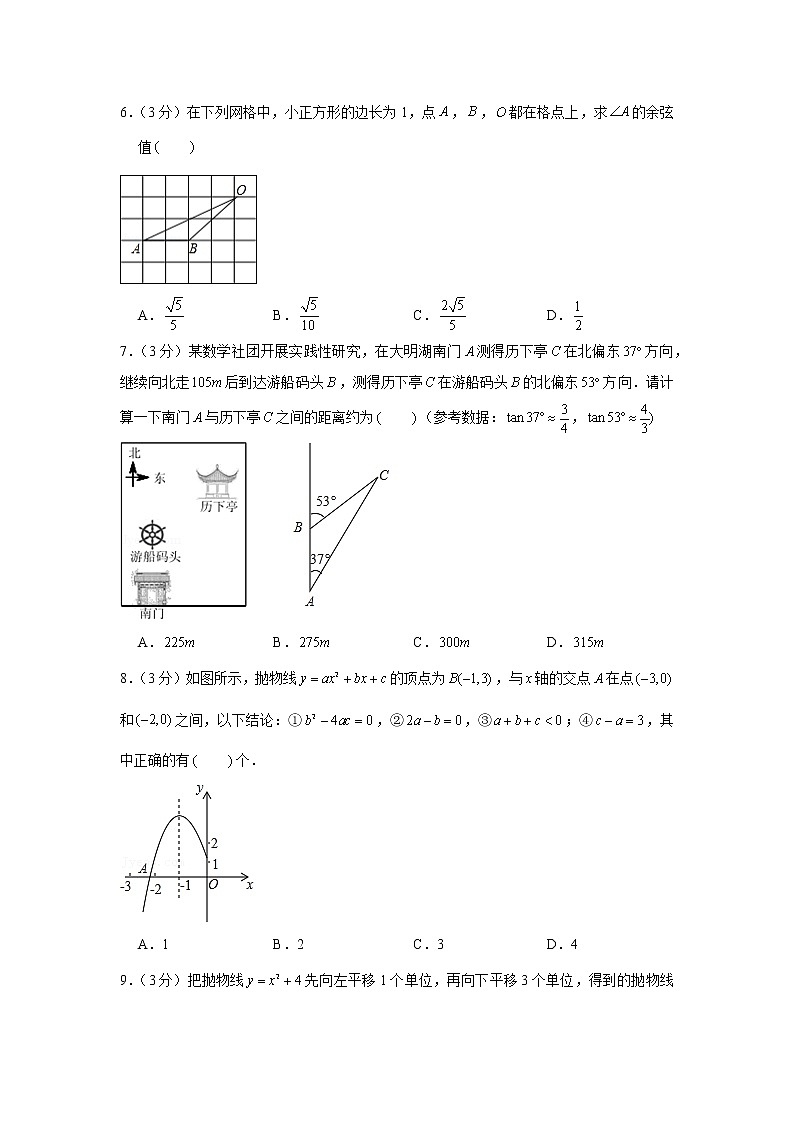
2019-2020学年河南省平顶山市汝州市九年级（上）期末数学试卷一、选择题（本题共计10小题，每题3分，共计30分）1．（3分）一个菱形的边长是方程的一个根，其中一条对角线长为8，则该菱形的面积为　　A．48 B．24 C．24或40 D．48或802．（3分）在一个密闭不透明的袋子里有若干个白球．为估计白球个数，小何向其中投入8个黑球，搅拌均匀后随机摸出一个球，记下颜色，再把它放入袋中，不断重复摸球400次，其中88次摸到黑球，则估计袋中大约有白球　　A．18个 B．28个 C．36个 D．42个3．（3分）如图，已知，它们依次交直线、于点、、和点、、，如果，，那么等于　　A． B． C． D．4．（3分）如图，是由几个大小相同的小立方块所搭几何体的俯视图，其中小正方形中的数字表示在该位置的小立方块的个数，你认为从左面看到的这个几何体的形状图是　　A． B． C． D．5．（3分）已知函数，当时，的取值范围是　　A． B． C．或 D．或6．（3分）在下列网格中，小正方形的边长为1，点，，都在格点上，求的余弦值　　A． B． C． D．7．（3分）某数学社团开展实践性研究，在大明湖南门测得历下亭在北偏东方向，继续向北走后到达游船码头，测得历下亭在游船码头的北偏东方向．请计算一下南门与历下亭之间的距离约为　　（参考数据：，A． B． C． D．8．（3分）如图所示，抛物线的顶点为，与轴的交点在点和之间，以下结论：①，②，③；④，其中正确的有　　个．A．1 B．2 C．3 D．49．（3分）把抛物线先向左平移1个单位，再向下平移3个单位，得到的抛物线的解析式为　　A． B． C． D．10．（3分）某公司今年4月的营业额为2500万元，按计划第二季度的总营业额要达到9100万元，设该公司5、6两月的营业额的月平均增长率为．根据题意列方程，则下列方程正确的是　　A． B． C． D．二、填空题（本题共计5小题，每题3分，共计15分，）11．（3分）有一个抛物线形拱桥，其最大高度为16米，跨度为40米，现把它的示意图放在如图所示的平面直角坐标系中，则此抛物线的解析式为　　．12．（3分）如图，在一块长，宽的矩形空地上，修建同样宽的两条互相垂直的道路（两条道路各与矩形的一条边平行），剩余部分栽种花草，且栽种花草的面积为，设道路的宽为，则根据题意，可列方程为 　　．13．（3分）如图，点、在反比例函数的图象上，过点、作轴的垂线，垂足分别为、，延长线段交轴于点，若，的面积为6，则的值为　 　．14．（3分）如图，矩形的两边落在坐标轴上，反比例函数的图象在第一象限的分支过的中点交于点，连接，若的面积为12，则　　．15．（3分）如图矩形中，，，点为上一个动点，把沿折叠，当点的对应点落在的角平分线上时，的长为　　．三、解答题（本题共计8小题，共计75分，）16．（8分）在平面直角坐标系中，已知抛物线的顶点为，图象与轴交于、两点（点在点的左侧）．（1）求的取值范围；（2）当取最大整数时，求的面积．17．（9分）春节期间的一天晚上，小玲和小林去看灯展，当小林站在灯杆和灯杆之间的点处，小林的身高为，小玲发现了奇怪的一幕：小林在灯的照射下，影子恰好落在灯杆的底部点处，小林在灯的照射下，影子恰好落在灯杆的底部点处．如图，已知、、都与垂直，垂足分别是、、，且，，求小林的身高．18．（9分）如图，地在地的正东方向，因有大山阻隔，由地到地需要绕行地，已知地位于地北偏东方向，距离地，地位于地南偏东方向，若打通穿山隧道，建成两地直达高铁，求地到地之间高铁线路的长（结果保留整数）（参考数据：；；19．（9分）如图，已知，是一次函数的图象和反比例函数的图象的两个交点．（1）求反比例函数和一次函数的解析式；（2）求直线与轴的交点的坐标及的面积；（3）直接写出一次函数的值小于反比例函数值的的取值范围．20．（9分）已知矩形的一条边，将矩形折叠，使得顶点落在边上的点处．如图，已知折痕与边交于点，连接、、．（1）求证：；（2）若，求边的长．21．（10分）某公司研发了一款成本为50元的新型玩具，投放市场进行试销售．其销售单价不低于成本，按照物价部门规定，销售利润率不高于，市场调研发现，在一段时间内，每天销售数量（个与销售单价（元符合一次函数关系，如图所示：（1）根据图象，直接写出与的函数关系式．（2）该公司要想每天获得3000元的销售利润，销售单价应定为多少元？（3）销售单价为多少元时，每天获得的利润最大，最大利润是多少元？22．（10分）如图1，在中，，，点，分别在边，上，，连接，点，，分别为，，的中点．（1）观察猜想图1中，线段与的数量关系是　　，的度数是　　；（2）探究证明把绕点逆时针方向旋转到图2的位置，连接，，，判断的形状，并说明理由；（3）拓展延伸把绕点在平面内自由旋转，若，，请直接写出面积的取值范围．23．（11分）如图，抛物线的对称轴为直线，抛物线交轴于、两点，与直线交于、两点，直线与抛物线的对称轴交于点．（1）求抛物线的解析式．（2）点在直线上方的抛物线上运动，若的面积最大，求此时点的坐标．（3）在平面直角坐标系中，以点、、、为顶点的四边形是平行四边形，请直接写出符合条件点的坐标．
2019-2020学年河南省平顶山市汝州市九年级（上）期末数学试卷参考答案与试题解析一、选择题（本题共计10小题，每题3分，共计30分）1．（3分）一个菱形的边长是方程的一个根，其中一条对角线长为8，则该菱形的面积为　　A．48 B．24 C．24或40 D．48或80【解答】解：，所以，，菱形一条对角线长为8，菱形的边长为5，菱形的另一条对角线为，菱形的面积．故选：．2．（3分）在一个密闭不透明的袋子里有若干个白球．为估计白球个数，小何向其中投入8个黑球，搅拌均匀后随机摸出一个球，记下颜色，再把它放入袋中，不断重复摸球400次，其中88次摸到黑球，则估计袋中大约有白球　　A．18个 B．28个 C．36个 D．42个【解答】解：由题意可得，白球的个数大约为：，故选：．3．（3分）如图，已知，它们依次交直线、于点、、和点、、，如果，，那么等于　　A． B． C． D．【解答】解：，，，，，．故选：．4．（3分）如图，是由几个大小相同的小立方块所搭几何体的俯视图，其中小正方形中的数字表示在该位置的小立方块的个数，你认为从左面看到的这个几何体的形状图是　　A． B． C． D．【解答】解：由俯视图知该几何体共2列，其中第1列前一排1个正方形、后1排2个正方形，第2列只有前排2个正方形，所以从左面看到的这个几何体的形状图是：故选：．5．（3分）已知函数，当时，的取值范围是　　A． B． C．或 D．或【解答】解：函数中，在每个象限内随着的增大而增大，当时，，当时，，当时，，即或，故选：．6．（3分）在下列网格中，小正方形的边长为1，点，，都在格点上，求的余弦值　　A． B． C． D．【解答】解：，，故选：．7．（3分）某数学社团开展实践性研究，在大明湖南门测得历下亭在北偏东方向，继续向北走后到达游船码头，测得历下亭在游船码头的北偏东方向．请计算一下南门与历下亭之间的距离约为　　（参考数据：，A． B． C． D．【解答】解：如图，作于．设，．在中，，即，在中，，即，解得，，，故选：．8．（3分）如图所示，抛物线的顶点为，与轴的交点在点和之间，以下结论：①，②，③；④，其中正确的有　　个．A．1 B．2 C．3 D．4【解答】解：抛物线与轴有两个交点，△，，故①错误；由于对称轴为，与关于对称，时，，时，，故③正确；对称轴为，，故②正确；顶点为，，，即，故④正确；故选：．9．（3分）把抛物线先向左平移1个单位，再向下平移3个单位，得到的抛物线的解析式为　　A． B． C． D．【解答】解：将抛物线向左平移1个单位所得直线解析式为：；再向下平移3个单位为：，即．故选：．10．（3分）某公司今年4月的营业额为2500万元，按计划第二季度的总营业额要达到9100万元，设该公司5、6两月的营业额的月平均增长率为．根据题意列方程，则下列方程正确的是　　A． B． C． D．【解答】解：设该公司5、6两月的营业额的月平均增长率为．根据题意列方程得：．故选：．二、填空题（本题共计5小题，每题3分，共计15分，）11．（3分）有一个抛物线形拱桥，其最大高度为16米，跨度为40米，现把它的示意图放在如图所示的平面直角坐标系中，则此抛物线的解析式为　　．【解答】解：因为抛物线过点和，①又函数过点代入①得，解得．抛物线的解析式为；故答案为．12．（3分）如图，在一块长，宽的矩形空地上，修建同样宽的两条互相垂直的道路（两条道路各与矩形的一条边平行），剩余部分栽种花草，且栽种花草的面积为，设道路的宽为，则根据题意，可列方程为 　　．【解答】解：道路的宽应为米，由题意得，，故答案为：．13．（3分）如图，点、在反比例函数的图象上，过点、作轴的垂线，垂足分别为、，延长线段交轴于点，若，的面积为6，则的值为　4　．【解答】解：设，点在反比例函数，，，，，解得．故答案为：4．14．（3分）如图，矩形的两边落在坐标轴上，反比例函数的图象在第一象限的分支过的中点交于点，连接，若的面积为12，则　　．【解答】解：如图，过点、分别作轴的垂线，垂足分别为、，则，又，，，，，，．故答案为．15．（3分）如图矩形中，，，点为上一个动点，把沿折叠，当点的对应点落在的角平分线上时，的长为　或　．【解答】解：如图，连接，过作，交于点，于点，作交于点点的对应点落在的角平分线上，，设，则，，又折叠图形可得，，解得或4，即或4．在中，设，①当时，，，，，解得，即，②当时，，，，，解得，即．故答案为：或．三、解答题（本题共计8小题，共计75分，）16．（8分）在平面直角坐标系中，已知抛物线的顶点为，图象与轴交于、两点（点在点的左侧）．（1）求的取值范围；（2）当取最大整数时，求的面积．【解答】解：（1）抛物线与轴有两个交点，令．．与轴有两个交点，方程有两个不等的实数根．△．即△，． （2），且取最大整数，．当时，抛物线．坐标为．令，得，解得，．抛物线与轴两个交点的坐标为，，的面积为．17．（9分）春节期间的一天晚上，小玲和小林去看灯展，当小林站在灯杆和灯杆之间的点处，小林的身高为，小玲发现了奇怪的一幕：小林在灯的照射下，影子恰好落在灯杆的底部点处，小林在灯的照射下，影子恰好落在灯杆的底部点处．如图，已知、、都与垂直，垂足分别是、、，且，，求小林的身高．【解答】解：，，都与垂直，，，，，由①②得：，，，，，答：小林的身高为．18．（9分）如图，地在地的正东方向，因有大山阻隔，由地到地需要绕行地，已知地位于地北偏东方向，距离地，地位于地南偏东方向，若打通穿山隧道，建成两地直达高铁，求地到地之间高铁线路的长（结果保留整数）（参考数据：；；【解答】解：过点作于点，地位于地北偏东方向，距离地，，，．地位于地南偏东方向，，，．答：地到地之间高铁线路的长为．19．（9分）如图，已知，是一次函数的图象和反比例函数的图象的两个交点．（1）求反比例函数和一次函数的解析式；（2）求直线与轴的交点的坐标及的面积；（3）直接写出一次函数的值小于反比例函数值的的取值范围．【解答】解：在反比例函数的图象上，，反比例函数解析式为：，把代入，得，解得，则点坐标为．把，分别代入，得，解得，一次函数的解析式为； （2），当时，，点的坐标为：，的面积的面积的面积； （3）由图象可知，当或时，一次函数的值小于反比例函数的值．20．（9分）已知矩形的一条边，将矩形折叠，使得顶点落在边上的点处．如图，已知折痕与边交于点，连接、、．（1）求证：；（2）若，求边的长．【解答】（1）证明：四边形为矩形，．由折叠，可知：，．，，；（2）解：由折叠，可知：，，，．，．，．设，则，，，解得：，．21．（10分）某公司研发了一款成本为50元的新型玩具，投放市场进行试销售．其销售单价不低于成本，按照物价部门规定，销售利润率不高于，市场调研发现，在一段时间内，每天销售数量（个与销售单价（元符合一次函数关系，如图所示：（1）根据图象，直接写出与的函数关系式．（2）该公司要想每天获得3000元的销售利润，销售单价应定为多少元？（3）销售单价为多少元时，每天获得的利润最大，最大利润是多少元？【解答】解：（1）设，为常数）将点，代入得解得与的函数关系式为：（2）由题意得：化简得：解得：，（不符合题意，舍去）答：销售单价为80元．（3）设每天获得的利润为元，由题意得，抛物线开口向下有最大值，当时，答：销售单价为90元时，每天获得的利润最大，最大利润是3200元．22．（10分）如图1，在中，，，点，分别在边，上，，连接，点，，分别为，，的中点．（1）观察猜想图1中，线段与的数量关系是　　，的度数是　　；（2）探究证明把绕点逆时针方向旋转到图2的位置，连接，，，判断的形状，并说明理由；（3）拓展延伸把绕点在平面内自由旋转，若，，请直接写出面积的取值范围．【解答】解：（1）点，是，的中点，，，点，是，的中点，，，，，，，，，，，，，，故答案为：，； （2）是等边三角形．由旋转知，，，，，，，利用三角形的中位线得，，，，是等腰三角形，同（1）的方法得，，，同（1）的方法得，，，，，，，，是等边三角形； （3）由（2）知，是等边三角形，，最大时，面积最大，最小时，面积最小点在的延长线上，的面积最大，，，，当点在线段上时，的面积最小，，，，．23．（11分）如图，抛物线的对称轴为直线，抛物线交轴于、两点，与直线交于、两点，直线与抛物线的对称轴交于点．（1）求抛物线的解析式．（2）点在直线上方的抛物线上运动，若的面积最大，求此时点的坐标．（3）在平面直角坐标系中，以点、、、为顶点的四边形是平行四边形，请直接写出符合条件点的坐标．【解答】解：（1）令，可得：，解得：，点，抛物线的对称轴为直线，，即点，，解得：，抛物线的解析式为：；（2）点在直线上方的抛物线上运动，设点，抛物线与直线交于、两点，，解得：，，点，如图，过点作轴交直线于点，点，，，当时，最大，点，；（3）当时，，点，如图，直线的解析式为，直线的解析式为，直线的解析式为，以点、、、为顶点的四边形是平行四边形，直线的解析式为，直线的解析式为，直线的解析式为，联立得，同理可得，，综上所述，符合条件的点的坐标为或或．声明：试题解析著作权属菁优网所有，未经书面同意，不得复制发布日期：2021/12/8 17:03:00；用户：星星卷大葱；邮箱：jse035@xyh.com；学号：39024125