2019-2020学年河南省新乡市长垣市九年级（上）期末数学试卷

2019-2020学年河南省新乡市长垣市九年级（上）期末数学试卷

一、选择题（每小题3分，共30分）

1．（3分）下列四个图形分别是四届国际数学家大会的会标，其中不属于中心对称图形的是　　

A． B． C． D．

2．（3分）对于函数，下列说法错误的是　　

A．它的图象分布在第一、三象限 

B．它的图象与直线无交点 

C．当时，的值随的增大而增大 

D．当时，的值随的增大而减小

3．（3分）如图，，，，是上的点，则图中与相等的角是　　

A． B． C． D．

4．（3分）若反比例函数的图象分布在二、四象限，则关于的方程的根的情况是　　

A．有两个不相等的实数根 B．有两个相等的实数根 

C．没有实数根 D．只有一个实数根

5．（3分）已知与相似且对应周长的比为，则与的面积比为　　

A． B． C． D．

6．（3分）下列说法错误的是　　

A．必然事件发生的概率是1 

B．通过大量重复试验，可以用频率估计概率 

C．概率很小的事件不可能发生 

D．投一枚图钉，“钉尖朝上”的概率不能用列举法求得

7．（3分）如果圆锥的底面半径为3，母线长为6，那么它的侧面积等于　　

A． B． C． D．

8．（3分）如图，中，，将绕点顺时针旋转得到△，点与点是对应点，边与边交于点（点不在上），则的度数为　　

A． B． C． D．

9．（3分）如图是二次函数的图象，其对称轴为，下列结论：①；②；③；④若，，，是抛物线上两点，则，其中结论正确的个数是　　

A．1个 B．2个 C．3个 D．4个

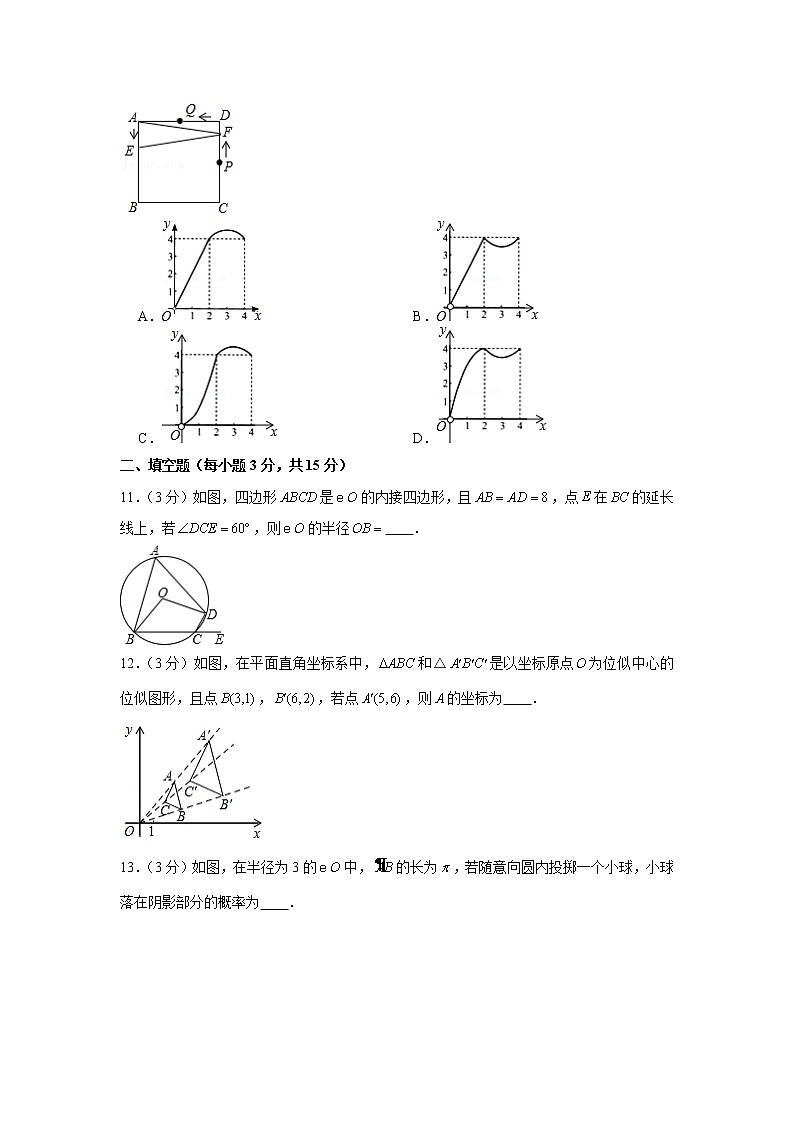
10．（3分）如图，正方形的边长为4，点、分别是、的中点，动点从点向点运动，到点时停止运动；同时，动点从点出发，沿运动，点、的运动速度相同．设点的运动路程为，的面积为，能大致刻画与的函数关系的图象是　　

A． B． 

C． D．

二、填空题（每小题3分，共15分）

11．（3分）如图，四边形是的内接四边形，且，点在的延长线上，若，则的半径　　．

12．（3分）如图，在平面直角坐标系中，和△是以坐标原点为位似中心的位似图形，且点，，若点，则的坐标为　　．

13．（3分）如图，在半径为3的中，的长为，若随意向圆内投掷一个小球，小球落在阴影部分的概率为　　．

14．（3分）一个不透明的盒子里有若干个白球，在不允许将球倒出来的情况下，为估计白球的个数，小刚向其中放入8个黑球，摇匀后从中随机摸出一个球记下颜色，再把它放回盒中，不断重复，共摸球400次，其中80次摸到黑球，估计盒中大约有白球　　个．

15．（3分）如图，在轴的正半轴上依次截取，过点、、、、分别作轴的垂线与反比例函数的图象相交于点、、、、，得直角三角形、，，，，并设其面积分别为、、、、，则　　．的整数）

三、解答题（8个小题，共75分）

16．（8分）关于的方程有实数根，且为正整数，求的值及此时方程的根．

17．（9分）为了了解班级学生数学课前预习的具体情况，郑老师对本班部分学生进行了为期一个月的跟踪调查，他将调查结果分为四类：：很好；：较好；：一般；：不达标，并将调查结果绘制成以下两幅不完整的统计图，请你根据统计图解答下列问题：

（1）类女生有　　名，类男生有　　名，将上面条形统计图补充完整；

（2）扇形统计图中“课前预习不达标”对应的圆心角度数是　　；

（3）为了共同进步，郑老师想从被调查的类和类学生中各随机抽取一位同学进行“一帮一”互助学习，请用画树状图或列表的方法求出所选两位同学恰好是一男一女同学的概率．

18．（9分）如图，在中，，且点的坐标为

（1）画出绕点逆时针旋转后的△．

（2）求点旋转到点所经过的路线长（结果保留

（3）画出关于原点对称的△

19．（9分）如图，是的直径，且，点为外一点，且，分别切于点、两点．与的延长线交于点．

（1）求证：；

（2）填空：①当　　时，四边形是正方形．

②当　　时，为等边三角形．

20．（9分）如图，在平面直角坐标系中，正比例函数的图象与反比例函数的图象经过点．

（1）分别求这两个函数的表达式；

（2）将直线向上平移3个单位长度后与轴交于，与反比例函数图象在第一象限内的交点为，连接，，求点的坐标及的面积；

21．（10分）我市某化工材料经销商购进一种化工材料若干千克，成本为每千克30元，物价部门规定其销售单价不低于成本价且不高于成本价的2倍，经试销发现，日销售量（千克）与销售单价（元符合一次函数关系，如图所示．

（1）求与之间的函数关系式，并写出自变量的取值范围；

（2）若在销售过程中每天还要支付其他费用500元，当销售单价为多少时，该公司日获利最大？最大获利是多少元？

22．（10分）在中，，，点是平面内不与点、重合的任意一点，连接，将线段绕点逆时针旋转得到线段，连接、、．

（1）观察猜想：如图（1），当时，的值是　　，直线与直线相交所成的较小角的度数是　　．

（2）类比探究：如图（2），当时，请写出的值及直线与直线相交所成的较小角的度数，并就图2的情形说明理由．

（3）解决问题：当时，若点、分别是、的中点，点在直线上，如图（3），请直接写出当点、、在同一直线上时值．

23．（11分）如图，直线与轴交于点，与轴交于点，抛物线与直线交于，两点，点是抛物线的顶点．

（1）求抛物线的解析式；

（2）点是直线上方抛物线上的一个动点，其横坐标为，过点作轴的垂线，交直线于点，当线段的长度最大时，求的值及的最大值；

（3）在抛物线上是否存在异于、的点，使中边上的高为，若存在求出点的坐标；若不存在请说明理由．

2019-2020学年河南省新乡市长垣市九年级（上）期末数学试卷

参考答案与试题解析

一、选择题（每小题3分，共30分）

1．（3分）下列四个图形分别是四届国际数学家大会的会标，其中不属于中心对称图形的是　　

A． B． C． D．

【解答】解：、不是中心对称图形，故此选项正确；

、是中心对称图形，故此选项错误；

、是中心对称图形，故此选项错误；

、是中心对称图形，故此选项错误；

故选：．

2．（3分）对于函数，下列说法错误的是　　

A．它的图象分布在第一、三象限 

B．它的图象与直线无交点 

C．当时，的值随的增大而增大 

D．当时，的值随的增大而减小

【解答】解：、函数的图象分布在第一、三象限，正确；

、将代入中，整理得：，

此方程无解，即函数的图象与直线无交点，正确；

、，

当时，的值随的增大而减小，错误；

、，

当时，的值随的增大而减小，正确．

故选：．

3．（3分）如图，，，，是上的点，则图中与相等的角是　　

A． B． C． D．

【解答】解：与都是所对的圆周角，

．

故选：．

4．（3分）若反比例函数的图象分布在二、四象限，则关于的方程的根的情况是　　

A．有两个不相等的实数根 B．有两个相等的实数根 

C．没有实数根 D．只有一个实数根

【解答】解：因为反比例函数的图象分布在二、四象限，

所以，

所以关于的方程，

△

所以关于的方程有两个不相等的实数根．

故选：．

5．（3分）已知与相似且对应周长的比为，则与的面积比为　　

A． B． C． D．

【解答】解：与相似且对应中线的比为，

两三角形的相似比等于，

．

故选：．

6．（3分）下列说法错误的是　　

A．必然事件发生的概率是1 

B．通过大量重复试验，可以用频率估计概率 

C．概率很小的事件不可能发生 

D．投一枚图钉，“钉尖朝上”的概率不能用列举法求得

【解答】解：、必然事件发生的概率是1，正确；

、通过大量重复试验，可以用频率估计概率，正确；

、概率很小的事件也有可能发生，故错误；

、投一枚图钉，“钉尖朝上”的概率不能用列举法求得，应该用频率估计概率，正确，

故选：．

7．（3分）如果圆锥的底面半径为3，母线长为6，那么它的侧面积等于　　

A． B． C． D．

【解答】解：圆锥的侧面积．

故选：．

8．（3分）如图，中，，将绕点顺时针旋转得到△，点与点是对应点，边与边交于点（点不在上），则的度数为　　

A． B． C． D．

【解答】解：根据旋转的性质可知，，

．

故选：．

9．（3分）如图是二次函数的图象，其对称轴为，下列结论：①；②；③；④若，，，是抛物线上两点，则，其中结论正确的个数是　　

A．1个 B．2个 C．3个 D．4个

【解答】解：①抛物线开口向下，对称轴为直线，与轴交于正半轴，

，，，

，

，结论①错误；

②抛物线对称轴为直线，

，

，

，结论②正确；

③抛物线的对称轴为直线，与轴的一个交点坐标是，

另一个交点坐标是，

当时，，

，结论③错误；

④，，

抛物线的对称轴为直线，抛物线开口向下，

，结论④错误；

综上所述：正确的结论有②，1个，

故选：．

10．（3分）如图，正方形的边长为4，点、分别是、的中点，动点从点向点运动，到点时停止运动；同时，动点从点出发，沿运动，点、的运动速度相同．设点的运动路程为，的面积为，能大致刻画与的函数关系的图象是　　

A． B． 

C． D．

【解答】解：当在上运动时，的面积为，

当在上运动时，的面积为，

图象为：

故选：．

二、填空题（每小题3分，共15分）

11．（3分）如图，四边形是的内接四边形，且，点在的延长线上，若，则的半径　　．

【解答】解：连接，如图所示：

四边形为的内接四边形，

，

，

，

是等边三角形，

，

作于，

则，

，，

，

，，

故答案为：．

12．（3分）如图，在平面直角坐标系中，和△是以坐标原点为位似中心的位似图形，且点，，若点，则的坐标为　　．

【解答】解：点，，点，

的坐标为：．

故答案为：．

13．（3分）如图，在半径为3的中，的长为，若随意向圆内投掷一个小球，小球落在阴影部分的概率为　　．

【解答】解：圆的面积是：，

扇形的面积是，

小球落在阴影部分的概率为；

故答案为：．

14．（3分）一个不透明的盒子里有若干个白球，在不允许将球倒出来的情况下，为估计白球的个数，小刚向其中放入8个黑球，摇匀后从中随机摸出一个球记下颜色，再把它放回盒中，不断重复，共摸球400次，其中80次摸到黑球，估计盒中大约有白球　32　个．

【解答】解；设盒子里有白球个，根据题意得：

解得：．

经检验得是方程的解．

答：盒中大约有白球32个．

故答案为：32．

15．（3分）如图，在轴的正半轴上依次截取，过点、、、、分别作轴的垂线与反比例函数的图象相交于点、、、、，得直角三角形、，，，，并设其面积分别为、、、、，则　　．的整数）

【解答】解：因为过双曲线上任意一点与原点所连的线段、坐标轴、向坐标轴作垂线所围成的直角三角形面积是个定值，．

又因为

所以，，，，

依此类推：的值为．

当时，．

故答案是：．

三、解答题（8个小题，共75分）

16．（8分）关于的方程有实数根，且为正整数，求的值及此时方程的根．

【解答】解：关于的方程有实数根，

，

解得：，

为正整数，

，

原方程可化为，

则，

解得：．

17．（9分）为了了解班级学生数学课前预习的具体情况，郑老师对本班部分学生进行了为期一个月的跟踪调查，他将调查结果分为四类：：很好；：较好；：一般；：不达标，并将调查结果绘制成以下两幅不完整的统计图，请你根据统计图解答下列问题：

（1）类女生有　3　名，类男生有　　名，将上面条形统计图补充完整；

（2）扇形统计图中“课前预习不达标”对应的圆心角度数是　　；

（3）为了共同进步，郑老师想从被调查的类和类学生中各随机抽取一位同学进行“一帮一”互助学习，请用画树状图或列表的方法求出所选两位同学恰好是一男一女同学的概率．

【解答】解：（1）类学生人数：（名

类女生人数：（名，

类学生占的百分比：，

类学生人数：（名，

类男生人数：（名，

故类女生有3名，类男生有1名；补充条形统计图，

故答案为：3，1；

（2），

答：扇形统计图中“课前预习不达标”对应的圆心角度数是；

故答案为：；

（3）由题意画树形图如下：

从树形图看出，所有可能出现的结果共有6种，且每种结果出现的可能性相等，所选

两位同学恰好是一位男同学和一位女同学的结果共有3种．

所以（所选两位同学恰好是一位男同学和一位女同学）．

18．（9分）如图，在中，，且点的坐标为

（1）画出绕点逆时针旋转后的△．

（2）求点旋转到点所经过的路线长（结果保留

（3）画出关于原点对称的△

【解答】解：（1）如图所示，△即为所求．

（2），，

点旋转到点所经过的路线长为；

（3）如图所示，△即为所求．

19．（9分）如图，是的直径，且，点为外一点，且，分别切于点、两点．与的延长线交于点．

（1）求证：；

（2）填空：①当　3　时，四边形是正方形．

②当　　时，为等边三角形．

【解答】证明：（1）如图，连接，

，分别切于点、两点，

，，，

，

是直径，

，

，，

，

，

，

（2）①四边形是正方形，

，

当时，四边形是正方形，

②若是等边三角形，

，且，，

，

，

，

当时，为等边三角形．

20．（9分）如图，在平面直角坐标系中，正比例函数的图象与反比例函数的图象经过点．

（1）分别求这两个函数的表达式；

（2）将直线向上平移3个单位长度后与轴交于，与反比例函数图象在第一象限内的交点为，连接，，求点的坐标及的面积；

【解答】解：（1）把代入得，解得；

把代入得，

正比例函数的解析式为；反比例函数的解析式为；

（2）直线向上平移3的单位得到直线的解析式为，

当时，，则，

解方程组得或，

点的坐标为；

连接，

．

21．（10分）我市某化工材料经销商购进一种化工材料若干千克，成本为每千克30元，物价部门规定其销售单价不低于成本价且不高于成本价的2倍，经试销发现，日销售量（千克）与销售单价（元符合一次函数关系，如图所示．

（1）求与之间的函数关系式，并写出自变量的取值范围；

（2）若在销售过程中每天还要支付其他费用500元，当销售单价为多少时，该公司日获利最大？最大获利是多少元？

【解答】解：（1）设一次函数关系式为，

由图象可得，当时，；时，，

，解得．

与之间的关系式为．

（2）设该公司日获利为元，由题意得，

，

抛物线开口向下；

对称轴，

当时，随着的增大而增大；

，

时，有最大值；．

即销售单价为每千克60元时，日获利最大，最大获利为1900元．

22．（10分）在中，，，点是平面内不与点、重合的任意一点，连接，将线段绕点逆时针旋转得到线段，连接、、．

（1）观察猜想：如图（1），当时，的值是　1　，直线与直线相交所成的较小角的度数是　　．

（2）类比探究：如图（2），当时，请写出的值及直线与直线相交所成的较小角的度数，并就图2的情形说明理由．

（3）解决问题：当时，若点、分别是、的中点，点在直线上，如图（3），请直接写出当点、、在同一直线上时值．

【解答】解：（1）如图1中，延长交的延长线于，设交于点．

，

，

，，

，

，，

，

，

，线与直线相交所成的较小角的度数是，

故答案为：1，．

（2）如图2中，设交于点，交于点．

，

，

，

，

，，

，

，

直线与直线相交所成的小角的度数为．

（3）如图3中，当点在线段上时，延长交的延长线于．

，，

，

，

，

，

，

，

，，

，

，

，

，

，

，

，

，

，

，，，四点共圆，

，，

，

，设，则，，

，

．

如图4中，当点在线段上时，同法可证：，设，则，，

，

，

综合以上可得的值为或．

23．（11分）如图，直线与轴交于点，与轴交于点，抛物线与直线交于，两点，点是抛物线的顶点．

（1）求抛物线的解析式；

（2）点是直线上方抛物线上的一个动点，其横坐标为，过点作轴的垂线，交直线于点，当线段的长度最大时，求的值及的最大值；

（3）在抛物线上是否存在异于、的点，使中边上的高为，若存在求出点的坐标；若不存在请说明理由．

【解答】解：（1），令，则，令，则，

故点、的坐标分别为、，

则二次函数表达式为：，将点坐标代入上式并解得：，

故抛物线的表达式为：；

（2）设点横坐标为，则，，

，

当时，有最大值；

（3）如图，过作轴交于点，交轴于点，作于，

设，则，

，

是等腰直角三角形，

，

，

当中边上的高为时，即，

，

，

当时，解得或，

或，

当时，解得或，

或，

综上可知存在满足条件的点，其坐标为，，，．

声明：试题解析著作权属菁优网所有，未经书面同意，不得复制发布

日期：2021/12/8 17:08:58；用户：星星卷大葱；邮箱：jse035@xyh.com；学号：39024125