人教版八年级上册第十二章 全等三角形综合与测试教课ppt课件

这是一份人教版八年级上册第十二章 全等三角形综合与测试教课ppt课件，共20页。PPT课件主要包含了Ⅰ连结，语言描述连结XY，连结AC，构造全等三角形，连结BD，构造两个等腰三角形，连结AD，过点D作DE⊥AB，过点E作EF⊥BC，Ⅳ中线延长一倍等内容，欢迎下载使用。
目的:构造全等三角形或等腰三角形
适用情况:图中已经存在两个点—X和Y
注意点:双添---在图形上添虚线 在证明过程中描述添法
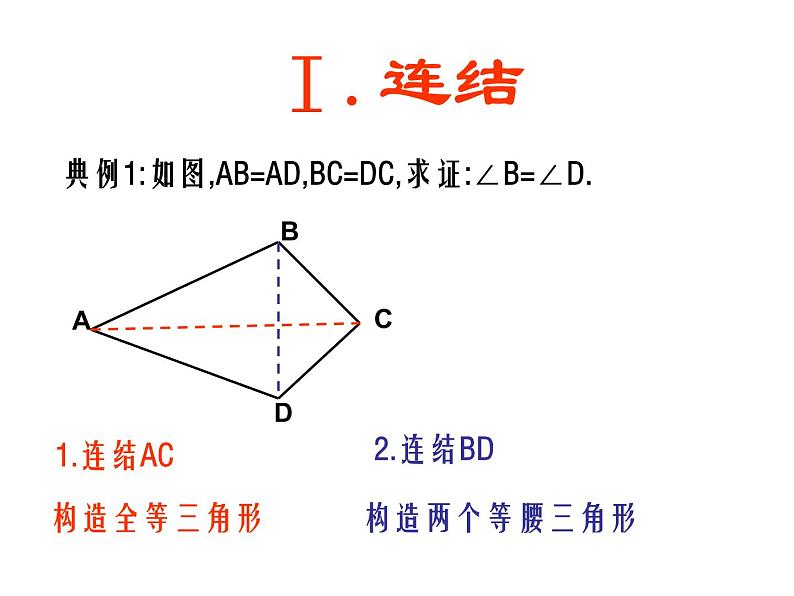
典例1:如图,AB=AD,BC=DC,求证:∠B=∠D.
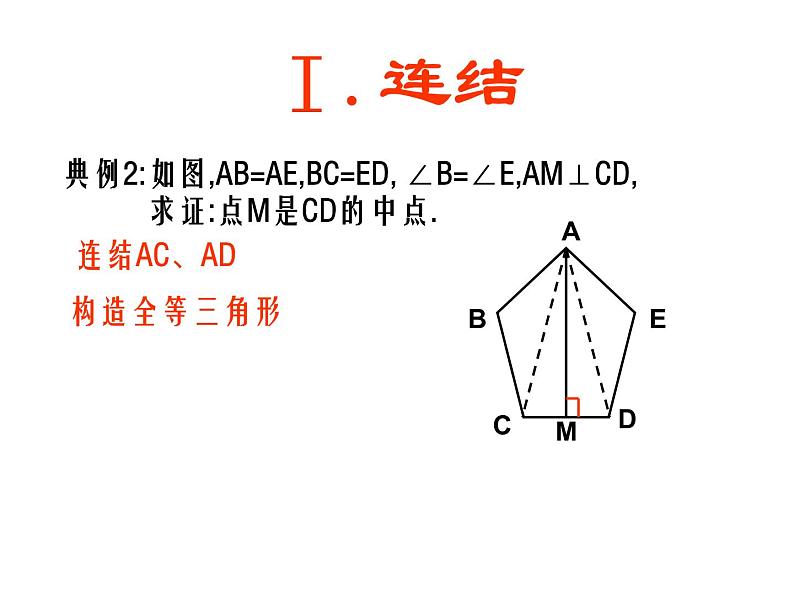
典例2:如图,AB=AE,BC=ED, ∠B=∠E,AM⊥CD, 求证:点M是CD的中点.
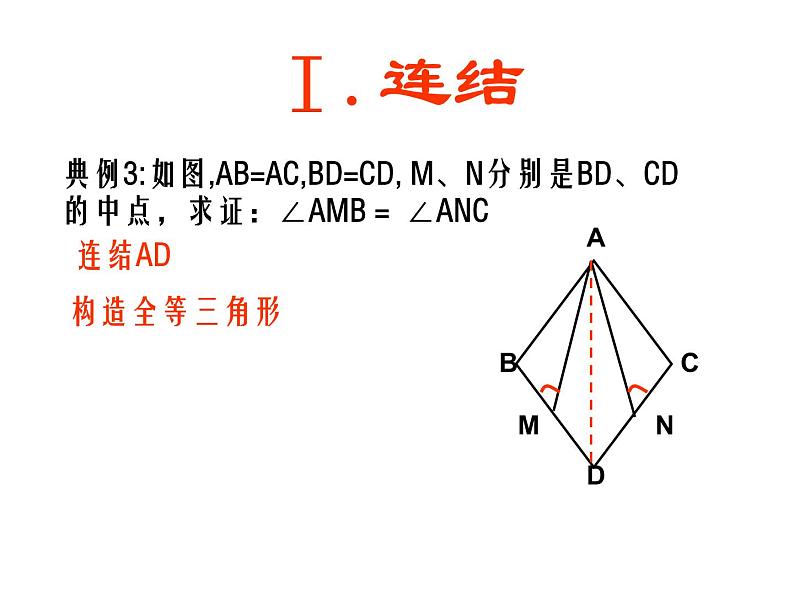
典例3:如图,AB=AC,BD=CD, M、N分别是BD、CD的中点，求证：∠AMB＝ ∠ANC
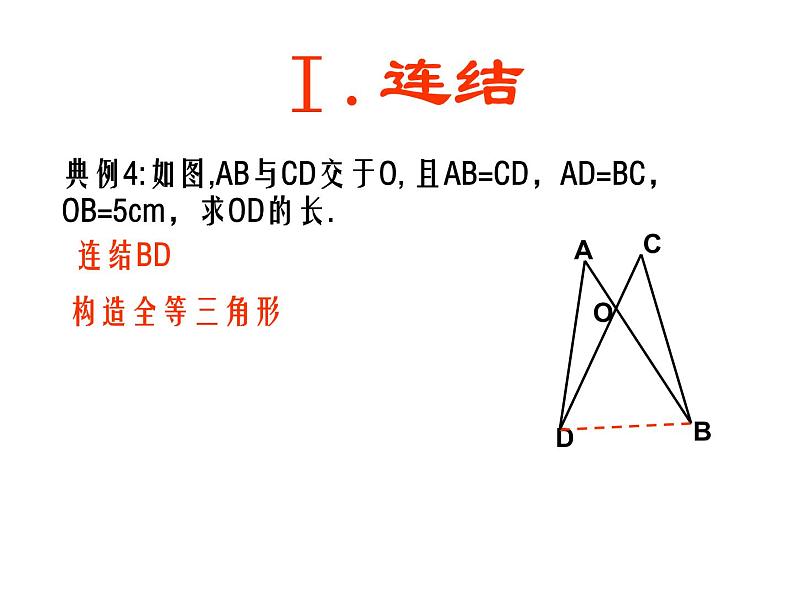
典例4:如图,AB与CD交于O, 且AB=CD，AD=BC，OB=5cm，求OD的长.
目的:构造直角三角形,得到距离相等
适用情况:图中已经存在一个点X和一条线MN
语言描述:过点X作XY⊥MN
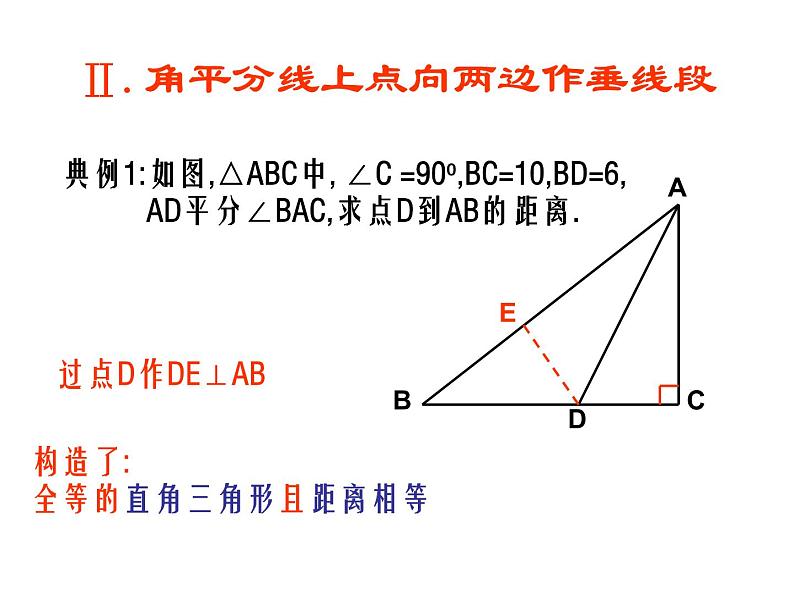
Ⅱ.角平分线上点向两边作垂线段
典例1:如图,△ABC中, ∠C =90,BC=10,BD=6, AD平分∠BAC,求点D到AB的距离.
构造了:全等的直角三角形且距离相等
典例2:如图,△ABC中, ∠C =90,AC=BC, AD平分∠BAC,求证:AB=AC+DC.
思考: 若AB=15cm,则△BED的周长是多少?
典例3:如图,梯形中, ∠A= ∠D =90, BE、CE均是角平分线, 求证:BC=AB+CD.
思考: 你从本题中还能得到哪些结论?
典例4:如图,OC 平分∠AOB, ∠DOE +∠DPE =180, 求证: PD=PE.
过点P作PF⊥OA,PG ⊥OB
目的:构造直角三角形,得到斜边相等
适用情况:图中已经存在一条线段MN 和垂直平分线上一个点X
语言描述:连结XM和XN
Ⅲ.垂直平分线上点向两端连线段
1.AD是△ABC的中线，
延长AD到点E，使DE=AE，连结CE.
2.如图,梯形中, ∠A= ∠D =90, BE、CE均是角平分线, 求证:BC=AB+CD.
延长BE和CD交于点F
构造了:全等的直角三角形
1.如图,△ABC中,∠C=90,AC=BC,AD平分∠ACB, DE⊥AB.若AB=6cm,则△DBE的周长是多少?
Ⅴ.“周长问题”的转化 借助“角平分线性质”
2.如图,△ABC中,∠C=90, D在AB的垂直平分线上,E在AC的垂直平分线上.若BC=6cm,求△ADE的周长.
Ⅴ.“周长问题”的转化 借助“垂直平分线性质”
3.如图,A、A1关于OM对称, A、A2关于ON对称.若A1 A2 =6cm,求△ABC的周长.
A1 B+ A2 C+BC
4.如图, △ABC中，MN是AC的垂直平分线.若AN=3cm, △ABM周长为13cm，求△ABC的周长.
AB+ BM+MC+6
AB+ BM+AM+6