2017-2018学年湖南省邵阳市城区九年级（上）期末数学试卷

2017-2018学年湖南省邵阳市城区九年级（上）期末数学试卷

一、选择题（30分）

1．（3分）如图，、、三点都在上，若，则的度数等于　　

A． B． C． D．

2．（3分）已知的面积为，若点到直线的距离为，则直线与的位置关系是　　

A．相交 B．相切 C．相离 D．无法确定

3．（3分）二次函数是非0常数）的图象与轴的交点个数为　　

A．0个 B．1个 C．2个 D．1个或2个

4．（3分）将抛物线向左平移2个单位，再向下平移1个单位，所得抛物线为　　

A． B． C． D．

5．（3分）已知，则下列各式中不正确的是　　

A． B． C． D．

6．（3分）已知：如图，，，以为位似中心，按比例尺  ，把缩小，则点的对应点的坐标为　　

A．或 B．或 

C． D．

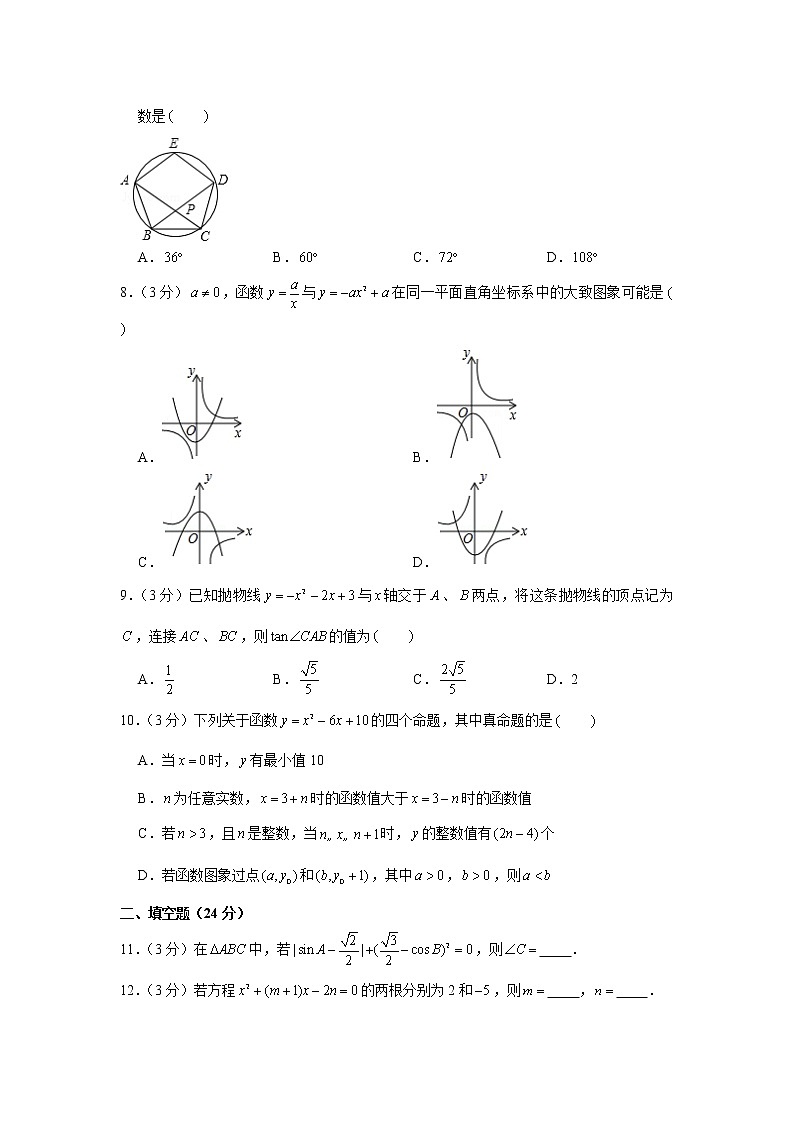
7．（3分）如图，圆内接正五边形中，对角线和相交于点，则的度数是　　

A． B． C． D．

8．（3分），函数与在同一平面直角坐标系中的大致图象可能是　　

A． B． 

C． D．

9．（3分）已知抛物线与轴交于、两点，将这条抛物线的顶点记为，连接、，则的值为　　

A． B． C． D．2

10．（3分）下列关于函数的四个命题，其中真命题的是　　

A．当时，有最小值10 

B．为任意实数，时的函数值大于时的函数值 

C．若，且是整数，当时，的整数值有个 

D．若函数图象过点和，其中，，则

二、填空题（24分）

11．（3分）在中，若，则　 　．

12．（3分）若方程的两根分别为2和，则　 　，　 　．

13．（3分）已知反比例函数的图象经过点，则的值为　　．

14．（3分）如图，将长为的铁丝首尾相接围成半径为的扇形．则　　．

15．（3分）已知二次函数的部分图象如图所示，则关于的一元二次方程的解为 　　．

16．（3分）如图，是一块锐角三角形的材料，边，高，要把它加工成正方形零件，使正方形的一边在上，其余两个顶点分别在、上，这个正方形零件的边长是　 　．

17．（3分）某地区为估计该地区黄羊的只数，先捕捉20只黄羊给它们分别作上标志，然后放回，待有标志的黄羊完全混合于黄羊群后，第二次捕捉40只黄羊，发现其中两只有标志．从而估计该地区有黄羊　 　．

18．（3分）已知等边三角形的边长为2，那么这个三角形的内切圆的半径为　 　．

三.计算题（8分）

19．（8分）（1）解方程：；

（2）计算：

四．解答题

20．（8分）如图，在中，点，分别在边，上，，射线分别交线段，于点，，且．

（1）求证：；

（2）若，求的值．

21．（8分）如图，一枚运载火箭从距雷达站处的地面处发射，当火箭到达点，时，在雷达站处测得点，的仰角分别为，，其中点，，在同一条直线上．求，两点间的距离（结果精确到．

（参考数据：，，．

22．（8分）某街道决定从备选的五种树种选购一种进行栽种，为了更好地了解社情民意，工作人员在街道辖区范围内随机抽去了部分居民，进行“我最喜欢的一种树”的调查活动（每人限选其中一种树），并将调查结果整理后，绘制成如图所示的两个不完整的统计图．

请根据所给信息解答以下问题：

（1）这次参与调查的居民人数为　 　；

（2）请将条形统计图补充完整；

（3）请计算扇形统计图中“枫树”所在扇形的圆心角度数；

（4）已知街道辖区内现有居民8万人，请估计这8万人中最喜欢玉兰树的有多少人？

23．（8分）今年某水果销售店在草莓销售旺季，试销售成本为每千克20元的草莓，规定试销期间销售单价不低于成本单价，也不高于每千克40元，经试销发现，销售量（千克）与销售单价（元符合一次函数关系，如图是与的函数关系图象．

（1）求与的函数解析式（也称关系式），请直接写出的取值范围；

（2）设该水果销售店试销草莓获得的利润为元，求的最大值．

24．（8分）如图，已知的半径为5，是的一条切线，切点为，连接并延长，交于点，过点作交于点、交于点，连接，当时，

（1）求弦的长；

（2）求证：．

25．（8分）如图，在中，，点是的中点，以为直径作分别交，于点，．连接，使四边形为的内接四边形．

（1）求证：；

（2）若，当时，求的长度；

（3）连接，，当的度数为时，求证：四边形是菱形．

26．（10分）如图，抛物线与轴交于、两点（点在点的左侧），与轴交于点，连接、．点沿以每秒1个单位长度的速度由点向点运动，同时，点沿以每秒2个单位长度的速度由点向点运动，当一个点停止运动时，另一个点也随之停止运动，连接．过点作轴，与抛物线交于点，与交于点，连接，与交于点．设点的运动时间为秒．

（1）求直线的函数表达式；

（2）①直接写出，两点的坐标（用含的代数式表示，结果需化简）

②在点、运动的过程中，当时，求的值；

（3）试探究在点，运动的过程中，是否存在某一时刻，使得点为的中点？若存在，请直接写出此时的值与点的坐标；若不存在，请说明理由．

2017-2018学年湖南省邵阳市城区九年级（上）期末数学试卷

参考答案与试题解析

一、选择题（30分）

1．（3分）如图，、、三点都在上，若，则的度数等于　　

A． B． C． D．

【解答】解：由圆周角定理，得：．故选．

2．（3分）已知的面积为，若点到直线的距离为，则直线与的位置关系是　　

A．相交 B．相切 C．相离 D．无法确定

【解答】解：设圆的半径是，

则，

，

点到直线的距离为，

，

即：，

直线与的位置关系是相离，

故选：．

3．（3分）二次函数是非0常数）的图象与轴的交点个数为　　

A．0个 B．1个 C．2个 D．1个或2个

【解答】解：二次函数是非0常数）的图象与轴的交点个数即为时方程

的解的个数，△，故图象与轴的交点个数为2个．

故选：．

4．（3分）将抛物线向左平移2个单位，再向下平移1个单位，所得抛物线为　　

A． B． C． D．

【解答】解：由“左加右减”的原则可知，将抛物线向左平移2个单位所得抛物线的解析式为：；

由“上加下减”的原则可知，将抛物线向下平移1个单位所得抛物线的解析式为：．

故选：．

5．（3分）已知，则下列各式中不正确的是　　

A． B． C． D．

【解答】解：设，．

、，正确，不符合题意；

、，正确，不符合题意；

、，正确，不符合题意；

、，不正确，符合题意．

故选：．

6．（3分）已知：如图，，，以为位似中心，按比例尺  ，把缩小，则点的对应点的坐标为　　

A．或 B．或 

C． D．

【解答】解：根据题意可知，点的对应点的坐标是的坐标同时乘以或，

所以点的坐标为或．

故选：．

7．（3分）如图，圆内接正五边形中，对角线和相交于点，则的度数是　　

A． B． C． D．

【解答】解：五边形为正五边形，

，度，

，

，

故选：．

8．（3分），函数与在同一平面直角坐标系中的大致图象可能是　　

A． B． 

C． D．

【解答】解：当时，函数的图象位于一、三象限，的开口向下，交轴的正半轴，没有符合的选项，

当时，函数的图象位于二、四象限，的开口向上，交轴的负半轴，选项符合；

故选：．

9．（3分）已知抛物线与轴交于、两点，将这条抛物线的顶点记为，连接、，则的值为　　

A． B． C． D．2

【解答】解：令，则，解得或1，不妨设，，

，

顶点，

如图所示，作于．

在中，，

故选：．

10．（3分）下列关于函数的四个命题，其中真命题的是　　

A．当时，有最小值10 

B．为任意实数，时的函数值大于时的函数值 

C．若，且是整数，当时，的整数值有个 

D．若函数图象过点和，其中，，则

【解答】解：，

当时，有最小值1，故错误；

当时，，

当时，，

，

为任意实数，时的函数值等于时的函数值，故错误；

抛物线的对称轴为，，

当时，随的增大而增大，

当时，，

当时，，

，

是整数，

是整数，

的整数值有个；故正确；

抛物线的对称轴为，，

当时，随的增大而增大，时，随的增大而减小，

，

当，时，，

当，时，，

当，时，，故错误；

故选：．

二、填空题（24分）

11．（3分）在中，若，则　　．

【解答】解：由题意，得

，，

，，

，

故答案为：

12．（3分）若方程的两根分别为2和，则　2　，　 　．

【解答】解：根据题意得，，

解得，．

故答案为2，5．

13．（3分）已知反比例函数的图象经过点，则的值为　1　．

【解答】解：反比例函数的图象经过点，

，解得．

故答案为：1．

14．（3分）如图，将长为的铁丝首尾相接围成半径为的扇形．则　4　．

【解答】解：由题意知，弧长，

扇形的面积是，

故答案为：4．

15．（3分）已知二次函数的部分图象如图所示，则关于的一元二次方程的解为 　，　．

【解答】解：根据图象可知，二次函数的部分图象经过点，所以该点适合方程，代入，得

解得①

把①代入一元二次方程，得

，②

解②得

，，

故答案为，．

16．（3分）如图，是一块锐角三角形的材料，边，高，要把它加工成正方形零件，使正方形的一边在上，其余两个顶点分别在、上，这个正方形零件的边长是　48　．

【解答】解：正方形的边在上，

，

，

．

设，

，

，

解得：，

这个正方形零件的边长是．

故答案为：48．

17．（3分）某地区为估计该地区黄羊的只数，先捕捉20只黄羊给它们分别作上标志，然后放回，待有标志的黄羊完全混合于黄羊群后，第二次捕捉40只黄羊，发现其中两只有标志．从而估计该地区有黄羊　400只　．

【解答】解：（只．

故答案为400只．

18．（3分）已知等边三角形的边长为2，那么这个三角形的内切圆的半径为　　．

【解答】解：过点作，

是等边的内心，

，

等边三角形的边长为2，

，

，

．

即这个三角形的内切圆的半径为：．

故答案为：．

三.计算题（8分）

19．（8分）（1）解方程：；

（2）计算：

【解答】解：（1），

，

，

或，

所以，；

（2）原式

．

四．解答题

20．（8分）如图，在中，点，分别在边，上，，射线分别交线段，于点，，且．

（1）求证：；

（2）若，求的值．

【解答】（1）证明：，，

．

又，

．

（2），

．

，

，

．

21．（8分）如图，一枚运载火箭从距雷达站处的地面处发射，当火箭到达点，时，在雷达站处测得点，的仰角分别为，，其中点，，在同一条直线上．求，两点间的距离（结果精确到．

（参考数据：，，．

【解答】解：由题意可得：，．

在中，

，

，

在中，，

，

，

答：，两点间的距离约为．

22．（8分）某街道决定从备选的五种树种选购一种进行栽种，为了更好地了解社情民意，工作人员在街道辖区范围内随机抽去了部分居民，进行“我最喜欢的一种树”的调查活动（每人限选其中一种树），并将调查结果整理后，绘制成如图所示的两个不完整的统计图．

请根据所给信息解答以下问题：

（1）这次参与调查的居民人数为　1000　；

（2）请将条形统计图补充完整；

（3）请计算扇形统计图中“枫树”所在扇形的圆心角度数；

（4）已知街道辖区内现有居民8万人，请估计这8万人中最喜欢玉兰树的有多少人？

【解答】解：（1）由题意可得，

这次参与调查的居民人数为：，

故答案为：1000；

（2）由题意可得，

喜欢樟树的人数为：，

补充完整的统计图图右图所示；

（3）由题意可得，

扇形统计图中“枫树”所在扇形的圆心角度数是：；

（4）由题意可得，

这8万人中最喜欢玉兰树的有：（人，

即这8万人中最喜欢玉兰树的有20000人．

23．（8分）今年某水果销售店在草莓销售旺季，试销售成本为每千克20元的草莓，规定试销期间销售单价不低于成本单价，也不高于每千克40元，经试销发现，销售量（千克）与销售单价（元符合一次函数关系，如图是与的函数关系图象．

（1）求与的函数解析式（也称关系式），请直接写出的取值范围；

（2）设该水果销售店试销草莓获得的利润为元，求的最大值．

【解答】解：（1）设与的函数解析式是，

，得，

即与的函数解析式是；

（2）由题意可得，

，

，

当时，取得最大值，此时，

答：的最大值是5200．

24．（8分）如图，已知的半径为5，是的一条切线，切点为，连接并延长，交于点，过点作交于点、交于点，连接，当时，

（1）求弦的长；

（2）求证：．

【解答】解：（1）连接，

是的切线，

，

，

，过圆心，

在中，，

，

（2），，

，

，

，

．

25．（8分）如图，在中，，点是的中点，以为直径作分别交，于点，．连接，使四边形为的内接四边形．

（1）求证：；

（2）若，当时，求的长度；

（3）连接，，当的度数为时，求证：四边形是菱形．

【解答】解：（1）证明：，点是的中点，

．

．

四边形为的内接四边形，

，

又，

．

（2）解：由（1）知，

，

．

（3）证明：由（1）知，

，

又

、都是等边三角形

，

，

四边形是平行四边形，

又

四边形是菱形

26．（10分）如图，抛物线与轴交于、两点（点在点的左侧），与轴交于点，连接、．点沿以每秒1个单位长度的速度由点向点运动，同时，点沿以每秒2个单位长度的速度由点向点运动，当一个点停止运动时，另一个点也随之停止运动，连接．过点作轴，与抛物线交于点，与交于点，连接，与交于点．设点的运动时间为秒．

（1）求直线的函数表达式；

（2）①直接写出，两点的坐标（用含的代数式表示，结果需化简）

②在点、运动的过程中，当时，求的值；

（3）试探究在点，运动的过程中，是否存在某一时刻，使得点为的中点？若存在，请直接写出此时的值与点的坐标；若不存在，请说明理由．

【解答】解：（1）由得，

解得：，，

，

由得，

，，

设直线的解析式为，，

，

直线的解析式为；

（2）①过作轴于，

，，，

．，

，

，

，

，，

，

，，

轴，，

，

，

②过作于，

则四边形是矩形，

，，，，，，，

，

解得：（舍去），，当时，的值是；

（3）点为的中点，

的横坐标为：，的纵坐标为，

，，

点在直线上，

，

解得，，

，．

声明：试题解析著作权属菁优网所有，未经书面同意，不得复制发布

日期：2021/12/2 15:14:35；用户：初中数学3；邮箱：jse034@xyh.com；学号：39024124