2019-2020学年吉林省长春市新区九年级（上）期末数学试卷

这是一份2019-2020学年吉林省长春市新区九年级（上）期末数学试卷，共27页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
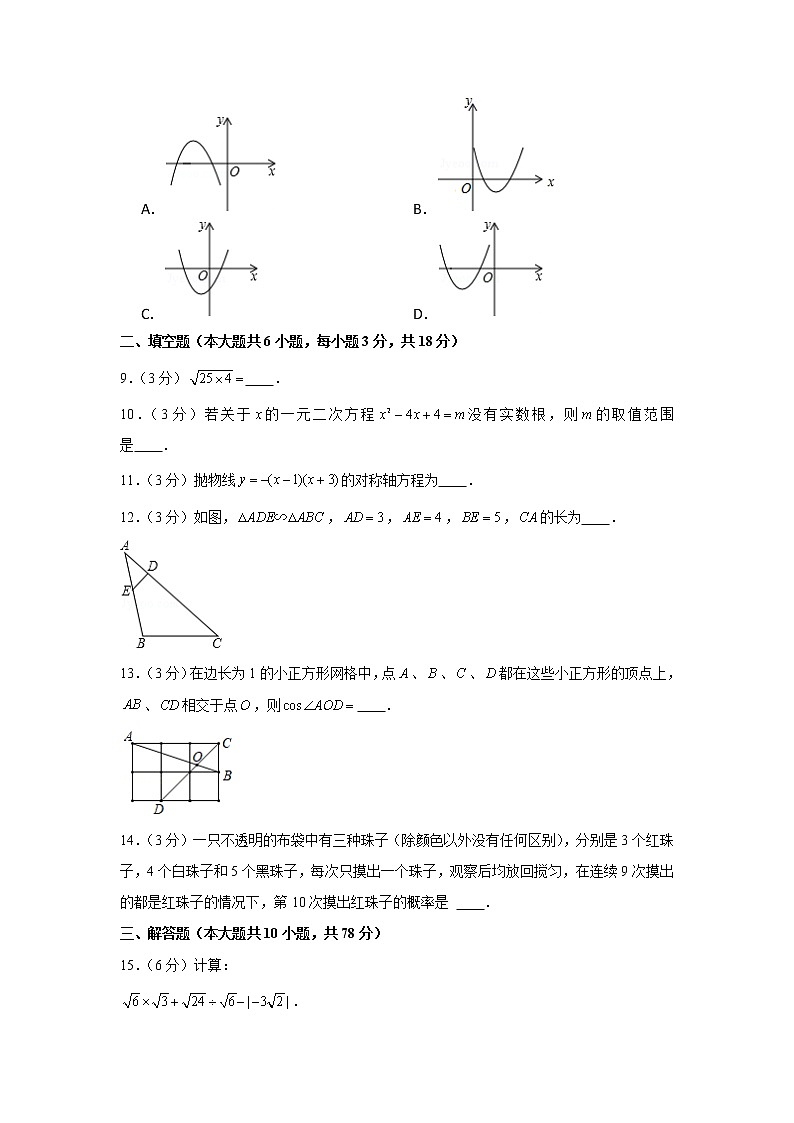
2019-2020学年吉林省长春市新区九年级（上）期末数学试卷一、选择题（本大题共8小题，每小题3分，共24分）1．（3分）下列式子中，不可以取1和2的是　　A． B． C． D．2．（3分）已知，则下列各式错误的是　　A． B． C． D．3．（3分）下列成语所描述的事件是必然事件的是　　A．守株待兔 B．拔苗助长 C．瓮中捉鳖 D．水中捞月4．（3分）已知关于的一元二次方程的一个根为0，则的值为　　A．1 B． C． D．5．（3分）用放大镜观察一个五边形时，不变的量是　　A．各边的长度 B．各内角的度数 C．五边形的周长 D．五边形的面积6．（3分）如图，已知直线，直线、与直线、、分别交于点、、、、、，，，，则　　A．7 B．7.5 C．8 D．8.57．（3分）在中，，若，，则的值为　　A． B． C． D．8．（3分）二次函数的图象大致是　　A． B． C． D．二、填空题（本大题共6小题，每小题3分，共18分）9．（3分）　　．10．（3分）若关于的一元二次方程没有实数根，则的取值范围是　　．11．（3分）抛物线的对称轴方程为　　．12．（3分）如图，，，，，的长为　　．13．（3分）在边长为1的小正方形网格中，点、、、都在这些小正方形的顶点上，、相交于点，则　　．14．（3分）一只不透明的布袋中有三种珠子（除颜色以外没有任何区别），分别是3个红珠子，4个白珠子和5个黑珠子，每次只摸出一个珠子，观察后均放回搅匀，在连续9次摸出的都是红珠子的情况下，第10次摸出红珠子的概率是 　　．三、解答题（本大题共10小题，共78分）15．（6分）计算：．16．（6分）四张大小、形状都相同的卡片上分别写有数字1，2，3，4，把它们放入不透明的盒子中摇匀．（1）从中随机抽出1张卡片，抽出的卡片上的数字恰好是偶数的概率为　　．（2）从中随机抽出1张卡片，记录数字后放回摇匀，再抽出一张卡片，记录数字．用树状图或列表法求两次抽出的卡片上的数字恰好是两个相邻整数的概率．17．（6分）某药品经过两次降价，每瓶零售价由56元降为31.5元．已知两次降价的百分比相同，求每次降价的百分率是多少．18．（7分）如图，已知是坐标原点，、两点的坐标分别为、．（1）以点为位似中心在轴的左侧将放大到两倍（即新图与原图的相似比为，画出图形；（2）点的对应点的坐标是 　　；点的对应点的坐标是 　　（3）在上有一点，按（1）的方式得到的对应点的坐标是 　　．19．（7分）在硬地上抛掷一枚图钉，通常会出现两种情况：下面是小明和同学做“抛掷图钉实验”获得的数据：抛掷次数1002003004005006007008009001000针尖不着地的频数63120186252310360434488549610针尖不着地的频率0.630.60 0.63 0.600.62 0.610.61（1）填写表中的空格；（2）画出该试验中，抛掷图钉钉尖不着地频率的折线统计图；（3）根据“抛掷图钉试验”的结果，估计“钉尖着地”的概率为 　　．20．（7分）如图①，一台灯放置在水平桌面上，底座与桌面垂直，底座高，连杆，，与始终在同一平面内．（1）如图②，转动连杆，，使成平角，，求连杆端点离桌面的高度．（2）将图②中的连杆再绕点逆时针旋转，如图③，此时连杆端点离桌面的高度减小了　　．（参考数据：，，21．（8分）利用函数图象探究方程的实数根的个数．（1）设函数，则这个函数的图象与直线的交点的横坐标就是方程的实数根．（2）分类讨论：当时，；当时，　　；（3）在给定的坐标系中，已经画出了当时的函数图象，请根据（2）中的解析式，通过描点，连线，画出当时的函数图象．（4）在给定的坐标系中画直线、观察图象可知方程的实数根有　　个．（5）深入探究：若关于的方程有三个不相等的实数根，且这三个实数根的和为负数，则的取值范围是　　．22．（9分）已知，如图，在矩形中，，，点在边上，且，以为对角线作正方形．设正方形的面积．（1）当点在矩形的边上时，　　．（2）求与的函数关系式及的取值范围．（3）当矩形的一条边将正方形的面积分为两部分时，直接写出的值．23．（10分）【知识回顾】我们把连接三角形两边中点的线段叫做三角形的中位线，并且有：三角形的中位线平行于第三边，并且等于第三边的一半．【定理证明】将下列的定理证明补充完整：已知：如图①，在中，点、分别是边、中点，连接．求证：证明：【定理应用】如图②，在中，，，点、分别是边、的中点，连接．（1）线段的长为　　．（2）以点为一个端点作线段与不平行），连接，取的中点，连接、．①在图②中补全图形．②当时，求的长．③在②的条件下，当面积最大时，直接写出的度数．24．（12分）如图，在平面直角坐标系中，线段的端点坐标分别为、．点在线段上，以为顶点的抛物线与轴交于点，与轴的一个交点为．设点的横坐标为，点的横坐标为．（1）当时，求的值．（2）求线段的长（用含的式子表示）；（3）点在轴上，设的面积为，求与的关系式；（4）当是以为直角边的直角三角形时，直接写出的值．
2019-2020学年吉林省长春市新区九年级（上）期末数学试卷参考答案与试题解析一、选择题（本大题共8小题，每小题3分，共24分）1．（3分）下列式子中，不可以取1和2的是　　A． B． C． D．【解答】解：（A）由，所以，故选项可取1和2；（B）由，所以，故选项可取1和2；（C）由，所以，故选项可取1和2；（D）由且，所以，故选项不可取1和2；故选：．2．（3分）已知，则下列各式错误的是　　A． B． C． D．【解答】解：、变成等积式是：，不符合题意；、变成等积式是：，不符合题意；、变成等积式是：，符合题意；、变成等积式是：，不符合题意．故选：．3．（3分）下列成语所描述的事件是必然事件的是　　A．守株待兔 B．拔苗助长 C．瓮中捉鳖 D．水中捞月【解答】解：、守株待兔，是随机事件，故不符合题意，、拔苗助长是不可能事件，故不符合题意；、瓮中捉鳖是必然事件，故符合题意；、水中捞月是不可能事件，故不符合题意．故选：．4．（3分）已知关于的一元二次方程的一个根为0，则的值为　　A．1 B． C． D．【解答】解：把代入方程得：，．故选：．5．（3分）用放大镜观察一个五边形时，不变的量是　　A．各边的长度 B．各内角的度数 C．五边形的周长 D．五边形的面积【解答】解：用一个放大镜去观察一个五边形，放大后的五边形与原五边形相似，相似五边形的对应边成比例，各边长都变大，故选项错误；相似五边形的对应角相等，对应角大小不变，故选项正确；相似五边形的周长得比等于相似比，选项错误．相似五边形的面积比等于相似比的平方，选项错误；故选：．6．（3分）如图，已知直线，直线、与直线、、分别交于点、、、、、，，，，则　　A．7 B．7.5 C．8 D．8.5【解答】解：，，，，，，解得：，．故选：．7．（3分）在中，，若，，则的值为　　A． B． C． D．【解答】解：如图，在中，，，，，，故选：．8．（3分）二次函数的图象大致是　　A． B． C． D．【解答】解：在中由知抛物线的开口向上，故错误；其对称轴为直线，在轴的左侧，故错误；由知抛物线与轴的交点为，在轴的负半轴，故错误；故选：．二、填空题（本大题共6小题，每小题3分，共18分）9．（3分）　10　．【解答】解：方法一：．方法二：．故答案为10．10．（3分）若关于的一元二次方程没有实数根，则的取值范围是　　．【解答】解：由题意可知：△，，故答案为：．11．（3分）抛物线的对称轴方程为　　．【解答】解：时，或，对称轴，故答案为：．12．（3分）如图，，，，，的长为　12　．【解答】解：，，，，，，解得：．故答案为：12．13．（3分）在边长为1的小正方形网格中，点、、、都在这些小正方形的顶点上，、相交于点，则　　．【解答】解：设右下角顶点为点，取的中点，连接，，如图所示．点为的中点，点为的中点，，．在中，，，，，，，．故答案为：．14．（3分）一只不透明的布袋中有三种珠子（除颜色以外没有任何区别），分别是3个红珠子，4个白珠子和5个黑珠子，每次只摸出一个珠子，观察后均放回搅匀，在连续9次摸出的都是红珠子的情况下，第10次摸出红珠子的概率是 　　．【解答】解：因为每次只摸出一个珠子时，布袋中共有珠子12个，其中红珠子3个，所以第10次摸出红珠子的概率是．故答案是：．三、解答题（本大题共10小题，共78分）15．（6分）计算：．【解答】解：原式．16．（6分）四张大小、形状都相同的卡片上分别写有数字1，2，3，4，把它们放入不透明的盒子中摇匀．（1）从中随机抽出1张卡片，抽出的卡片上的数字恰好是偶数的概率为　　．（2）从中随机抽出1张卡片，记录数字后放回摇匀，再抽出一张卡片，记录数字．用树状图或列表法求两次抽出的卡片上的数字恰好是两个相邻整数的概率．【解答】解：（1）从中随机抽出1张卡片，抽出的卡片上的数字恰好是偶数的概率；故答案为；（2）画树状图为：共有16种等可能的结果数，其中两次抽出的卡片上的数字恰好是两个相邻整数的结果数为6，所以两次抽出的卡片上的数字恰好是两个相邻整数的概率．17．（6分）某药品经过两次降价，每瓶零售价由56元降为31.5元．已知两次降价的百分比相同，求每次降价的百分率是多少．【解答】解：根据题意得：，解得：，，经检验不符合题意，则．答：每次降价百分率为．18．（7分）如图，已知是坐标原点，、两点的坐标分别为、．（1）以点为位似中心在轴的左侧将放大到两倍（即新图与原图的相似比为，画出图形；（2）点的对应点的坐标是 　　；点的对应点的坐标是 　　（3）在上有一点，按（1）的方式得到的对应点的坐标是 　　．【解答】解：（1）如图，△为所作；（2）点的对应点的坐标是；点的对应点的坐标是；（3）在上有一点，按（1）的方式得到的对应点的坐标为．故答案为：，；．19．（7分）在硬地上抛掷一枚图钉，通常会出现两种情况：下面是小明和同学做“抛掷图钉实验”获得的数据：抛掷次数1002003004005006007008009001000针尖不着地的频数63120186252310360434488549610针尖不着地的频率0.630.60 0.63 0.600.62 0.610.61（1）填写表中的空格；（2）画出该试验中，抛掷图钉钉尖不着地频率的折线统计图；（3）根据“抛掷图钉试验”的结果，估计“钉尖着地”的概率为 　0.39　．【解答】解：（1）：抛掷次数1002003004005006007008009001000针尖不着地的频数63120186252310360434488549610针尖不着地的频率0.630.600.620.630.620.600.620.610.610.61（2）（3）通过大量试验，发现频率围绕0.39上下波动，于是可以估计概率是．20．（7分）如图①，一台灯放置在水平桌面上，底座与桌面垂直，底座高，连杆，，与始终在同一平面内．（1）如图②，转动连杆，，使成平角，，求连杆端点离桌面的高度．（2）将图②中的连杆再绕点逆时针旋转，如图③，此时连杆端点离桌面的高度减小了　4　．（参考数据：，，【解答】解：（1）作于点，则，，，．四边形为矩形．，，，，，，在中，，，，，，答：连杆端点离桌面的高度为；（2）如图3，作于，于，于，于．则四边形是矩形，，，，，，，，，下降高度：．故答案为：4．21．（8分）利用函数图象探究方程的实数根的个数．（1）设函数，则这个函数的图象与直线的交点的横坐标就是方程的实数根．（2）分类讨论：当时，；当时，　　；（3）在给定的坐标系中，已经画出了当时的函数图象，请根据（2）中的解析式，通过描点，连线，画出当时的函数图象．（4）在给定的坐标系中画直线、观察图象可知方程的实数根有　　个．（5）深入探究：若关于的方程有三个不相等的实数根，且这三个实数根的和为负数，则的取值范围是　　．【解答】解：（1）函数的图象与直线的交点的横坐标就是方程的实数根．（2）当时，，故答案为；（3）如图：（4）如（3）题图，直线的图象与的图象有三个交点，则可知方程的实数根有 3个．故答案为3；（5）根据题意画出图象：直线与函数的交点的横坐标，且，，，关于的方程即有三个不相等的实数根，且这三个实数根的和为负数，则的取值范围是，故答案为．22．（9分）已知，如图，在矩形中，，，点在边上，且，以为对角线作正方形．设正方形的面积．（1）当点在矩形的边上时，　4　．（2）求与的函数关系式及的取值范围．（3）当矩形的一条边将正方形的面积分为两部分时，直接写出的值．【解答】解：（1）点在矩形的边上时，，，，，故答案为4． （2）．，． （3）①如图1中，设交于，当时，长方形的边将正方形的面积分成两部分．则，，，，，，，，． ②如图2中，设交于，当时，长方形的边将正方形的面积分成两部分．设，同法可得，，，，，，，，满足条件的的值为2或6．23．（10分）【知识回顾】我们把连接三角形两边中点的线段叫做三角形的中位线，并且有：三角形的中位线平行于第三边，并且等于第三边的一半．【定理证明】将下列的定理证明补充完整：已知：如图①，在中，点、分别是边、中点，连接．求证：证明：【定理应用】如图②，在中，，，点、分别是边、的中点，连接．（1）线段的长为　5　．（2）以点为一个端点作线段与不平行），连接，取的中点，连接、．①在图②中补全图形．②当时，求的长．③在②的条件下，当面积最大时，直接写出的度数．【解答】【定理证明】：已知：如图①，在中，点、分别是边、中点，连接．求证：，证明：、分别是、中点，，又，，，，，；【定理应用】（1）点、分别是边、的中点，，故答案为：5；（2）①补全图形②如图所示：②，，点、、分别是、、中点，，，；③由三角形的面积公式可知，当时，面积最大，如图③，，如图④，，综上所述，当面积最大时，的度数为或．24．（12分）如图，在平面直角坐标系中，线段的端点坐标分别为、．点在线段上，以为顶点的抛物线与轴交于点，与轴的一个交点为．设点的横坐标为，点的横坐标为．（1）当时，求的值．（2）求线段的长（用含的式子表示）；（3）点在轴上，设的面积为，求与的关系式；（4）当是以为直角边的直角三角形时，直接写出的值．【解答】解：（1）当时，点坐标为，抛物线表达式为．根据题意可知，抛物线表达式为．当时，，解得．由题意，；（2）点坐标为，抛物线表达式为．当时，．点坐标为，点坐标为，为；（3）如图1，延长交轴于点，，，．，，．当，即时，当，即时，综上，与的关系式为．（4）如图2，过点作，点坐标为，抛物线表达式为．当时，．点坐标为．，当时，，，，点，，，，且，，且，，，，（不合题意舍去），，如图3，过点作，同理可证，（不合题意舍去），，综上所述：当或时，是以为直角边的直角三角形．声明：试题解析著作权属菁优网所有，未经书面同意，不得复制发布日期：2021/12/12 21:39:58；用户：初中数学1；邮箱：jse032@xyh.com；学号：39024122