2019-2020学年辽宁省锦州市九年级（上）期末数学试卷

这是一份2019-2020学年辽宁省锦州市九年级（上）期末数学试卷，共26页。试卷主要包含了选择题，四象限，解答题等内容，欢迎下载使用。
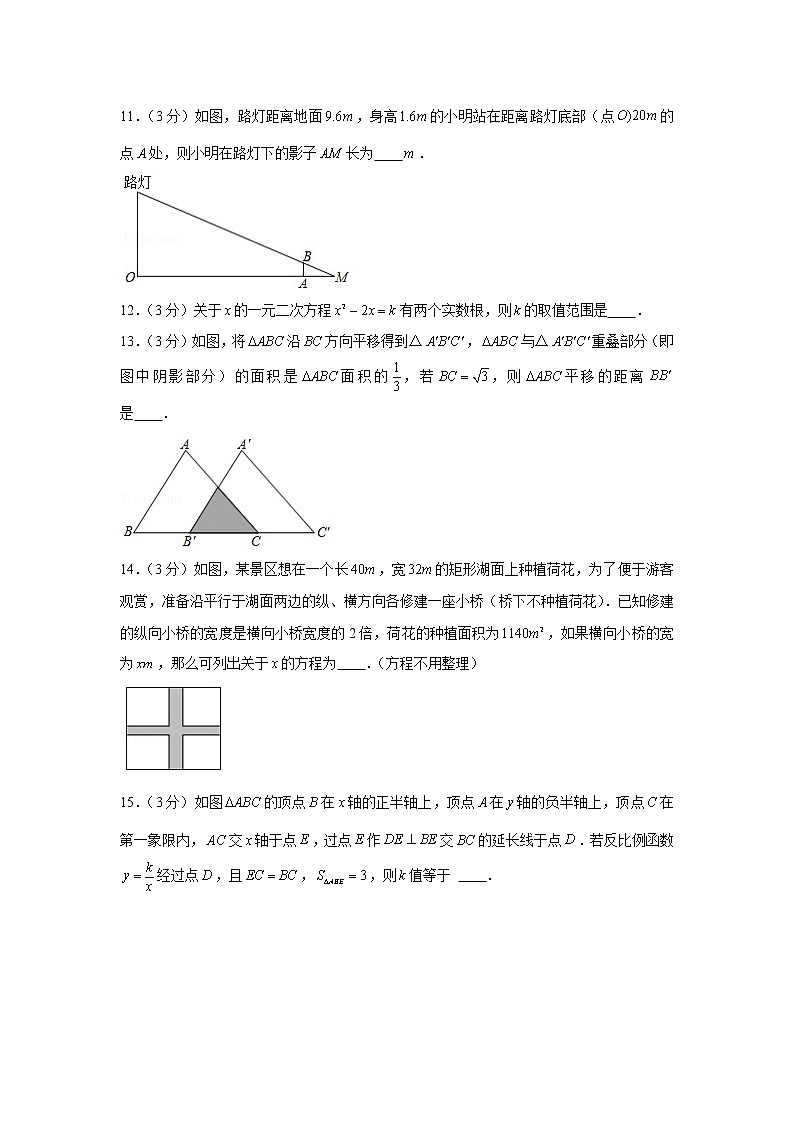
2019-2020学年辽宁省锦州市九年级（上）期末数学试卷一、选择题：本大题共8个小题，每小题2分，共16分.在每小题给出的四个选项中，只有一项是符合题目要求的.1．（2分）下列物体的光线所形成的投影是平行投影的是　　A．台灯 B．手电筒 C．太阳 D．路灯2．（2分）已知是方程的一个解，则的值是　　A． B．0 C．1 D．3．（2分）一个不透明的袋子中装有20个红球和若干个白球，这些球除了颜色外都相同，若小英每次从袋子中随机摸出一个球，记下颜色后再放回，经过多次重复试验，小英发现摸到红球的频率逐渐稳定于0.4，则小英估计袋子中白球的个数约为　　A．50 B．30 C．12 D．84．（2分）如图，已知，，，的长为　　A．4 B．6 C．8 D．105．（2分）如图，在中，，，平分，是的中点，若，则的长为　　A．4 B． C． D．6．（2分）对于反比例函数，下列说法错误的是　　A．它的图象分别位于第二、四象限 B．它的图象关于成轴对称 C．若点，在该函数图象上，则 D．的值随值的增大而减小7．（2分）如图，在菱形中，，是线段上一动点（点不与点，重合），当是等腰三角形时，　　A． B． C．或 D．或8．（2分）如图，在正方形中，，分别为，的中点，，交于点，连接，则　　A． B． C． D．二、填空题（本题共8小题，每题3分，满分24分）9．（3分）如图，已知菱形的面积为，的长为，则的长为　　．10．（3分）从一副扑克牌中取出两张红桃和两张黑桃，将这四张扑克牌洗匀后背面朝上，从中随机摸出两张牌，那么摸到两张都是红牌的概率是　　．11．（3分）如图，路灯距离地面，身高的小明站在距离路灯底部（点的点处，则小明在路灯下的影子长为　　．12．（3分）关于的一元二次方程有两个实数根，则的取值范围是　　．13．（3分）如图，将沿方向平移得到△，与△重叠部分（即图中阴影部分）的面积是面积的，若，则平移的距离是　　．14．（3分）如图，某景区想在一个长，宽的矩形湖面上种植荷花，为了便于游客观赏，准备沿平行于湖面两边的纵、横方向各修建一座小桥（桥下不种植荷花）．已知修建的纵向小桥的宽度是横向小桥宽度的2倍，荷花的种植面积为，如果横向小桥的宽为，那么可列出关于的方程为　　．（方程不用整理）15．（3分）如图的顶点在轴的正半轴上，顶点在轴的负半轴上，顶点在第一象限内，交轴于点，过点作交的延长线于点．若反比例函数经过点，且，，则值等于 　　．16．（3分）如图，已知直线，点，过点作轴的垂线交直线于点，以为边，向右侧作正方形，延长交直线于点；以为边，向右侧作正方形，延长交直线于点；以为边，向右侧作正方形，延长交直线于点；；按照这个规律进行下去，点的横坐标为　　．（结果用含正整数的代数式表示）三、解答题（本大题共3小题，17题8分，18，19题各6分，共20分.）17．（8分）用适当的方法解下列一元二次方程：（1）；（2）．18．（6分）如图，在平面直角坐标系中，已知三个顶点的坐标分别是，，．（1）请画出关于轴对称的△；（2）以点为位似中心，相似比为，在轴右侧，画出△放大后的△；19．（6分）画出如图所示的几何体的主视图、左视图和俯视图．四、解答题（本大题共2小题，媒体7分，共14分）20．（7分）为了“城市更美好、人民更幸福”，我市开展“三城联创”活动，环卫部门要求垃圾按，，三类分别装袋、投放，其中类指废电池，过期药品等有毒垃圾，类指剩余食品等厨余垃圾，类指塑料、废纸等可回收垃圾，甲、乙两人各投放一袋垃圾．（1）甲投放的垃圾恰好是类的概率是　　；（2）用树状图或表格求甲、乙两人投放的垃圾是不同类别的概率．21．（7分）如图，在中，，，以为顶点在边上方作菱形，使点，分别在，边上，另两边，分别交于点，，且点恰好平分．（1）求证：；（2）请说明：．五、解答题（本大题共3小题，22，23题各8分，24题10分，共26分）22．（8分）为促进新旧功能转换，提高经济效益，某科技公司近期研发出一种新型高科技设备，每台设备成本价为25万元，经过市场调研发现，该设备的月销售量（台和销售单价（万元）满足如图所示的一次函数关系．（1）求月销售量与销售单价的函数关系式；（2）根据相关规定，此设备的销售单价不得高于35万元，如果该公司想获得130万元的月利润，那么该设备的销售单价应是多少万元？23．（8分）如图，在平面直角坐标系中，矩形的顶点，分别在轴和轴的正半轴上，顶点的坐标为，的垂直平分线分别交，于点，，过点的反比例函数的图象交于点．（1）求反比例函数的表示式；（2）判断与的位置关系，并说明理由；（3）连接，在反比例函数图象上存在点，使，直接写出点的坐标．24．（10分）如图1，是内任意一点，连接，，分别以，为边作在的左侧）和在的右侧），使得，，连接，．（1）求证：；（2）如图2，，交于点，若，点，，共线，其他条件不变，①判断四边形的形状，并说明理由；②当，，且四边形是正方形时，直接写出的长．
2019-2020学年辽宁省锦州市九年级（上）期末数学试卷参考答案与试题解析一、选择题：本大题共8个小题，每小题2分，共16分.在每小题给出的四个选项中，只有一项是符合题目要求的.1．（2分）下列物体的光线所形成的投影是平行投影的是　　A．台灯 B．手电筒 C．太阳 D．路灯【解答】解：太阳光线所形成的投影是平行投影，故选：．2．（2分）已知是方程的一个解，则的值是　　A． B．0 C．1 D．【解答】解：把代入方程得，解得．故选：．3．（2分）一个不透明的袋子中装有20个红球和若干个白球，这些球除了颜色外都相同，若小英每次从袋子中随机摸出一个球，记下颜色后再放回，经过多次重复试验，小英发现摸到红球的频率逐渐稳定于0.4，则小英估计袋子中白球的个数约为　　A．50 B．30 C．12 D．8【解答】解：设袋中白球有个，根据题意，得：，解得：，经检验：是分式方程的解，所以小英估计袋子中白球的个数约为30个，故选：．4．（2分）如图，已知，，，的长为　　A．4 B．6 C．8 D．10【解答】解：，，即，，故选：．5．（2分）如图，在中，，，平分，是的中点，若，则的长为　　A．4 B． C． D．【解答】解：在中，，，，，平分，，在中，，，是的中点，，故选：．6．（2分）对于反比例函数，下列说法错误的是　　A．它的图象分别位于第二、四象限 B．它的图象关于成轴对称 C．若点，在该函数图象上，则 D．的值随值的增大而减小【解答】解：、反比例函数中，，此函数图象在二、四象限，故本选项正确，不符合题意；、反比例函数的图象双曲线成轴对称，故本选项正确，不符合题意；、反比例函数，若点，在该函数图象上，则，故本选项正确，不符合题意；、反比例函数，的图象在二、四象限，在每一象限内，随的增大而增大，故本选项错误，符合题意．故选：．7．（2分）如图，在菱形中，，是线段上一动点（点不与点，重合），当是等腰三角形时，　　A． B． C．或 D．或【解答】解：在菱形中，，，，，是等腰三角形，，或，当时，，；当时，，，综上所述，当是等腰三角形时，或，故选：．8．（2分）如图，在正方形中，，分别为，的中点，，交于点，连接，则　　A． B． C． D．【解答】解：延长、交于，在和中，，，，．，，，，．故选：．二、填空题（本题共8小题，每题3分，满分24分）9．（3分）如图，已知菱形的面积为，的长为，则的长为　3　．【解答】解：菱形的面积为，的长为，，解得：，故答案为：3．10．（3分）从一副扑克牌中取出两张红桃和两张黑桃，将这四张扑克牌洗匀后背面朝上，从中随机摸出两张牌，那么摸到两张都是红牌的概率是　　．【解答】解：根据题意画图如下：共有12中情况，从4张牌中任意摸出两张都是红牌有2种可能，所以两张都是红牌概率，故答案为：．11．（3分）如图，路灯距离地面，身高的小明站在距离路灯底部（点的点处，则小明在路灯下的影子长为　4　．【解答】解：由题意得，，即，解得：．故答案为：4．12．（3分）关于的一元二次方程有两个实数根，则的取值范围是　　．【解答】解：原方程可变形为．方程有两个实数根，△，解得：．故答案为：．13．（3分）如图，将沿方向平移得到△，与△重叠部分（即图中阴影部分）的面积是面积的，若，则平移的距离是　　．【解答】解：如图，设与相交于点，根据平移的性质，，△，重叠部分（图中阴影部分）的面积是的，，，，．故答案为：．14．（3分）如图，某景区想在一个长，宽的矩形湖面上种植荷花，为了便于游客观赏，准备沿平行于湖面两边的纵、横方向各修建一座小桥（桥下不种植荷花）．已知修建的纵向小桥的宽度是横向小桥宽度的2倍，荷花的种植面积为，如果横向小桥的宽为，那么可列出关于的方程为　　．（方程不用整理）【解答】解：设横向小桥的宽为，依题意得：，故答案为：．15．（3分）如图的顶点在轴的正半轴上，顶点在轴的负半轴上，顶点在第一象限内，交轴于点，过点作交的延长线于点．若反比例函数经过点，且，，则值等于 　6　．【解答】解：过点作于点，如图：点为线段的中点设点，，则，，，，，，，即，即；故答案为：6．16．（3分）如图，已知直线，点，过点作轴的垂线交直线于点，以为边，向右侧作正方形，延长交直线于点；以为边，向右侧作正方形，延长交直线于点；以为边，向右侧作正方形，延长交直线于点；；按照这个规律进行下去，点的横坐标为　　．（结果用含正整数的代数式表示）【解答】解：直线，点坐标为，过点作轴的垂线交直线于点，可知点的坐标为，以 为边作正方形，，，点的坐标为，的横坐标为3，这种方法可求得的坐标为，故点的坐标为，，的横坐标为，此类推便可求出点点的坐标为，，点的横坐标为．故答案为．三、解答题（本大题共3小题，17题8分，18，19题各6分，共20分.）17．（8分）用适当的方法解下列一元二次方程：（1）；（2）．【解答】解：（1）原方程变形，即．或．．（2），，．18．（6分）如图，在平面直角坐标系中，已知三个顶点的坐标分别是，，．（1）请画出关于轴对称的△；（2）以点为位似中心，相似比为，在轴右侧，画出△放大后的△；【解答】解：（1）如图所示：△即为所求．（2）如图所示，△即为所求．19．（6分）画出如图所示的几何体的主视图、左视图和俯视图．【解答】解：该几何体的主视图、左视图和俯视图，如图所示：四、解答题（本大题共2小题，媒体7分，共14分）20．（7分）为了“城市更美好、人民更幸福”，我市开展“三城联创”活动，环卫部门要求垃圾按，，三类分别装袋、投放，其中类指废电池，过期药品等有毒垃圾，类指剩余食品等厨余垃圾，类指塑料、废纸等可回收垃圾，甲、乙两人各投放一袋垃圾．（1）甲投放的垃圾恰好是类的概率是　　；（2）用树状图或表格求甲、乙两人投放的垃圾是不同类别的概率．【解答】解：（1）垃圾要按，，三类分别装袋，甲投放了一袋垃圾，甲投放的垃圾恰好是类的概率为：，故答案为：；（2）甲乙由表格可知，甲、乙两人投放的垃圾共有9种结果，每种结果出现的可能性相同，其中甲、乙投放的垃圾恰是不同类别的有6种，即，，，，，，（甲、乙投放的垃圾是不同类别）．21．（7分）如图，在中，，，以为顶点在边上方作菱形，使点，分别在，边上，另两边，分别交于点，，且点恰好平分．（1）求证：；（2）请说明：．【解答】解：（1）连接，，，．四边形是菱形，，，是等边三角形．是的中点，（2），．．，．．．．．．．五、解答题（本大题共3小题，22，23题各8分，24题10分，共26分）22．（8分）为促进新旧功能转换，提高经济效益，某科技公司近期研发出一种新型高科技设备，每台设备成本价为25万元，经过市场调研发现，该设备的月销售量（台和销售单价（万元）满足如图所示的一次函数关系．（1）求月销售量与销售单价的函数关系式；（2）根据相关规定，此设备的销售单价不得高于35万元，如果该公司想获得130万元的月利润，那么该设备的销售单价应是多少万元？【解答】解：（1）设与的函数关系式为，依题意，得解得所以与的函数关系式为．（2）依题知．整理方程，得．解得，．此设备的销售单价不得高于35万元，（舍，所以．答：该设备的销售单价应是27 万元．23．（8分）如图，在平面直角坐标系中，矩形的顶点，分别在轴和轴的正半轴上，顶点的坐标为，的垂直平分线分别交，于点，，过点的反比例函数的图象交于点．（1）求反比例函数的表示式；（2）判断与的位置关系，并说明理由；（3）连接，在反比例函数图象上存在点，使，直接写出点的坐标．【解答】解：（1）连接，垂直平分，，，，．设，则，四边形矩形，，．在中，．即．解得．点．将点的坐标代入中，解得：．所求反比例函数表达式为；（2）．将代入得，，点．，，，，，，，．，．．，，．；（3）存在，，，，如图，点在反比例函数图象上，设，过作于，，，，，，，，，，解得：，（不合题意舍去），．24．（10分）如图1，是内任意一点，连接，，分别以，为边作在的左侧）和在的右侧），使得，，连接，．（1）求证：；（2）如图2，，交于点，若，点，，共线，其他条件不变，①判断四边形的形状，并说明理由；②当，，且四边形是正方形时，直接写出的长．【解答】解：（1），，．，，即．．；（2）①四边形是矩形．理由如下：由（1）知，，．，．．．，，，，，即．，．，．，，．四边形是平行四边形；，，点，，共线，．四边形是矩形；②，，，，，，，设，，四边形是正方形，，，，，，，，，（负值舍去），．声明：试题解析著作权属菁优网所有，未经书面同意，不得复制发布日期：2021/12/10 10:48:28；用户：星星卷大葱；邮箱：jse035@xyh.com；学号：39024125