2020-2021学年内蒙古呼和浩特市九年级（上）期末数学试卷

这是一份2020-2021学年内蒙古呼和浩特市九年级（上）期末数学试卷，共24页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
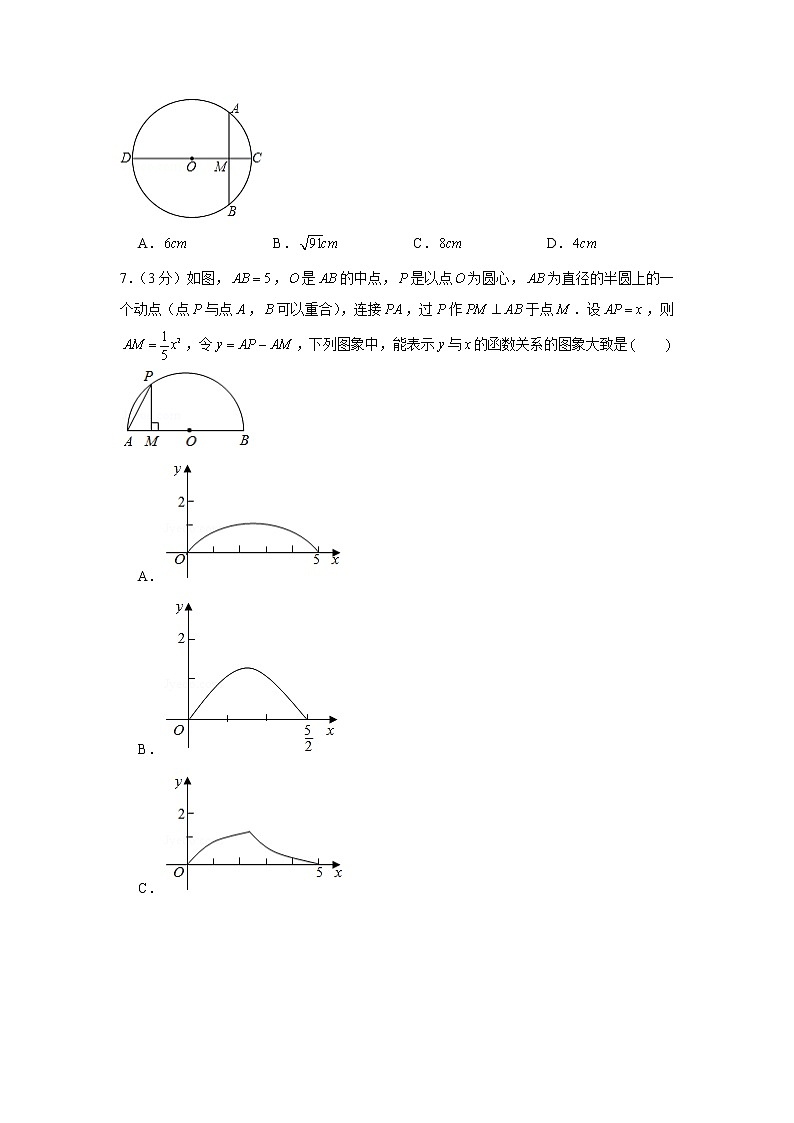
2020-2021学年内蒙古呼和浩特市九年级（上）期末数学试卷一、选择题（本大题共10小题，共25分。1-5题每题2分，6-10小题每题3分.在每小题给出的四个选项中，只有一项是符合题目要求的）1．（2分）下列事件是必然事件的是　　A．经过有交通信号灯的路口，遇到红灯 B．射击运动员射击一次，命中靶心 C．从一定高度落下的图钉，落地后钉尖朝下 D．标准大气压下温度降到以下，纯净的水会结冰2．（2分）把点绕原点顺时针旋转，点的对应点的坐标是　　A． B． C． D．3．（2分）如图，，是的切线，，为切点，是的直径，，则的度数为　　A． B． C． D．4．（2分）函数的图象上的点一定在第　　象限．A．第一象限 B．第二象限 C．第三象限 D．第四象限5．（2分）半径为2的圆内接正六边形的边心距的长是　　A．2 B．1 C． D．6．（3分）如图，的直径，是的弦，，垂足为，，则的长为　　A． B． C． D．7．（3分）如图，，是的中点，是以点为圆心，为直径的半圆上的一个动点（点与点，可以重合），连接，过作于点．设，则，令，下列图象中，能表示与的函数关系的图象大致是　　A． B． C． D．8．（3分）已知二次函数，当取互为相反数的任意两个实数值时，对应的函数值总相等，则关于的一元二次方程的两根之积为　　A． B． C． D．09．（3分）用一个圆心角为，半径为4的扇形，做一个圆锥的侧面，则这个圆锥的全面积（侧面与底面面积的和）为　　A． B． C． D．10．（3分）下列结论中：①的内切圆半径为，的周长为，则的面积是；②同时抛掷两枚质地均匀的硬币，两枚硬币全部正面向上的概率为；③圆内接平行四边形是矩形；④无论取何值，方程总有两个不等的实数根．其中正确的结论有　　A．4个 B．3个 C．2个 D．1个二、填空题（本大题共10小题，其中11-14每小题2分，15-20小题每题3分.共26分.本题要求把正确结果填在规定的横线上，不需要解答过程。）11．（2分）把一枚质地均匀的骰子先后抛掷两次，将“两次抛掷骰子所得点数相同”记为事件，则（A）　　．12．（2分）如图，四边形内接于，若，则的度数是　　．13．（2分）关于的方程的实数根为　　．14．（2分）已知二次函数的图象如图所示，则时，对应的的取值范围为　　．15．（3分）在设计人体雕像时，使雕像的上部（腰以上）与下部（腰以下）的高度比，等于下部与全部（全身）的高度比，可以增加视觉美感．按此比例，如果雕像的高为，设雕像下部高为，则可得到方程　　．16．（3分）已知，，是抛物线上的点，则，，的大小关系是　　．17．（3分）如图，已知电流在一定时间段内正常通过电子元件“”的概率是，在一定时间段内，，之间电流能够正常通过的概率为　　．18．（3分）下列四个二次函数：①，②，③，④，其中抛物线开口按从大到小的顺序排列是　　．19．（3分）下列说法中正确的说法的序号是　　．①367人中至少有两人是同月同日生；②某商场抽奖活动的中奖率为1‰，说明每抽1000张奖券，一定有一张能中奖；③“打开电视机，正在播放《动物世界》”是随机事件；④“明天降雨的概率是”表示明天有的时间降雨．20．（3分）二次函数的图象如图，对称轴为直线．若关于的一元二次方程为实数）在的范围内有解，则的取值范围是 　　．三、解答题（本大题共7小题，共69分.解答应写出文字说明计算过程或演算步骤）21．（12分）按要求解下列方程：（1）（配方法）；（2）（因式分解法）．22．（7分）如图，在平面直角坐标系内顶点的坐标分别为，，．（1）平移，使点移到点，画出平移后的△，并写出点，的坐标；（2）画出与关于原点对称的图形．23．（8分）已知关于的一元二次方程．（1）求证：当时，方程一定有两个不相等的实数根；（2）已知是它的一个实数根，若，求的值．24．（10分）如图1所示，将一个边长为2的正方形和一个长为2、宽为1的长方形拼在一起，构成一个大的长方形．现将小长方形绕点顺时针旋转至，旋转角为．（1）当点恰好落在边上时，求旋转角的值；（2）如图2，为中点，且，求证：；（3）小长方形绕点顺时针旋转一周的过程中，与能否全等？若能，直接写出旋转角的值；若不能说明理由．25．（10分）已知二次函数．（1）求证：当时，任意实数，对应的函数值；（2）该函数图象是否可以通过函数的图象平移得到，如果能，请写出变化过程．26．（10分）如图，是半圆的直径，点是半圆上不同于，的一动点，在弧上取点，使，为半圆的切线，过点作于点．（1）求证：；（2）连接，．探究：当等于多少度时，四边形为菱形，并且写出证明过程．27．（12分）我市某乡镇在“精准扶贫”活动中销售一农产品，经分析发现月销售量（万件）与月份（月的关系为：，每件产品的利润（元与月份（月的关系如下表：123456789101112191817161514131211101010（1）请你根据表格求出每件产品利润（元与月份（月的关系式；（2）若月利润（万元）当月销售量（万件）当月每件产品的利润（元，求月利润（万元）与月份（月的关系式；（3）当为何值时，月利润有最大值，最大值为多少？
2020-2021学年内蒙古呼和浩特市九年级（上）期末数学试卷参考答案与试题解析一、选择题（本大题共10小题，共25分。1-5题每题2分，6-10小题每题3分.在每小题给出的四个选项中，只有一项是符合题目要求的）1．（2分）下列事件是必然事件的是　　A．经过有交通信号灯的路口，遇到红灯 B．射击运动员射击一次，命中靶心 C．从一定高度落下的图钉，落地后钉尖朝下 D．标准大气压下温度降到以下，纯净的水会结冰【解答】解：、经过有交通信号灯的路口，遇到红灯，是随机事件；、射击运动员射击一次，命中靶心，是随机事件；、从一定高度落下的图钉，落地后钉尖朝下，是随机事件；、标准大气压下温度降到以下，纯净的水会结冰，是必然事件；故选：．2．（2分）把点绕原点顺时针旋转，点的对应点的坐标是　　A． B． C． D．【解答】解：如图，不妨设点在第一象限，作轴于，轴于．点是由点绕顺时针旋转得到，，，，，，在和△中，，△，，，．故选：．3．（2分）如图，，是的切线，，为切点，是的直径，，则的度数为　　A． B． C． D．【解答】解：是的直径，是的切线，，，，是的切线，，，，故选：．4．（2分）函数的图象上的点一定在第　　象限．A．第一象限 B．第二象限 C．第三象限 D．第四象限【解答】解：，，，，，点一定在第二象限．故选：．5．（2分）半径为2的圆内接正六边形的边心距的长是　　A．2 B．1 C． D．【解答】解：边长为2的正六边形可以分成六个边长为2的正三角形，而正多边形的边心距即为每个边长为2的正三角形的高，正六多边形的边心距等于，故选：．6．（3分）如图，的直径，是的弦，，垂足为，，则的长为　　A． B． C． D．【解答】解：，，，，，，连接，如图，在中，，．故选：．7．（3分）如图，，是的中点，是以点为圆心，为直径的半圆上的一个动点（点与点，可以重合），连接，过作于点．设，则，令，下列图象中，能表示与的函数关系的图象大致是　　A． B． C． D．【解答】解：由题意得：，，故抛物线开口向下，当时，的最大值为，故选：．8．（3分）已知二次函数，当取互为相反数的任意两个实数值时，对应的函数值总相等，则关于的一元二次方程的两根之积为　　A． B． C． D．0【解答】解：二次函数，当取互为相反数的任意两个实数值时，对应的函数值总相等，该函数的对称轴为直线，解得，二次函数，当时，，解得，，一元二次方程的两根是，，一元二次方程的两根之积是，故选：．9．（3分）用一个圆心角为，半径为4的扇形，做一个圆锥的侧面，则这个圆锥的全面积（侧面与底面面积的和）为　　A． B． C． D．【解答】解：设圆锥的底面圆的半径为，根据题意得，解得，所以这个圆锥的全面积．故选：．10．（3分）下列结论中：①的内切圆半径为，的周长为，则的面积是；②同时抛掷两枚质地均匀的硬币，两枚硬币全部正面向上的概率为；③圆内接平行四边形是矩形；④无论取何值，方程总有两个不等的实数根．其中正确的结论有　　A．4个 B．3个 C．2个 D．1个【解答】解：①的内切圆半径为，的周长为，则的面积是，故①正确；②同时抛掷两枚质地均匀的硬币，两枚硬币全部正面向上的概率为，故②错误；③圆内接平行四边形是矩形；故③正确；④方程，△，无论取何值，总有两个不等的实数根．故④正确；故选：．二、填空题（本大题共10小题，其中11-14每小题2分，15-20小题每题3分.共26分.本题要求把正确结果填在规定的横线上，不需要解答过程。）11．（2分）把一枚质地均匀的骰子先后抛掷两次，将“两次抛掷骰子所得点数相同”记为事件，则（A）　　．【解答】解：利用列表法表示所有可能出现的结果如下：共有36种等可能出现的结果，其中“两次抛掷骰子所得点数相同”的有6种，，故答案为：．12．（2分）如图，四边形内接于，若，则的度数是　　．【解答】解：四边形内接于，，故答案为：．13．（2分）关于的方程的实数根为　，　．【解答】解：，，则或，解得，，故答案为：，．14．（2分）已知二次函数的图象如图所示，则时，对应的的取值范围为　或　．【解答】解：由图象可知，当时，的取值范围是或，故答案是：或．15．（3分）在设计人体雕像时，使雕像的上部（腰以上）与下部（腰以下）的高度比，等于下部与全部（全身）的高度比，可以增加视觉美感．按此比例，如果雕像的高为，设雕像下部高为，则可得到方程　　．【解答】解：根据题意得：，整理得：，故答案为：．16．（3分）已知，，是抛物线上的点，则，，的大小关系是　　．【解答】解：抛物线的开口向下，对称轴是直线，当时，随的增大而增大，，，是抛物线上的点，点关于对称轴的对称点是，，，故答案为．17．（3分）如图，已知电流在一定时间段内正常通过电子元件“”的概率是，在一定时间段内，，之间电流能够正常通过的概率为　　．【解答】解：根据题意，电流在一定时间段内正常通过电子元件的概率是0.5，即某一个电子元件不正常工作的概率为，则两个元件同时不正常工作的概率为；故在一定时间段内之间电流能够正常通过的概率为；故答案为：．18．（3分）下列四个二次函数：①，②，③，④，其中抛物线开口按从大到小的顺序排列是　③①②④　．【解答】解：，抛物线开口按从大到小的顺序排列是③①②④，故答案为：③①②④．19．（3分）下列说法中正确的说法的序号是　①③　．①367人中至少有两人是同月同日生；②某商场抽奖活动的中奖率为1‰，说明每抽1000张奖券，一定有一张能中奖；③“打开电视机，正在播放《动物世界》”是随机事件；④“明天降雨的概率是”表示明天有的时间降雨．【解答】解：①367人中至少有两人是同月同日生，正确；②某商场抽奖活动的中奖率为1‰，是随机事件，不一定每抽1000张奖券，一定有一张能中奖，故本选项错误；③“打开电视机，正在播放《动物世界》”是随机事件，正确；④、“明天降雨的概率是”表示明天降雨的可能性大，但不一定是明天有的时间降雨，故本选项错误；则说法中正确的是①③．故答案为：①③．20．（3分）二次函数的图象如图，对称轴为直线．若关于的一元二次方程为实数）在的范围内有解，则的取值范围是 　．　．【解答】解：对称轴为直线，，二次函数解析式为．当时，；当时，；当时，．相当于与直线的交点的横坐标，当时，在的范围内有解．故答案为：．三、解答题（本大题共7小题，共69分.解答应写出文字说明计算过程或演算步骤）21．（12分）按要求解下列方程：（1）（配方法）；（2）（因式分解法）．【解答】解：（1）．，配方得：，即，开方得：，原方程的解是：，．（2）．，因式分解得，或，，．22．（7分）如图，在平面直角坐标系内顶点的坐标分别为，，．（1）平移，使点移到点，画出平移后的△，并写出点，的坐标；（2）画出与关于原点对称的图形．【解答】解：（1）如图所示，△即为所求；点，的坐标分别为和；（2）如图所示，△就是与关于原点对称的图形．23．（8分）已知关于的一元二次方程．（1）求证：当时，方程一定有两个不相等的实数根；（2）已知是它的一个实数根，若，求的值．【解答】（1）证明：，，一定大于0，当时，方程一定有两个不相等的实数根； （2）解：是它的一个实数根，．，，整理得：，解得：或，，．24．（10分）如图1所示，将一个边长为2的正方形和一个长为2、宽为1的长方形拼在一起，构成一个大的长方形．现将小长方形绕点顺时针旋转至，旋转角为．（1）当点恰好落在边上时，求旋转角的值；（2）如图2，为中点，且，求证：；（3）小长方形绕点顺时针旋转一周的过程中，与能否全等？若能，直接写出旋转角的值；若不能说明理由．【解答】（1）解：长方形绕点顺时针旋转至，，在中，，，，，； （2）证明：为中点，，，长方形绕点顺时针旋转至，，，，在和△中，△，； （3）解：能．理由如下：四边形为正方形，，，与为腰相等的两等腰三角形，当时，，当与为钝角三角形时，则旋转角，当与为锐角三角形时，则，即旋转角的值为或时，与全等．25．（10分）已知二次函数．（1）求证：当时，任意实数，对应的函数值；（2）该函数图象是否可以通过函数的图象平移得到，如果能，请写出变化过程．【解答】（1）证明：当时，则，函数有最小值1，任意实数，对应的函数值；（2）解：能，由平移的规律可知，二次函数的图象向上平移个单位，即可得到二次函数．26．（10分）如图，是半圆的直径，点是半圆上不同于，的一动点，在弧上取点，使，为半圆的切线，过点作于点．（1）求证：；（2）连接，．探究：当等于多少度时，四边形为菱形，并且写出证明过程．【解答】（1）证明：连接，为半圆的切线，，，，，，，，，，；（2）当时，四边形为菱形，证明：是直径，，，，，，，，，，，，，，四边形是平行四边形，又，四边形是菱形．27．（12分）我市某乡镇在“精准扶贫”活动中销售一农产品，经分析发现月销售量（万件）与月份（月的关系为：，每件产品的利润（元与月份（月的关系如下表：123456789101112191817161514131211101010（1）请你根据表格求出每件产品利润（元与月份（月的关系式；（2）若月利润（万元）当月销售量（万件）当月每件产品的利润（元，求月利润（万元）与月份（月的关系式；（3）当为何值时，月利润有最大值，最大值为多少？【解答】解；（1）当时，设每件产品利润（元与月份（月的关系式为，，得，即当时，每件产品利润（元与月份（月的关系式为，当时，，由上可得，；（2）当时，，当时，，当时，，由上可得，；（3）当时，，当时，取得最大值，此时；当时，，当时，，则当时，取得最大值，此时，由上可得，当为8时，月利润有最大值，最大值144万元．声明：试题解析著作权属菁优网所有，未经书面同意，不得复制发布日期：2021/12/10 18:32:33；用户：初中数学2；邮箱：jse033@xyh.com；学号：39024123