第13讲 旋转中的最值、路径长-讲义（学生版+教师版）2021-2022学年九年级数学人教版上册学案

这是一份第13讲 旋转中的最值、路径长-讲义（学生版+教师版）2021-2022学年九年级数学人教版上册学案，文件包含第13讲旋转中的最值路径长-讲义2021-2022学年九年级数学人教版上册学生版doc、第13讲旋转中的最值路径长-讲义2021-2022学年九年级数学人教版上册教师版doc等2份学案配套教学资源，其中学案共13页， 欢迎下载使用。
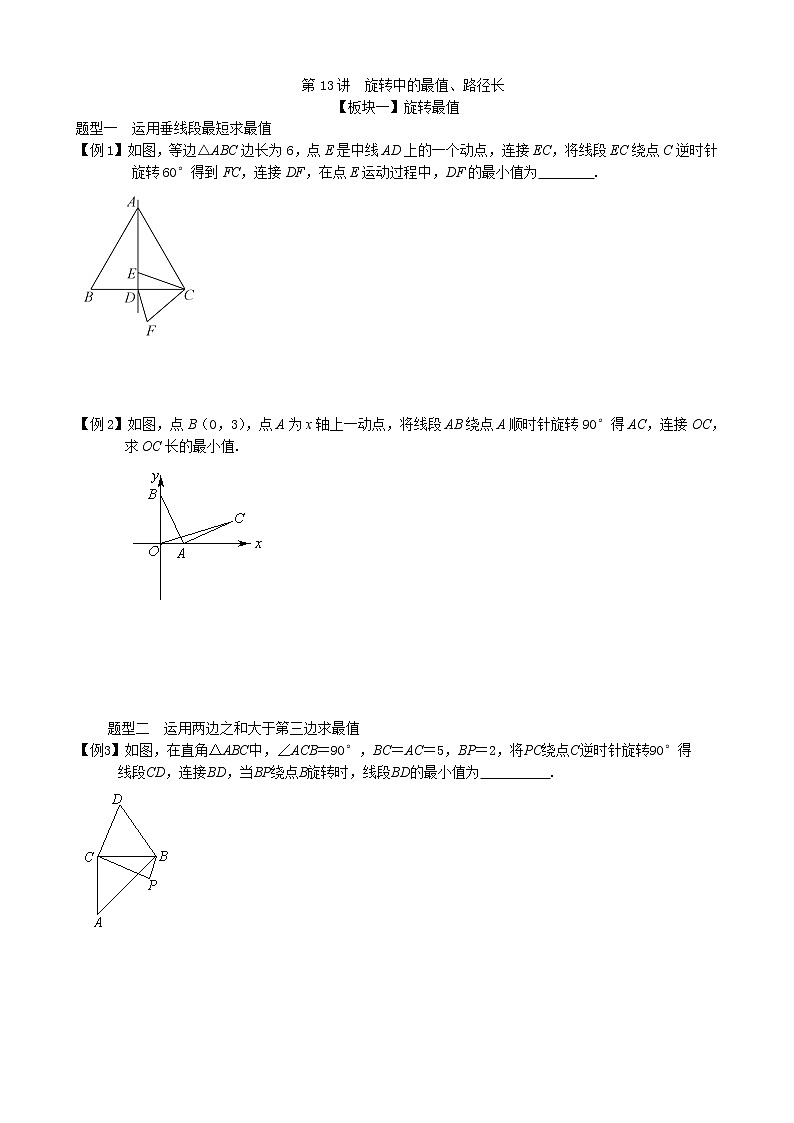
第13讲  旋转中的最值、路径长【板块一】旋转最值题型一  运用垂线段最短求最值【例1】如图，等边△ABC边长为6，点E是中线AD上的一个动点，连接EC，将线段EC绕点C逆时针旋转60°得到FC，连接DF，在点E运动过程中，DF的最小值为        .【解析】取AC的中点G，连接EG，在△DCF和△GCE中，CE＝CF，∠DCF＝∠GCE，∴△DCF≌△GCE（SAS），∴DF＝EG.根据垂线段最短，EG⊥AD时，EG最短，即DF最短，∵，，∴EG的最小值为，∴DF的最小值为1.5.【例2】如图，点B（0，3），点A为x轴上一动点，将线段AB绕点A顺时针旋转90°得AC，连接OC，求OC长的最小值.【解析】在x轴正半轴上取点F，使OF＝OB＝3，延长CF交y轴于点D，在OB上截取OE＝OA.证△AFC≌△BEA. ∴∠CFA＝∠AEB＝135°，得点C在直线DF上运动，△ODF为等腰直角三角形，当OC⊥DF时OC最小为. 题型二  运用两边之和大于第三边求最值【例3】如图，在直角△ABC中，∠ACB＝90°，BC＝AC＝5，BP＝2，将PC绕点C逆时针旋转90°得线段CD，连接BD，当BP绕点B旋转时，线段BD的最小值为          .【解析】连接AP，∴△DCB≌△PCA（SAS），∴AP＝BD，当点P在AB的延长线上时，AP的最大值＝AB＋PB＝＋2，∴BD的最大值为.【例4】如图，△ABC为等腰直角三角形，∠ACB＝90°，BC＝CA.若AC＝，点P为BC的中点，动点Q满足PQ＝，将线段AQ绕点A逆时针旋转90°到线段AM，连PM，则线段PM的最小值为         .【解析】连接AP，将AP绕点A逆时旋转90°到AN，连接PN，MN.易证△APQ≌△ANM，∴MN＝PQ＝，AP＝AN＝，∴PN＝AP＝，，∴PM最小值为.题型三  运用中线，中位线求最值【例5】如图，边长为2的正方形ABCD的对角线交于点O，把边BA，CD分别绕点B，C以相同的速度同时逆时针旋转一周，四边形ABCD的形状也随之发生改变，A'C与D'B交于点O′，那么在旋转的过程中，求AO'的最大值.【解析】首先证A'B∥CD'，得四边形A'BCD'为菱形，∴A'C⊥BD'.取BC的中点G，连接AG，O′G，则O′G＝＝1，AG＝，在△AO′G中，，故AO′的最大值为.  题型四  运用平移、轴对称结合旋转求最值【例6】如图，在等腰△ABC中，∠BAC＝120°，AB＝AC＝，点D在边BC上，CD＝，将线段CD绕点C逆时针旋转（其中0＜≤360）得到CE，连接AE，以AB，AE为边作□ABFE，连接DF，则DF的最大值为（   ）A. B. C. D.【解析】过点C作CO∥AB，CO＝AB，连接OF，则四边形COFE为平行四边形，CO＝EF＝AB＝，OF＝CE＝CD＝，连接DO，则DF≤OD＋OF，由OC//AB，得∠BCO＝∠ABC＝30°，过点O作OH⊥BC于点H，则OH＝，，又DC＝，故HD＝，，因DF≤OD＋OF，而OD＋OF＝，故，∴DF的最大值为.针对练习11.如图，在△ABC中，∠C＝90°，BC＝6，AC＝10，D为线段AC上一动点，将线段BD绕点D逆时针旋转90°.点B的对应点为点E，连接AE，求AE长的最小值.解：在AC上取点F,使CF＝BC＝6.在CB上取点G，使CG＝CD，可证△DEF≌△BDG，∴∠EFD＝∠BGD＝135°，∴∠AFE＝45°，得点E在直线FE上运动，且AE⊥FE时，AE的最小值为.2.如图，在平面直角坐标系中，点A的坐标为(2，0)，点B的坐标为(5，0)，点P为线段AB外一动点，且PA＝2，将PB绕点P逆时针旋转90°得PM，求AM长的最大值.解：将△APM绕点P顺时针旋转90°得△NPB，连接AN，则BN＝AM，△ANP为等腰直角三角形，∴，又.∴在△ANB中，，即AM长的最大值为. 3.如图，边长为4的正方形ABCD外有点E ，∠AEB＝90°，F为DE的中点，连接CF.求CF的最大值.解：取AB的中点G，过点G作GN⊥CD于点N，延长DC至点M，使CM＝CD，则MN＝6，GN＝4，∴GM＝＝2，又EG＝AB＝2，∴在△EMG中，EG≤2＋2，而FC＝EM，故FC≤＋1，∴CF的最大值是＋1.【板块二】旋转图形中动点的路径与动线段的取值范围题型一  旋转图形中点的运动路径【例1】在平面直角坐标系中，点C沿某条路径运动，以点C为旋转中心，将点A(0，4)逆时针旋转90°到点B(m，1)，若－5≤m≤5，求点C运动的路径长.【解析】如图，过点C作MN∥y轴，AN⊥MN于点N，BM⊥MN于点M，则△CAN≌△BCM，AN＝CM，CN＝BM，∵AN＝xc，CM＝yC－1，CN＝4－ yC，BM＝xC－m，解得xC＝，yC＝，∵－5≤m≤5，∴－2≤m＋3≤8，∴－1≤xC≤4，yC＝xC＋1，当xC＝－1时，C(－1，0)；当xC＝4时，C(4，5)；点C的运动路径为＝5.【例2】如图，在平面直角坐标系中，直线y＝x－1分别交x轴，y轴于点B，点A，点M为直线AB上一动点，连接OM，将线段OM绕点M逆时针旋转90°，点O的对应点为点N.当点M运动时，判断点N的运动路线是什么图形，并说明理由.【解析】点N在直线y＝－x－上运动，理由如下：设M(m，m－1)，过点M作MC⊥OB于点C，过点N作ND⊥MC于点D，可证△OCM≌△MDN，OC＝MD＝m，ND＝CM＝1－m，D(m，－1－m)，N(－1，－1－m），xN＝－1①，yN＝－1－m②，由①＋②×2得：－2－m＋m－1＝xN＋2yN，∴xN＋2yN ＝－3，yN ＝ －x－·题型二  旋转图形中变量的取值范围【例3】在Rt△ABC中，∠ACB＝90°，AC＝BC，D，E分别在AC，BC上，DE∥AB，CF⊥DE于点F，AC＝6，CF＝4，G是AE中点.（1）如图1，直接写出FG，BE的数量关系和位置关系为            ；（2）如图2，将△CFE绕点C旋转，在旋转过程中，线段GF的取值范围是        .【解析】（1）FG＝BE，且FG⊥BE；（2）延长EF至点D，使DF＝EF，连接AD，易得FG＝AD，在Rt△CDE中，CD＝4.由旋转得，当点D在边AC上时，AD最小，最小值为AC－CD＝6－4，FG最小＝AD＝3－2，当点D在边AC延长线时，AD最大，AD最大值为AC＋CD＝6＋4，∴FG最大＝AD＝3＋2，∴3－2≤FG≤3＋2.针对练习21.如图，矩形ABCD中，BC＝2AB＝8.点M，N分别为AD，BC的中点，连接MN，点P是BC边上的动点，将PM绕点P顺时针方向旋转90°得PE，当点P从点B运动到点C的过程中，点E运动的路径长为        .解：过点E作EF⊥BC于点F，是长MN，CE交于点G，证△PMN≌△EPF，∴PF MN＝NC，可证 EF＝FC.∴∠BCE＝45°，即点E在∠BCD外角平分线上运动，运动径为GC＋CQ＝8.2.如图，一副含30°角和45°角的三角板ABC和DEF叠E在一起，边BC与EF重合，BC＝EF＝12cm，点G为边BC(EF)的中点，边FD与AB相交于点H，将△DEF绕点G按顺时针方向旋转，旋转角度从0°到60°的变化过程中，点H相应移动的路径长共为        .解：如图，当旋转角从0°到30°时，H运动路径为HH1，当旋转角从30°到60°时，H运动路径为H1H2，所以H移动的路径长为HH1＋ H1H2＝2HH1＋HH2＝2(9－15)＋[6－(12－12)]＝12－18.3.如图，在Rt△ABO中，∠BOA＝90°，AO＝6，BO＝8，动点P从点A开始沿边AO向点O以每秒1个单位长度的速度运动，动点Q从点O开始沿边OB向点B以每秒2个单位长度的速度运动，连接PQ.点P，Q分别从点A，O同时出发，当其中一点到达端点时，另一点也随之停止运动，在整个运动过程中，求出线段PQ的中点M所经过的路径长.解：以O为原点OA为x轴建立如图所示的直角坐标系，设运动时间为t.则PA＝t，OP＝6－t，OQ＝2t，线段PQ的中点M(，t)，由0≤2t≤8，0≤t≤6，得0≤t≤4.又xM＝，yM＝t，故yw＝－2xM＋6，t＝4时，M(1，4)，t＝0时，M(3，0)，故点M所经过的路径为＝2.