专题12.17 三角形全等作辅助线模型（三）-倍长中线（专项练习）（巩固篇）-2021-2022学年八年级数学上册基础知识专项讲练（人教版）

这是一份专题12.17 三角形全等作辅助线模型（三）-倍长中线（专项练习）（巩固篇）-2021-2022学年八年级数学上册基础知识专项讲练（人教版），共34页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。

专题12.17 三角形全等作辅助线模型（三）-倍长中线
（专项练习）（巩固篇）
一、单选题
1．如图，AD是的中线，E是AD上一点，连接BE并延长交AC于点F，若EF=AF， BE=7.5， CF=6，则EF=( ).

A．2.5 B．2 C．1.5 D．1
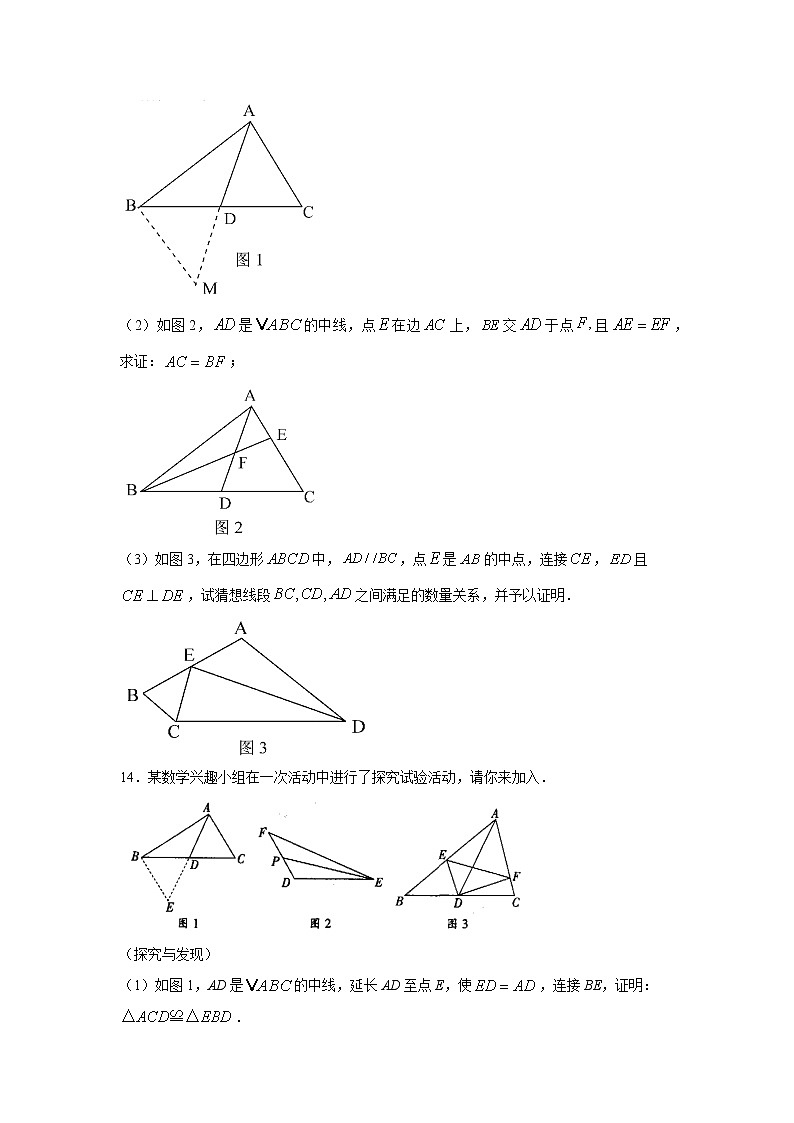
2．在△ABC中，AC＝5，中线AD＝4，那么边AB的取值范围为(　　)
A．1＜AB＜9 B．3＜AB＜13 C．5＜AB＜13 D．9＜AB＜13
3．如图，在△ABC中，AC=5，中线AD=7，则AB边的取值范围是( )

A． B．
C． D．
4．已知△ABC中，AB=5，AC=7，则BC边上的中线a的取值范围是（　　）
A．1＜a＜6 B．5＜a＜7 C．2＜a＜12 D．10＜a＜14
5．AD 是DABC 中 BC 边上的中线，若 AB = 3 ， AD = 4 ，则 AC 的取值范围是（ ）
A．1 < AC < 7 B．0.5 < AC < 3.5 C．5 < AC < 11 D．2.5 < AC < 5.5


二、填空题
6．在△ABC中，AC=8，中线AD=5，那么边AB的取值范围为____．
7．已知在△ABC中，AB＝9，中线AD＝4，那么AC的取值范围是____
8．在中，是边上的中线，若，则长的取值范围是_________．
9．如图，中，为的中点，是上一点，连接并延长交于，，且，，那么的长度为__．

10．如图，△ABC中，BC边上的中线AD将∠BAC分成了两角∠BAD、∠DAC分别为70°和40°，若中线AD长为2.4cm，则AC长为________cm.

11．如图，在△ABC中，∠BAC＝120°，点D是BC的中点，且AD⊥AC，若AC＝3，则AB的长为________．

12．AD是△ABC的边BC上的中线，AB＝12，AC＝8，则边BC的取值范围是_______________________；中线AD的取值范围是__________________．

三、解答题
13．在通过构造全等三角形解决的问题中，有一种典型的方法是倍延中线．
（1）如图1，是的中线，求的取值范围．我们可以延长到点，使，连接，易证，所以．接下来，在中利用三角形的三边关系可求得的取值范围，从而得到中线的取值范围是 ；

（2）如图2，是的中线，点在边上，交于点且，求证：；

（3）如图3，在四边形中，，点是的中点，连接，且，试猜想线段之间满足的数量关系，并予以证明．

14．某数学兴趣小组在一次活动中进行了探究试验活动，请你来加入．

（探究与发现）
（1）如图1，AD是的中线，延长AD至点E，使，连接BE，证明：．
（理解与应用）
（2）如图2，EP是的中线，若，，设，则x的取值范围是________．
（3）如图3，AD是的中线，E、F分别在AB、AC上，且，求证：．
15．如图，已知AD是的中线，过点B作BE⊥AD，垂足为E．若BE=6，求点C到AD的距离．

16．（1）如图1，在ABC中，AB=4，AC=6，AD是BC边上的中线，延长AD到点E使DE=AD，连接CE，把AB，AC，2AD集中在ACE中，利用三角形三边关系可得AD的取值范围是　 　；
（2）如图2，在ABC中，AD是BC边上的中线，点E，F分别在AB，AC上，且DE⊥DF，求证：BE+CF＞EF；
（3）如图3，在四边形ABCD中，∠A为钝角，∠C为锐角，∠B+∠ADC=180°，DA=DC，点E，F分别在BC，AB上，且∠EDF=∠ADC，连接EF，试探索线段AF，EF，CE之间的数量关系，并加以证明．

17．阅读下面文字并填空：数学课上张老师出了这样一道题：“如图，在中，，是中线，点为的中点，连接.求证：”

张老师给出了如下简要分析：“要证，就是要证线段的倍分问题，所以有两个思路，思路一：找，故取的中点，连接，只要证即可.这就将证明线段倍分问题______为证明线段相等问题，只要证出______，则结论成立.思路二：变为，因为需要找到，于是延长至点，使，只要证______即可.连接，若证出____________则结论成立.”你认为在现阶段可以用思路______来完成这个证明.
18．如图，在△ABC中，已知：点D是BC中点，连接AD并延长到点E，连接BE.

（1）请你添加一个条件使△ACD≌△EBD，并给出证明.
（2）若，，求边上的中线的取值范围.
19．（1）阅读理解：课外兴趣小组活动时，老师提出了如下问题：
在△ABC中，AB＝9，AC＝5，求BC边上的中线AD的取值范围．
小明在组内经过合作交流，得到了如下的解决方法（如图1）：
①延长AD到Q，使得DQ＝AD；
②再连接BQ，把AB、AC、2AD集中在△ABQ中；
③利用三角形的三边关系可得4 感悟：解题时，条件中若出现“中点”“中线”等条件，可以考虑倍长中线，构造全等三角形，把分散的己知条件和所求证的结论集中到同一个三角形中．
（2）请你写出图1中AC与BQ的位置关系并证明．
（3）思考：已知，如图2，AD是△ABC的中线，AB＝AE，AC＝AF，∠BAE＝∠FAC＝90°．试探究线段AD与EF的数量和位置关系并加以证明．

20．（1）（问题情境）
课外兴趣小组活动时，老师提出了如下问题：
如图①，在△ABC中，AD是△ABC的中线，若AB＝10，AC＝8，求AD的取值范围．

小明在组内经过合作交流，得到了如下的解决方法：延长AD至点E，使DE＝AD，连接BE．请根据小明的方法思考：
Ⅰ.由已知和作图能得到△ADC≌△EDB，依据是________．
A．SSS B．SAS C．AAS D．ASA
Ⅱ.由“三角形的三边关系”可求得AD的取值范围是________．
解后反思：题目中出现“中点”、“中线”等条件，可考虑延长中线构造全等三角形，把分散的已知条件和所求证的结论集中到同一个三角形之中．
（2）（学会运用）
如图②，AD是 △ABC的中线，点E在BC的延长线上，CE=AB, ∠BAC=∠BCA, 求证：AE=2AD．
21．“综合与实践”学习活动准备制作一组三角形，记这些三角形分别为，用记号表示一个满足条件的三角形，如（2，4，4）表示边长分别为2，4，4个单位长度的一个三角形.
（1）若这些三角形三边的长度为大于0且小于3的整数个单位长度，请用记号写出所有满足条件的三角形；
（2）如图，是的中线，线段的长度分别为2个，6个单位长度，且线段的长度为整数个单位长度，过点作交的延长线于点.

①求的长度；
②请直接用记号表示.
22．如图，已知是的一条中线，延长至，使得，连接. 如果，试求的取值范围.

23．已知：如图，AD，AE分别是△ABC和△ABD的中线，且BA＝BD．求证：AE＝AC．

24．如图，CE、CB分别是△ABC与△ADC的中线，且∠ACB=∠ABC．求证：CD=2CE．

25．先阅读，再回答问题：如图1，已知△ABC中，AD为中线．延长AD至E，使DE=AD．在△ABD和△ECD中，AD=DE，∠ADB=∠EDC，BD=CD，所以，△ABD≌△ECD（SAS），进一步可得到AB=CE，AB∥CE等结论．
在已知三角形的中线时，我们经常用“倍长中线”的辅助线来构造全等三角形，并进一步解决一些相关的计算或证明题．
解决问题：如图2，在△ABC中，AD是三角形的中线，F为AD上一点，且BF=AC，连结并延长BF交AC于点E，求证：AE=EF．


参考答案
1．C
【分析】延长AD，使DG=AD，连接BG，由“SAS”可证△ADC≌△GDB，可得AC=DG=CF+AF=6+AF，∠DAC=∠G，由等腰三角形的性质可得BE=BG=7.5，即可求EF的长．
【详解】
解：如图，延长AD，使DG=AD，连接BG，

∵AD是△ABC的中线，
∴BD=CD，且DG=AD，∠ADC=∠BDG，
∴△ADC≌△GDB（SAS），
∴AC=DG=CF+AF=6+AF，∠DAC=∠G，
∵EF=AF，
∴∠DAC=∠AEF，
∴∠G=∠AEF=∠BEG，
∴BE=BG=7.5，
∴6+AF=BG=7.5，
∴AF=1.5=EF，
故选择：C．
【点拨】本题考查了全等三角形的判定和性质，等腰三角形的性质，添加恰当辅助线构造全等三角形是本题的关键．
2．B
【解析】
试题解析：延长AD至E，使DE=AD=4，连接BE．则AE=8，

∵AD是边BC上的中线，D是中点，
∴BD=CD；
又∵DE=AD，∠BDE=∠ADC，∴△BDE≌△ADC，
∴BE=AC=5；
由三角形三边关系，得AE-BE＜AB＜AE+BE，
即8-5＜AB＜8+5，
∴3＜AB＜13；
故选B．
考点：1．全等三角形的判定与性质；2．三角形三边关系．
3．D
【解析】
延长AD到E，使DE=AD，连接BE

在△ADC和△EDB中
AD=DE,∠ADC=∠BDE,CD=BD
∴△ADC≌△EDB（SAS）
∴AC=BE（全等三角形的对应边相等）
∵AC=5，AD=7
∴BE=5，AE=14
在△ABE中，AE-BE＜AB＜AE+BE
∴AB边的取值范围是：9＜AB＜19
故选D
4．A
【详解】
试题分析：延长AE到D，使AE=DE，连接BD．

∵AE是中线，
∴BE=CE，∠AEC=∠DEB，
∴△AEC≌△DEB△（SAS），
∴BD=AC=7，又AE=a，
∴2＜2a＜12，
∴1＜a＜6．
故选A．
考点：1.全等三角形的判定与性质；2.三角形三边关系．
5．C
【解析】
【分析】延长AD到E，使DE=AD，然后利用“边角边”证明△ABD和△ECD全等，根据全等三角形对应边相等可得CE=AB，然后根据三角形任意两边之和大于第三边，两边之差小于第三边求出AC的取值范围即可．
【详解】
如图，延长AD到E，使DE=AD=4，
∵AD是BC边上的中线，
∴BD=CD,
在△ABD和△ECD中，
∵
∴△ABD≌△ECD(SAS)，
∴CE=AB=3，
∵AB=3，AD=4，
∴AE−CE ∴5 故选C.
【点拨】考查全等三角形的判定与性质，三角形三边关系，熟练作出辅助线是解题的关键.
6．2＜AB＜18
【分析】作出图形，延长AD至E，使DE=AD，然后利用“边角边”证明△ABD和△ECD全等，根据全等三角形对应边相等可得AB=CE，再利用三角形的任意两边之和大于第三边，三角形的任意两边之差小于第三边求出CE的取值范围，即为AB的取值范围．
【详解】
解：如图，延长AD至E，使DE=AD，

∵AD是△ABC的中线，
∴BD=CD，
在△ABD和△ECD中，
，
∴△ABD≌△ECD（SAS），
∴AB=CE，
∵AD=5，
∴AE=5+5=10，
∵10+8=18，10-8=2，
∴2＜CE＜18，
即2＜AB＜18．
故答案为：2＜AB＜18．
【点拨】本题考查了全等三角形的判定与性质，三角形的任意两边之和大于第三边，三角形的任意两边之差小于第三边，“遇中线，加倍延”构造出全等三角形是解题的关键．
7．1＜AC＜17
【分析】作出图形，延长AD至E，使DE＝AD，然后利用“边角边”证明△ABD和△ECD全等，根据全等三角形对应边相等可得AB＝CE，再利用三角形的任意两边之和大于第三边，三角形的任意两边之差小于第三边求出AC的取值范围．
【详解】
如图，延长AD至E，使DE＝AD，

∵AD是△ABC的中线，
∴BD＝CD，
在△ABD和△ECD中，
，
∴△ABD≌△ECD(SAS)，
∴AB＝CE，
∵AD＝4，
∴AE＝4+4＝8，
∵AC+CE＞AC＞CE-AE，
∴9-8＜AC＜8+9，
∴1＜AC＜17，
故答案为：1＜AC＜17．
【点拨】本题考查了全等三角形的判定与性质，三角形的任意两边之和大于第三边，三角形的任意两边之差小于第三边，“遇中线，加倍延”构造出全等三角形是解题的关键．
8．
【分析】利用中线的性质，作辅助线AD=DE，构造全等三角形，再有全等三角形对应边相等的性质，解得，最后由三角形三边关系解题即可．
【详解】
如图，AD为BC边上的中线,延长AD至点E，使得AD=DE

在△ADB和△EDC中






故答案为：．
【点拨】本题考查三角形三边的关系，其中涉及全等三角形的判定与性质等知识，是重要考点，掌握相关知识、正确作出辅助线是解题的关键．
9．；
【分析】延长至使，连接，得出,得出，所以得出是等腰三角形，根据已知线段长度建立等量关系计算．
【详解】

如图：延长至使，连接
在和中：

∴
∴
∵
∴
∴
∵
∴
∴
∴
即
∴
【点拨】倍长中线是常见的辅助线、全等中相关的角的代换是解决本题的关键．
10．4.8
【分析】延长AD到E，取DE=AE，连接CE，用边角边可证△ABD≌△ECD，可得∠E=∠BAD=70°，由∠DAC=40°，可推出△ACE为等腰三角形，则AC=AE.
【详解】
延长AD到E，取DE=AE，连接CE，如图所示，

在△ABD和△ECD中，

∴
∴∠E=∠BAD=70°
在△AEC中，
∴∠E=∠ACE，
∴AC=AE=2AD=4.8cm
故答案为4.8
【点拨】本题考查全等三角形的判定与性质，利用“倍长中线法”构造全等三角形是解题的关键.
11．6
【解析】
【分析】延长AD至E，使DE=AD，连接BE，由∠BAC=120°，∠DAC=90°，可得∠BAE =30°，根据SAS可证明△BED≌△CAD，从而可得∠BED=∠DAC=90°，BE=AC，再根据30度角所对的直角边等于斜边的一半即可求得AB的长.
【详解】延长AD至E，使DE=AD，连接BE，
∵∠BAC=120°，∠DAC=90°，
∴∠BAE=∠BAC-∠DAC=30°，
在△BED和△CAD中，
，
∴△BED≌△CAD（SAS），
∴∠BED=∠DAC=90°，BE=AC=3，
∴AB=2BE=6，
故答案为6.

【点睛】本题考查了全等三角形的判定与性质、含30度角的直角三角形的性质，正确添加辅助线构造出含30度角的直角三角形是解题的关键.
12．4＜BC＜20 2＜AD＜10
【详解】
试题分析：BC边的取值范围可在△ABC中利用三角形的三边关系进行求解，而对于中线AD的取值范围可延长AD至点E，使AD=DE，得出△ACD≌△EBD，进而在△ABE中利用三角形三边关系求解．
解：如图所示，
在△ABC中，则AB﹣AC＜BC＜AB+AC，
即12﹣8＜BC＜12+8，4＜BC＜20，
延长AD至点E，使AD=DE，连接BE，
∵AD是△ABC的边BC上的中线，∴BD=CD，
又∠ADC=∠BDE，AD=DE
∴△ACD≌△EBD，∴BE=AC，
在△ABE中，AB﹣BE＜AE＜AB+BE，即AB﹣AC＜AE＜AB+AC，
12﹣8＜AE＜12+8，即4＜AE＜20，
∴2＜AD＜10．
故此题的答案为4＜BC＜20，2＜AD＜10．

考点：全等三角形的判定与性质；三角形三边关系．
13．（1）；（2）见解析；（3），证明见解析
【分析】（1）延长到点，使，连接，即可证明，则可得，在中，根据三角形三边关系即可得到的取值范围，进而得到中线的取值范围；
（2）延长到点使，连接，由（1）知，则可得，由可知，，由角度关系即可推出，故，即可得到；
（3）延长到，使，连接，即可证明，则可得由，以及角度关系即可证明点在一条直线上，通过证明≌，即可得到，进而通过线段的和差关系得到．
【详解】
（1）延长到点，使，连接，
∵是的中线，
∴，
在和中，
，，，
∴，
∴，
在中，
，
∴，即，
∴；
（2）证明:延长到点使,连接，
由（1）知，

∴，
，
，
，
，
，
，
，
（3），
延长到，使，连接，


，
，
，
，
，
点在一条直线上，
，
∴，
∴在和中，
，，，
∴≌，
，
∵，
．
【点拨】本题考查了三角形中线、全等三角形的证明和性质、三角形的三边关系、等腰三角形的性质、平行线的性质、平角的概念、线段的和差关系等，正确的作出辅助线以及综合运用以上知识是解答本题的关键．
14．（1）见解析；（2）；（3）见解析
【分析】（1）根据全等三角形的判定即可得到结论；
（2）延长至点，使，连接，根据全等三角形的性质得到，根据三角形的三边关系即可得到结论；
（3）延长FD至G，使得，连接BG，EG，结合前面的做题思路，利用三角形三边关系判断即可．
【详解】
（1）证明：，，，
，
（2）；
如图，延长至点，使，连接，

在与中，
，
，
，
在中，，
即，
的取值范围是；
故答案为：；
（3）延长FD至G，使得，连接BG，EG，
在和中，，，，
，，
在和中，
，，，
，，
在中，两边之和大于第三边
，，
又，，


【点拨】本题考查了全等三角形的判定和性质，三角形的中线的定义，三角形的三边关系，正确的作出图形是解题的关键．
15．6
【分析】延长AD，过点C作于点F，证明，再根据全等三角形的性质得到．
【详解】
解：如图，延长AD，过点C作于点F，
∵AD是的中线，
∴，
∵，，
∴，
在和中，
，
∴，
∴，即点C到AD的距离是6．

【点拨】本题考查全等三角形的性质和判定，解题的关键是利用倍长中线的方法做辅助线构造全等三角形，利用全等三角形的性质求解．
16．（1）1＜AD＜5；（2）见解析；（3）AF+EC=EF，见解析
【分析】（1）证明△CDE≌△BDA（SAS），推出CE=AB=4，在△ACE中，利用三角形的三边关系解决问题即可．
（2）如图2中，延长ED到H，使得DH=DE，连接DH，FH．证明△BDE≌△CDH（SAS），推出BE=CH，再证明EF=FH，利用三角形的三边关系即可解决问题．
（3）结论：AF+EC=EF．延长BC到H，使得CH=AF．提供两次全等证明AF=CE，EF=EH即可解决问题．
【详解】
（1）∵CD=BD，AD=DE，∠CDE=∠ADB，
∴△CDE≌△BDA（SAS），
∴EC=AB=4，
∵6﹣4＜AE＜6+4，
∴2＜2AD＜10，
∴1＜AD＜5，
故答案为：1＜AD＜5；
（2）如图2中，延长ED到H，使得DH=DE，连接DH，FH．

∵BD=DC，∠BDE=∠CDH，DE=DH，
∴△BDE≌△CDH（SAS），
∴BE=CH，
∵FD⊥EH，又DE=DH，
∴EF=FH，
在△CFH中，CH+CF＞FH，
∵CH=BE，FH=EF，
∴BE+CF＞EF；
（3）结论：AF+EC=EF．
理由：延长BC到H，使得CH=AF．

∵∠B+∠ADC=180°，
∴∠A+∠BCD=180°，
∵∠DCH+∠BCD=180°，
∴A=∠DCH，
∵AF=CH，AD=CD，
∴△AFD≌△CHD（SAS），
∴DF=DH，∠ADF=∠CDH，
∴∠ADC=∠FDH，
∵∠EDF=∠ADC，
∴∠EDF=∠FDH，
∴∠EDF=∠EDH，
∵DE=DE，
∴△EDF≌△EDH（SAS），
∴EF=EH，
∵EH=EC+CH=EC+AF，
∴EF=AF+EC．
【点拨】本题考查了全等三角形的判定和性质，三角形的中线的性质，三角形的三边关系等知识，解题的关键是学会倍长中线，构造全等三角形解决问题，属于中考常考题型．
17．转化；；, , ；二
证明过程见详解
【分析】按照张老师的思路即可填出答案，利用全等三角形的判定及性质来证明，从而有，从而结论可证.所以思路二可以证明.
【详解】
转化；；, , ；二
证明：延长至点，使
∵点为的中点
∴
在和中，


∵，是中线




在和中，

∴
∴
【点拨】本题主要考查全等三角形的判定及性质，掌握全等三角形的判定方法是解题的关键.
18．添加AD=DE，证明见解析；（2）1 【分析】（1）根据全等三角形的判定定理添加AD=DE，利用SAS即可证明△ACD≌△EBD；（2）延长AD到E，使AD=ED，由（1）可得△ACD≌△EBD，可得BE=AC=3，在△ABE中，根据三角形三边关系可得AE的取值范围，进而可得答案.
【详解】
（1）可添加AD=DE，理由如下：
∵点D是BC中点，
∴BD=DC，
在△ADC和△EDB中，，
∴△ADC≌△EDB（SAS），
（2）延长AD到E，使AD=ED，
由（1）得△ADC≌△EDB，
∴BE=AC，
在△ABE中，AB-BE ∴1 【点拨】本题考查了全等三角形的判定定理的应用及三角形三边关系，全等三角形的判定定理有SAS，ASA，AAS，SSS，HL，熟练掌握全等三角形的判定定理是解题关键.
19．（1）2＜AD＜7；（2）AC∥BQ，理由见解析；（3）EF＝2AD，AD⊥EF，理由见解析
【分析】（1）先判断出BD＝CD，进而得出△QDB≌△ADC（SAS），得出BQ＝AC＝5，最后用三角形三边关系即可得出结论；
（2）由（1）知，△QDB≌△ADC（SAS），得出∠BQD＝∠CAD，即可得出结论；
（3）同（1）的方法得出△BDQ≌△CDA（SAS），则∠DBQ＝∠ACD，BQ＝AC，进而判断出∠ABQ＝∠EAF，进而判断出△ABQ≌△EAF，得出AQ＝EF，∠BAQ＝∠AEF，即可得出结论．
【详解】
解：（1）延长AD到Q使得DQ＝AD，连接BQ，
∵AD是△ABC的中线，
∴BD＝CD，
在△QDB和△ADC中， ，
∴△QDB≌△ADC（SAS），
∴BQ＝AC＝5，
在△ABQ中，AB﹣BQ＜AQ＜AB+BQ，
∴4＜AQ＜14，
∴2＜AD＜7，
故答案为2＜AD＜7；
（2）AC∥BQ，理由：由（1）知，△QDB≌△ADC，
∴∠BQD＝∠CAD，
∴AC∥BQ；
（3）EF＝2AD，AD⊥EF，
理由：如图2，延长AD到Q使得BQ＝AD，连接BQ，
由（1）知，△BDQ≌△CDA（SAS），
∴∠DBQ＝∠ACD，BQ＝AC，
∵AC＝AF，
∴BQ＝AF，
在△ABC中，∠BAC+∠ABC+∠ACB＝180°，
∴∠BAC+∠ABC+∠DBQ＝180°，
∴∠BAC+ABQ＝180°，
∵∠BAE＝∠FAC＝90°，
∴∠BAC+∠EAF＝180°，
∴∠ABQ＝∠EAF，
在△ABQ和△EAF中， ，
∴△ABQ≌△EAF，
∴AQ＝EF，∠BAQ＝∠AEF，
延长DA交EF于P，
∵∠BAE＝90°，
∴∠BAQ+∠EAP＝90°，
∴∠AEF+∠EAP＝90°，
∴∠APE＝90°，
∴AD⊥EF，
∵AD＝DQ，
∴AQ＝2AD，
∵AQ＝EF，
∴EF＝2AD，
即：EF＝2AD，AD⊥EF．

【点拨】本题是三角形综合题，主要考查全等三角形的判定和性质，倍长中线法，构造全等三角形是解题的关键．
20．（1）Ⅰ.B；Ⅱ. 1＜AD＜9；（2）证明见解析.
【分析】（1）Ⅰ.根据全等三角形的判定定理解答；
Ⅱ.根据三角形的三边关系定理可得AB−BE＜AE＜AB＋BE，结合BE=AC可确定AE的取值范围，易得AD的取值范围；
（2）首先延长AD至M，使DM＝AD，先证明△ABD≌△MCD，进而得出MC＝AB，∠B＝∠MCD，即可得出∠ACM＝∠ACE，再证明△ACM≌△ACE，即可证明结论．
【详解】
解：（1）Ⅰ.在△ADC和△EDB中，，
∴△ADC≌△EDB（SAS），
故选：B；
Ⅱ.∵△ADC≌△EDB，
∴BE=AC，
∵AB−BE＜AE＜AB＋BE，
∴AB− AC＜AE＜AB＋AC，即2＜AE＜18，
∴1＜AD＜9，
故答案为：1＜AD＜9；
（2）延长AD至M，使DM＝AD，
∵AD是△ABC的中线，
∴BD＝CD，
在△ABD和△MCD中，，
∴△ABD≌△MCD（SAS），
∴MC＝AB，∠B＝∠MCD，
∵AB＝CE，
∴CM＝CE，
∵∠BAC＝∠BCA，
∴∠B＋∠BAC＝∠ACB＋∠MCD，即∠ACE＝∠ACM，
在△ACE和△ACM中，，
∴△ACM≌△ACE（SAS），
∴AE＝AM，
∵AM＝2AD，
∴AE＝2AD．

【点拨】本题考查的是三角形三边关系以及全等三角形的判定和性质，掌握全等三角形的判定定理和性质定理利用倍长中线得出辅助线是解题关键．
21．（1）（1，1，1），（1，2，2），（2，2，2）;（2）①;②（2，6，6）
【解析】
【分析】（1）应用列举法，根据三角形三边关系列举出所有满足条件的三角形．
（2）①根据题意，由AAS可证明，所以，，再根据三角形三边关系可得，即，所以 ，又因为的长度为整数个单位长度，所以得.
②由①得的三边分别是2,6,6,根据题意可得答案.
【详解】
解：（1）因为大于0且小于3的整数的整数有1、2，所以根据三角形三边关系列举出所有满足条件的三角形有：（1，1，1），（1，2，2），（2，2，2）；
（2）①如图 ∵
∴
在和中
∴
∴
∴
在中 ∵
∴
∴
∵的长度为整数个单位长度
∴；
②由①得，的三边分别是2,6,6,根据题意，用记号表示为（2，6，6）.
【点拨】本题考查三角形的三边关系，三角形中线，解题关键是利用中线倍长法做辅助线.
22．的取值范围是.
【解析】
【分析】先证明得到，然后根据三角形的三边关系得到AE的取值范围，从而计算出AD的取值范围。
【详解】
解：∵是中线，
所以（中线的意义）
在和中，

∴
∴ （全等三角形对应边相等）
又在中，
∴，
∴，
∴的取值范围是.
【点拨】本题考查了三角形的中线和三边关系。条件中若出现“中点”“中线”字样，可以考虑把中线延长一倍，把分散的已知条件和所求证的结论集中到同一个三角形中，注意运用类比方法构造相应的全等三角形．
23．证明见解析．
【解析】
试题分析：首先根据题意延长至点，使，连结，根据三角形中线的性质得到，然后利用SAS判定≌（SAS），再根据全等三角形的性质得到 利用外角性质及等式的性质得到，利用SAS得到≌，利用全等三角形的对应边相等得到，由，等量代换即可得证.
试题解析：
证明：延长至点，使，连结，
∵是的中线，


∴≌（SAS），



是的中线，

又，
∴≌（SAS），

即
24．见解析
【解析】
试题分析：
如图，考虑到CE是△ABC的中线，我们延长CE到F，使EF=CE，这样CF=2CE，结合已知条件可证△AEC≌△BEF，并可进一步证得△CFB≌△CDB，得到CF=CD，从而可得结论CD=2CE.
试题解析：
如图，延长CE到点F，使EF=CE，则CF=2CE，

∵CE是△ABC的中线，
∴ AE=BE，
在△ACE和△BFE中，
∴ △ ACE≌ △ BFE（AAS），
∴ AC=BF，∠A=∠ABF，
又∵∠ACB=∠ABC，CB是△ADC的中线，
∴ AC=AB=BD=BF，∠DBC=∠A+∠ACB=∠ABF+∠ABC，即∠DBC=∠FBC，
在△DBC和△FBC中， ，
∴△DBC≌△FBC（SAS），
∴DC=CF=2CE．
点睛：在这类有关三角形中线的问题中，延长中线一倍，构造全等三角形是我们在解题中常用的一种辅助线作法，需认真去体会.
25．证明见试题解析．
【详解】
试题分析：延长AD到G，使DF=DG，连接CG，求出BD=DC，根据SAS推出△BDF≌△CDG，根据全等三角形的性质得出BF=CG，∠BFD=∠G，求出∠AFE=∠G，CG=AC，推出∠G=∠CAF，求出∠AFE=∠CAF即可．
试题解析：延长AD到G，使DF=DG，连接CG，

∵AD是中线，∴BD=DC，
在△BDF和△CDG中，∵BD=DC，∠BDF=∠CDG，DF=DG，∴△BDF≌△CDG，
∴BF=CG，∠BFD=∠G，
∵∠AFE=∠BFD，∴∠AFE=∠G，
∵BF=CG，BF=AC，∴CG=AC，∴∠G=∠CAF，∴∠AFE=∠CAF，∴AE=EF．
考点：全等三角形的判定与性质．