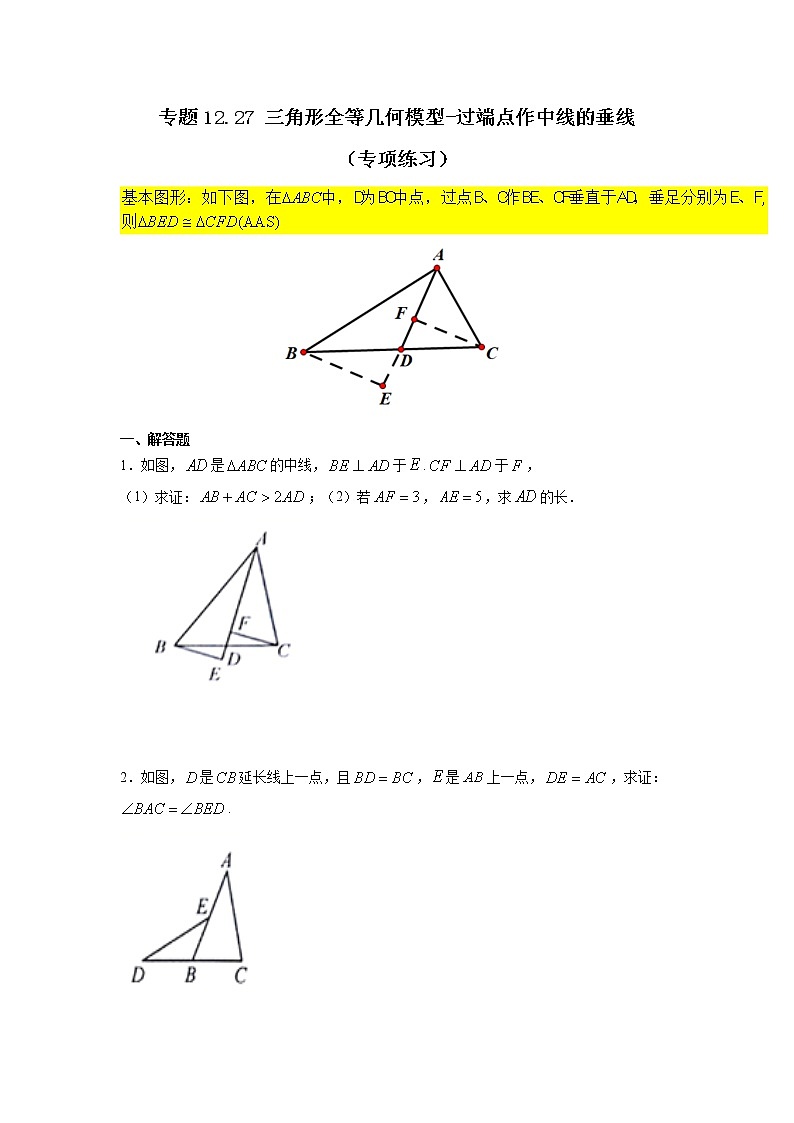
专题12.27 三角形全等几何模型-过端点作中线的垂线（专项练习）-2021-2022学年八年级数学上册基础知识专项讲练（人教版）

这是一份专题12.27 三角形全等几何模型-过端点作中线的垂线（专项练习）-2021-2022学年八年级数学上册基础知识专项讲练（人教版），共9页。试卷主要包含了解答题等内容，欢迎下载使用。
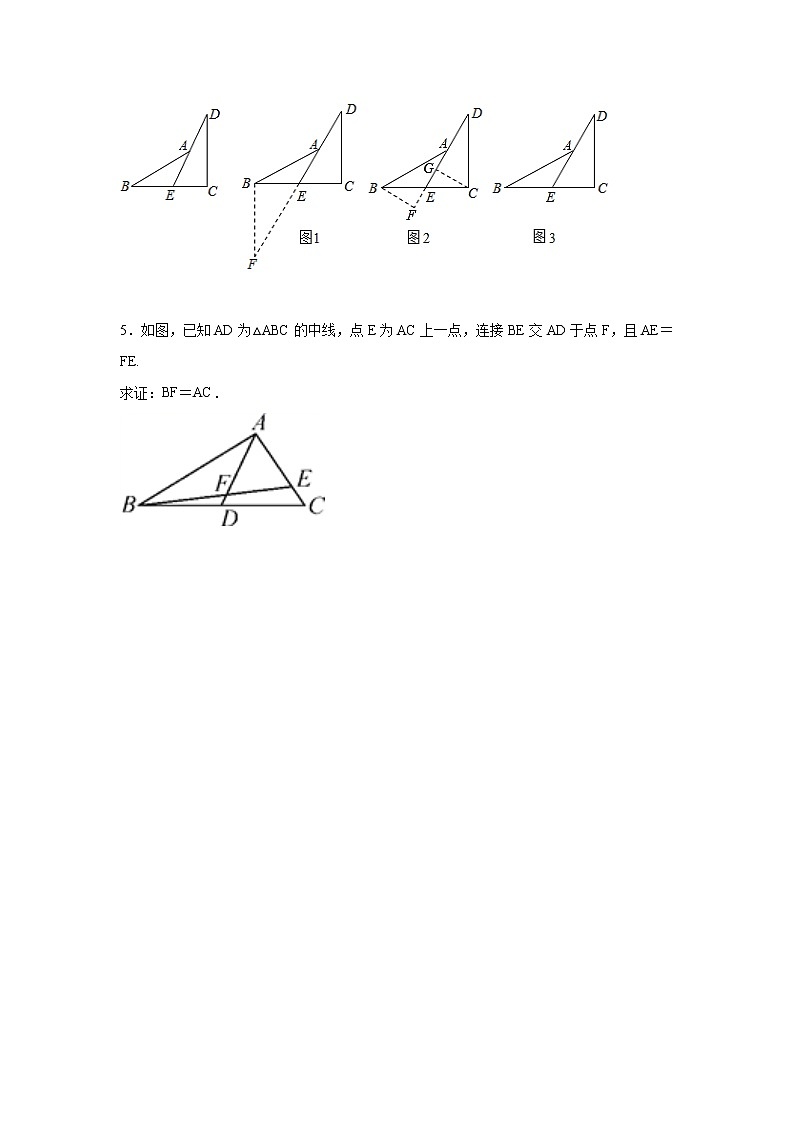
专题12.27 三角形全等几何模型-过端点作中线的垂线（专项练习） 一、解答题1．如图，是的中线，于.于，（1）求证：；（2）若，，求的长．  2．如图，是延长线上一点，且，是上一点，，求证：.   3．如图，在中，，，，，延长交于.求证：.   4．阅读下面的题目及分析过程，并按要求进行证明．已知：如图，点E是BC的中点，点A在DE上，且∠BAE＝∠CDE．求证：AB＝CD．分析：证明两条线段相等，常用的方法是应用全等三角形或等腰三角形的判定和性质，观察本题中要证明的两条线段，它们不在同一个三角形中，且它们分别所在的两个三角形也不全等，因此，要证AB＝CD，必须添加适当的辅助线，构造全等三角形或等腰三角形．（1）现给出如下两种添加辅助线的方法，请任意选出其中一种，对原题进行证明．①如图1，延长DE到点F，使EF＝DE，连接BF；②如图2，分别过点B、C作BF⊥DE，CG⊥DE，垂足分别为点F，G．（2）请你在图3中添加不同于上述的辅助线，并对原题进行证明． 5．如图，已知AD为△ABC的中线，点E为AC上一点，连接BE交AD于点F，且AE＝FE.求证：BF＝AC．
参考答案1．（1）详见解析；（2）【解析】【分析】先证明DE=DF；(1)在中，由垂线段最短可得，即，①，在中，同理可得，即，②，①+②整理后即可得结论；(2)， ，可得，继而可得答案.【详解】∵BE⊥AD，CF⊥AD，∴∠BED=∠CFD=90°，∵AD为△ABC的中线，∴BD=CD，又∠BDE＝CDF∴△BED≌△CFD(AAS)，∴DE=DF；(1)在中，，即，①在中，，即，②①+②得，，即；(2)，①，，②①+②得，，【点拨】本题考查了全等三角形的判定与性质，垂线段最短的性质，正确运用数形结合思想是解题的关键.2．详见解析【解析】【分析】分别过点D、C作AB的垂线，构建与，证其全等即可求得答案.【详解】如图，过点C作于点G，过点D作的延长线于点F，则有∠DFB=∠CGB=∠CGA=90°，又∵∠DBF=∠CBG，BD=BC，∴，∴DF=CG，.又，∴≌，.【点拨】本题考查了全等三角形的判定与性质，正确添加辅助线，熟练掌握三角形全等的判定方法是解题的关键.3．详见解析【解析】【分析】如图，过点D作的延长线于点G，易证，再证即可得答案.【详解】如图，过点D作的延长线于点G，，，，又∵∠ACB=∠BGD=90°，BA=BD，∴，，又∵BC=BE，，又∵∠EBF=∠DGF=90°，∠EFB=∠DFG，∴，∴EF=DF.【点拨】本题考查了全等三角形的判定与性质，学会添加常用辅助线，熟练掌握全等三角形的判定方法是解题的关键.4．（1）①见解析；②见解析；（2）见解析；【分析】（1）①如图1，延长DE到点F，使EF＝DE，连接BF，△BEF≌△CED，∠BAE＝∠F， AB＝CD；②如图2，分别过点B、C作BF⊥DE，CG⊥DE，垂足分别为点F，G，△BEF≌△CEG△BAF≌△CDG，AB＝CD；（2）如图3，过C点作CM∥AB，交DE的延长线于点M，则∠BAE＝∠EMC，△BAE≌△CFE（AAS），∠F＝∠EDC，CF＝CD，AB＝CD；【详解】（1）①如图1，延长DE到点F，使EF＝DE，连接BF，∵点E是BC的中点，∴BE＝CE，在△BEF和△CED中， ，∴△BEF≌△CED（SAS），∴BF＝CD，∠F＝∠CDE，∵∠BAE＝∠CDE，∴∠BAE＝∠F，∴AB＝BF，∴AB＝CD；②如图2，分别过点B、C作BF⊥DE，CG⊥DE，垂足分别为点F，G，∴∠F＝∠CGE＝∠CGD＝90°，∵点E是BC的中点，∴BE＝CE，在△BEF和△CEG中， ，∴△BEF≌△CEG（AAS），∴BF＝CG， 在△BAF和△CDG中，，∴△BAF≌△CDG（AAS），∴AB＝CD；（2）如图3，过C点作CM∥AB，交DE的延长线于点M，则∠BAE＝∠EMC，∵E是BC中点，∴BE＝CE，在△BAE和△CME中，，∴△BAE≌△CFE（AAS），∴CF＝AB，∠BAE＝∠F，∵∠BAE＝∠EDC，∴∠F＝∠EDC，∴CF＝CD，∴AB＝CD．【点拨】本题主要考查了全等三角形的判定和性质，对顶角相等，平行线的性质，构造出全等三角形是解本题的关键．5．证明见解析【分析】方法一：当题中有三角形中线时，常加倍中线构造平行四边形，利用平行四边形和等腰三角形的性质证得结论．方法二：向中线作垂线，证明，得到，再根据AE＝FE，得到角的关系，从而证明，最终得到结论.【详解】方法一：延长AD到G，使DG＝AD，连接BG，CG，∵DG＝AD，BD＝DC，∴四边形ABGC是平行四边形，∴AC//BG，∠CAD＝∠BGD，又∵AE＝FE，∴∠CAD＝∠AFE，∴∠BGD＝∠AFE＝∠BFG，∴BG＝BF，∵BG＝AC，∴BF＝AC 方法二：如图，分别过点、作，，垂足为、，则.，，，.，，，，又，，.【点拨】本题是较为典型的题型，至少可以用到两种方法来解题，此题的特点就是必须有中线这个条件才能构造平行四边形或双垂线.