专题12.29 《全等三角形》中考真题专练（巩固篇）（专项练习）-2021-2022学年八年级数学上册基础知识专项讲练（人教版）

这是一份专题12.29 《全等三角形》中考真题专练（巩固篇）（专项练习）-2021-2022学年八年级数学上册基础知识专项讲练（人教版），共29页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。

专题12.29 《全等三角形》中考真题专练（巩固篇）（专项练习）
一、单选题
1．（2021·重庆·中考真题）如图，在和中， ，添加一个条件，不能证明和全等的是（ ）

A． B．
C． D．
2．（2018·台湾中考真题）如图，五边形ABCDE中有一正三角形ACD，若AB=DE，BC=AE，∠E=115°，则∠BAE的度数为何？（　　）

A．115 B．120 C．125 D．130
3．（2018·辽宁葫芦岛·中考真题）如图，在△ABC中，∠C=90°，点D在AC上，DE∥AB，若∠CDE=165°，则∠B的度数为（　　）

A．15° B．55° C．65° D．75°
4．（2020·湖南永州·中考真题）如图，已知．能直接判断的方法是（ ）

A． B． C． D．
5．（2020·贵州毕节·中考真题）如图，在一个宽度为长的小巷内，一个梯子的长为，梯子的底端位于上的点，将该梯子的顶端放于巷子一侧墙上的点处，点到的距离为，梯子的倾斜角为；将该梯子的顶端放于另一侧墙上的点处，点到的距离为，且此时梯子的倾斜角为，则的长等于（ ）

A． B． C． D．
6．（2019·山东中考真题）要作∠A′O′B′等于已知角∠AOB，应先作一条射线O′B′，再以点O为圆心，以任意长为半径画弧，交OA于点C，交OB于点D．然后(　　)
A．以点O′为圆心，任意长为半径画弧 B．以点O′为圆心，OB长为半径画弧
C．以点O′为圆心，CD长为半径画弧 D．以点O′为圆心，OD长为半径画弧
7．（2019·山东临沂·中考真题）如图，是上一点，交于点，，，若，，则的长是( )

A．0.5 B．1 C．1.5 D．2
8．（2019·山东青岛·中考真题）如图， BD 是△ABC 的角平分线， AE⊥ BD ，垂足为 F ，若∠ABC＝35°，∠ C＝50°，则∠CDE 的度数为（ ）

A．35° B．40° C．45° D．50°
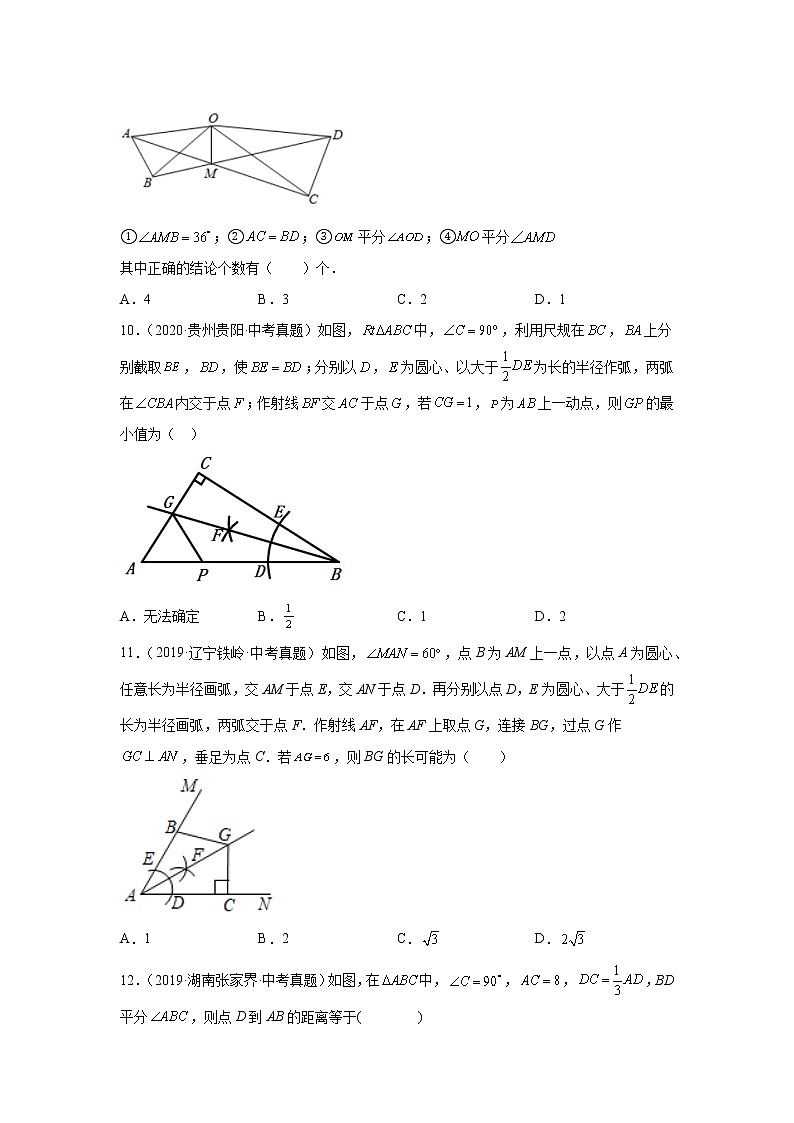
9．（2020·湖北鄂州·中考真题）如图，在和中，，，，．连接、交于点，连接．下列结论：

①；②；③平分；④平分
其中正确的结论个数有（ ）个．
A．4 B．3 C．2 D．1
10．（2020·贵州贵阳·中考真题）如图，中，，利用尺规在，上分别截取，，使；分别以，为圆心、以大于为长的半径作弧，两弧在内交于点；作射线交于点，若，为上一动点，则的最小值为（ ）

A．无法确定 B． C．1 D．2
11．（2019·辽宁铁岭·中考真题）如图，，点B为AM上一点，以点A为圆心、任意长为半径画弧，交AM于点E，交AN于点D．再分别以点D，E为圆心、大于的长为半径画弧，两弧交于点F．作射线AF，在AF上取点G，连接BG，过点G作，垂足为点C．若，则BG的长可能为（　　）

A．1 B．2 C． D．
12．（2019·湖南张家界·中考真题）如图，在中，，，，BD平分，则点D到AB的距离等于( )

A．4 B．3 C．2 D．1
13．（2019·新疆中考真题）如图，在△ABC中，∠C=90°，∠A=30°，以点B为圆心，适当长为半径的画弧，分别交BA，BC于点M、N；再分别以点M、N为圆心，大于MN的长为半径画弧，两弧交于点P，作射线BP交AC于点D，则下列说法中不正确的是（）

A．BP是∠ABC的平分线 B．AD=BD C． D．CD=BD
14．（2019·浙江湖州·中考真题）如图，已知在四边形中，，平分，，，，则四边形的面积是（ ）

A．24 B．30 C．36 D．42
15．（2017·山东滨州·中考真题）如图，在△ABC中，AB＝AC，D为BC上一点，且DA＝DC，BD＝BA，则∠B的大小为(　　)

A．40° B．36° C．30° D．25°


二、填空题
16．（2017·内蒙古包头·中考真题）如图，在△ABC与△ADE中，AB=AC，AD=AE，∠BAC=∠DAE，且点D在AB上，点E与点C在AB的两侧，连接BE，CD，点M、N分别是BE、CD的中点，连接MN，AM，AN．
下列结论：①△ACD≌△ABE；②△ABC∽△AMN；③△AMN是等边三角形；④若点D是AB的中点，则S△ABC=2S△ABE．
其中正确的结论是_____．（填写所有正确结论的序号）

17．（2019·湖北襄阳·中考真题）如图，已知，添加下列条件中的一个：①，②，③，其中不能确定≌△的是_____（只填序号）．

18．（2019·内蒙古呼和浩特·中考真题）下面三个命题：底边和顶角对应相等的两个等腰三角形全等；两边及其中一边上的中线对应相等的两个三角形全等；斜边和斜边上的中线对应相等的两个直角三角形全等，其中正确的命题的序号为_____．
19．（2019·湖南邵阳·中考真题）如图，已知，请你添加一个条件，使得，你添加的条件是_____．（不添加任何字母和辅助线）

20．（2021·黑龙江大庆·中考真题）已知，如图1，若是中的内角平分线，通过证明可得，同理，若是中的外角平分线，通过探究也有类似的性质．请你根据上述信息，求解如下问题：如图2，在中，是的内角平分线，则的边上的中线长的取值范围是________


21．（2020·辽宁铁岭·中考真题）如图，在中，，以为圆心，以适当的长为半径作弧，交于点，交于点，分别以为圆心，以大于的长为半径作弧，两弧在的内部相交于点，作射线，交于点，点在边上，，连接，则的周长为___________．

22．（2020·江苏扬州·中考真题）如图，在中，按以下步骤作图：
①以点B为圆心，任意长为半径作弧，分别交AB、BC于点D、E．
②分别以点D、E为圆心，大于的同样长为半径作弧，两弧交于点F．
③作射线BF交AC于点G．
如果，，的面积为18，则的面积为________．

23．（2017·四川达州·中考真题）△ABC中，AB＝5，AC＝3，AD是△ABC的中线，设AD长为m，则m的取值范围是____．

三、解答题
24．（2021·内蒙古赤峰·中考真题）如图，在Rt△ABC中，∠ACB=90°，且AC=AD．
（1）作∠BAC的平分线，交BC于点E；(要求尺规作图，不写作法，保留作图痕迹)
（2）在（1）的条件下，连接DE，证明．




25．（2020·湖南长沙·中考真题）人教版初中数学教科书八年级上册第48页告诉我们一种作已知角的平分线的方法：
已知：
求作：的平分线
做法：（1）以O为圆心，适当长为半径画弧，交OA于点M，交OB于点N，
（2）分别以点M，N为圆心，大于的长为半径画弧，两弧在的内部相交于点C
（3）画射线OC，射线OC即为所求．

请你根据提供的材料完成下面问题：
（1）这种作已知角平分线的方法的依据是__________________(填序号)．
① ② ③ ④
（2） 请你证明OC为的平分线．



26．（2019·江苏南通·中考真题）如图，有一个池塘，要测池塘两端，的距离，可先在平地上取一个点，从点不经过池塘可以直接达到点和，连接并延长到点，使，连接并延长到点，使，连接，那么量出的长度就是，的距离，为什么？

27．（2019·陕西中考真题）如图，点A，E，F在直线l上，AE=BF，AC//BD，且AC=BD，求证：CF=DE







28．（2019·湖北宜昌·中考真题）如图，在中，是边上的一点，，平分，交边于点，连接．
（1）求证：；
（2）若，，求的度数．








29．（2019·贵州安顺·中考真题）（1）如图①，在四边形中，，点是的中点，若是的平分线，试判断，，之间的等量关系．
解决此问题可以用如下方法：延长交的延长线于点，易证得到，从而把，，转化在一个三角形中即可判断．
，，之间的等量关系________；
（2）问题探究：如图②，在四边形中，，与的延长线交于点，点是的中点，若是的平分线，试探究，，之间的等量关系，并证明你的结论．




































参考答案
1．B
【分析】根据已知条件和添加条件，结合全等三角形的判断方法即可解答．
解：选项A，添加，
在和中，
，
∴≌（ASA），
选项B，添加，
在和中，，，，无法证明≌；
选项C，添加，
在和中，
，
∴≌（SAS）；
选项D，添加，
在和中，
，
∴≌（AAS）；
综上，只有选项B符合题意．
故选B．
【点拨】本题考查了全等三角形的判定方法，熟知全等三角形的判定方法是解决问题的关键．
2．C
解：分析：根据全等三角形的判定和性质得出△ABC与△AED全等，进而得出∠B=∠E，利用多边形的内角和解答即可．
详解：∵三角形ACD为正三角形，
∴AC=AD，∠ACD=∠ADC=∠CAD=60°，
∵AB=DE，BC=AE，
∴△ABC≌△DEA，
∴∠B=∠E=115°，∠ACB=∠EAD，∠BAC=∠ADE，
∴∠ACB+∠BAC=∠BAC+∠DAE=180°﹣115°=65°，
∴∠BAE=∠BAC+∠DAE+∠CAD=65°+60°=125°，
故选C．
点睛：此题考查全等三角形的判定和性质，关键是根据全等三角形的判定和性质得出△ABC与△AED全等．
3．D
【分析】根据邻补角定义可得∠ADE=15°，由平行线的性质可得∠A=∠ADE=15°，再根据三角形内角和定理即可求得∠B=75°．
解：∵∠CDE=165°，∴∠ADE=15°，
∵DE∥AB，∴∠A=∠ADE=15°，
∴∠B=180°﹣∠C﹣∠A=180°﹣90°﹣15°=75°，
故选D．
【点拨】本题考查了平行线的性质、三角形内角和定理等，熟练掌握平行线的性质以及三角形内角和定理是解题的关键．
4．A
【分析】根据三角形全等的判定定理解答.
解：在△ABC和△DCB中，
,
∴(SAS),
故选：A.
【点拨】此题考查全等三角形的判定定理：SSS、SAS、ASA、AAS、HL，根据已知条件找到全等所需的对应相等的边或角是解题的关键.
5．D
【分析】过点C作CE⊥AD于点E，证明≌即可解决问题．
解：过点C作CE⊥AD于点E，则CE//AB，


，且PD=PC，
为等边三角形，
， ，
，
，
， ，
∴ ，
∴ ，
∴ ，
，
在和中，
，
∴≌，
，
故选：D．
【点拨】此题主要考查了全等三角形的应用，作辅助线CE是解答此题的关键．
6．D
【分析】根据作一个角等于已知角的方法判断.
解：要作∠A′O′B′等于已知角∠AOB，
应先作一条射线O′B′，再以点O为圆心，以任意长为半径画弧，交OA于点C，交OB于点D．
然后以点O′为圆心，OD长为半径画弧，再进行画图，
故选D.
【点拨】理解作一个角等于已知角的方法步骤是关键.
7．B
【分析】根据平行线的性质，得出，，根据全等三角形的判定，得出，根据全等三角形的性质，得出，根据，，即可求线段的长．
解：∵，
∴，，
在和中，
∴，
∴，
∵，
∴.
故选B．
【点拨】本题考查了全等三角形的性质和判定，平行线的性质的应用，能判定是解此题的关键．
8．C
【分析】根据角平分线的定义和垂直的定义得到∠ABD=∠EBD=∠ABC=，∠AFB=∠EFB=90°，推出AB=BE，根据等腰三角形的性质得到AF=EF，求得AD=ED，得到∠DAF=∠DEF，根据三角形的外角的性质即可得到结论．
解：∵BD是△ABC的角平分线，AE⊥BD，
∴∠ABD=∠EBD=∠ABC=，∠AFB=∠EFB=90°，
∴∠BAF=∠BEF=90°-17.5°，
∴AB=BE，AE⊥BD
∴BD是AE的垂直平分线，
∴AD=ED，
∴∠DAF=∠DEF，
∵∠BAC=180°-∠ABC-∠C=95°，
∴∠BED=∠BAD=95°，
∴∠CDE=95°-50°=45°，
故选C．
【点拨】本题考查了三角形的内角和，全等三角形的判定和性质，三角形的外角的性质，熟练掌握全等三角形的判定和性质是解题的关键．
9．B
【分析】由SAS证明△AOC≌△BOD，得到∠OAC＝∠OBD，由三角形的外角性质得：∠AMB＋∠OBD＝∠AOB＋∠OAC，得出∠AMB＝∠AOB＝36°，①正确；
根据全等三角形的性质得出∠OCA＝∠ODB，AC＝BD，②正确；
作OG⊥AC于G，OH⊥BD于H，如图所示：则∠OGC＝∠OHD＝90°，由AAS证明△OCG≌△ODH（AAS），得出OG＝OH，由角平分线的判定方法得出MO平分，④正确；
由∠AOB＝∠COD，得出当∠DOM＝∠AOM时，OM才平分∠BOC，假设∠DOM＝∠AOM，由△AOC≌△BOD得出∠COM＝∠BOM，由MO平分∠BMC得出∠CMO＝∠BMO，推出△COM≌△BOM，得OB＝OC，而OA＝OB，所以OA＝OC，而，故③错误；即可得出结论．
解：∵∠AOB＝∠COD＝36°，
∴∠AOB＋∠BOC＝∠COD＋∠BOC，
即∠AOC＝∠BOD，
在△AOC和△BOD中，
，
∴△AOC≌△BOD（SAS），
∴∠OCA＝∠ODB，AC＝BD，②正确；
∴∠OAC＝∠OBD，

由三角形的外角性质得：∠AMB＋∠OBD＝∠AOB＋∠OAC，
∴∠AMB＝∠AOB＝36°，②正确；
作OG⊥AC于G，OH⊥BD于H，如图所示：
则∠OGC＝∠OHD＝90°，
在△OCG和△ODH中，
，
∴△OCG≌△ODH（AAS），
∴OG＝OH，
∴平分，④正确；
∵∠AOB＝∠COD，
∴当∠DOM＝∠AOM时，OM才平分∠BOC，
假设∠DOM＝∠AOM
∵△AOC≌△BOD，
∴∠COM＝∠BOM，
∵MO平分∠BMC，
∴∠CMO＝∠BMO，
在△COM和△BOM中，
，
∴△COM≌△BOM（ASA），
∴OB＝OC，
∵OA＝OB
∴OA＝OC
与矛盾，
∴③错误；
正确的有①②④；
故选B．

【点拨】本题考查了全等三角形的判定与性质、三角形的外角性质、角平分线的判定等知识；证明三角形全等是解题的关键．
10．C
【分析】当GP⊥AB时，GP的值最小，根据尺规作图的方法可知，GB是∠ABC的角平分线，再根据角平分线的性质可知，当GP⊥AB时，GP=CG=1．
解：由题意可知，当GP⊥AB时，GP的值最小，
根据尺规作图的方法可知，GB是∠ABC的角平分线，
∵∠C=90°，
∴当GP⊥AB时，GP=CG=1，
故答案为：C．
【点拨】本题考查了角平分线的尺规作图以及角平分线的性质，难度不大，解题的关键是根据题意得到GB是∠ABC的角平分线，并熟悉角平分线的性质定理．
11．D
【分析】利用基本作图得到AG平分，所以，利用含30度的直角三角形三边的关系得到，根据角平分线的性质得到G点到AM的距离为3，然后对各选项进行判断．
解：由作法得AG平分，
，
，
，
，
∵AG平分，
∴G点到AM的距离为3，
．
故选D．
【点拨】本题考查了作图-基本作图：熟练掌握5种基本作图（作一条线段等于已知线段；作一个角等于已知角；作已知线段的垂直平分线；作已知角的角平分线；过一点作已知直线的垂线）．
12．C
【分析】如图，过点D作于E，根据已知求出CD的长，再根据角平分线的性质进行求解即可.
解：如图，过点D作于E，
，，
，
，BD平分，
，
即点D到AB的距离为2，
故选C．

【点拨】本题考查了角平分线的性质，熟练掌握角平分线上的点到角两边的距离相等是解题的关键.
13．C
【分析】A、由作法得BD是∠ABC的平分线，即可判定；
B、先根据三角形内角和定理求出∠ABC的度数，再由BP是∠ABC的平分线得出∠ABD＝30°＝∠A,即可判定；
C，D、根据含30°的直角三角形，30°所对直角边等于斜边的一半，即可判定.
解：由作法得BD平分∠ABC，所以A选项的结论正确；
∵∠C＝90°，∠A＝30°，
∴∠ABC＝60°，
∴∠ABD＝30°＝∠A，
∴AD＝BD，所以B选项的结论正确；
∵∠CBD＝∠ABC＝30°，
∴BD＝2CD，所以D选项的结论正确；
∴AD＝2CD，
∴S△ABD＝2S△CBD，所以C选项的结论错误．
故选C．

【点拨】此题考查含30°角的直角三角形的性质，尺规作图（作角平分线），解题关键在于利用三角形内角和进行计算.
14．B
【分析】过D作DE⊥AB交BA的延长线于E，根据角平分线的性质得到DE=CD=4，根据三角形的面积公式即可得到结论．
解：如图，过D作DE⊥AB交BA的延长线于E，

∵BD平分∠ABC，∠BCD=90°，
∴DE=CD=4，
∴四边形的面积
故选B.
【点拨】本题考查了角平分线的性质，三角形的面积的计算，正确的作出辅助线是解题的关键．
15．B
【分析】根据AB＝AC可得∠B＝∠C，CD＝DA可得∠ADB＝2∠C＝2∠B，BA＝BD，可得∠BDA＝∠BAD＝2∠B，在△ABD中利用三角形内角和定理可求出∠B．
解：∵AB＝AC，
∴∠B＝∠C，
∵CD＝DA，
∴∠C＝∠DAC，
∵BA＝BD，
∴∠BDA＝∠BAD＝2∠C＝2∠B，
设∠B＝α，则∠BDA＝∠BAD＝2α，
又∵∠B＋∠BAD＋∠BDA＝180°，
∴α＋2α＋2α＝180°，
∴α＝36°，即∠B＝36°，
故选B．
【点拨】本题主要考查等腰三角形的性质，掌握等边对等角是解题的关键，注意三角形内角和定理和方程思想的应用．
16．①②④．
【解析】
试题分析：①在△ACD和△ABE中，∵AC=AB，∠BAC=∠DAE，AD=AE，∴△ACD≌△ABE（SAS），所以①正确；
②∵△ACD≌△ABE，∴CD=BE，∠NCA=∠MBA，又∵M，N分别为BE，CD的中点，∴CN=BM，在△ACN和△ABM中，∵AC=AB，∠ACN=∠ABM，CN=BM，∴△ACN≌△ABM，∴AN=AM，∠CAN∠BAM，∴∠BAC=∠MAN，∵AB=AC，∴∠ACB=∠ABC，∴∠ABC∠AMN，∴△ABC∽△AMN，所以②正确；
③∵AN=AM，∴△AMN为等腰三角形，所以③不正确；
④∵△ACN≌△ABM，∴S△ACN=S△ABM，∵点M、N分别是BE、CD的中点，∴S△ACD=2S△ACN，S△ABE=2S△ABM，∴S△ACD=S△ABE，∵D是AB的中点，∴S△ABC=2S△ACD=2S△ABE，所以④正确；
本题正确的结论有：①②④；故答案为①②④．
考点：相似三角形的判定与性质；全等三角形的判定与性质；等边三角形的判定与性质．
17．②．
【分析】一般三角形全等的判定方法有SSS，SAS，AAS，ASA，据此可逐个对比求解．
解：∵已知，且
∴若添加①，则可由判定≌；
若添加②，则属于边边角的顺序，不能判定≌；
若添加③，则属于边角边的顺序，可以判定≌．
故答案为②．
【点拨】本题考查全等三角形的几种基本判定方法，只要判定方法掌握得牢固，此题不难判断．
18．．
【分析】由全等三角形的判定方法得出①②正确，③不正确
解：底边和顶角对应相等的两个等腰三角形全等；正确；
两边及其中一边上的中线对应相等的两个三角形全等；正确；
斜边和斜边上的中线对应相等的两个直角三角形全等；不正确；
故答案为．
【点拨】本题考查了命题与定理、全等三角形的判定方法；熟练掌握全等三角形的判定方法是解题的关键．
19．或或.
【分析】根据图形可知证明已经具备了一个公共角和一对相等边，因此可以利用ASA、SAS、AAS证明两三角形全等．
解：∵ ，，
∴可以添加 ，此时满足SAS；
添加条件 ，此时满足ASA；
添加条件，此时满足AAS，
故答案为或或；
【点拨】本题考查了全等三角形的判定，是一道开放题，解题的关键是牢记全等三角形的判定方法．
20．
【分析】根据题意得到，反向延长中线至，使得，连接，最后根据三角形三边关系解题．
解：如图，反向延长中线至，使得，连接，
是的内角平分线，




由三角形三边关系可知，



故答案为：．

【点拨】本题考查角平分线的性质、中线的性质、全等三角形的判定与性质、三角形三边关系等知识，是重要考点，难度一般，掌握相关知识是解题关键．
21．12
【分析】根据题意，先证明△ABD≌△AFD，则BD=FD，AB=AF=5，则的周长=BC+CF，即可求出答案．
解：根据题意可知，AD是∠BAC的角平分线，
∴∠BAD=∠FAD，
∵AB=AF=5，AD=AD，
∴△ABD≌△AFD，
∴BD=FD，
∴FD+DC=BD+DC=BC=9，
∵FC=ACAF=85=3，
∴的周长为：FD+DC+FC=9+3=12；
故答案为：12．
【点拨】本题考查了角平分线的性质，全等三角形的判定和性质，解题的关键是掌握作角平分线的方法，以及全等三角形的判定和性质进行解题．
22．27
【分析】由作图步骤可知BG为∠ABC的角平分线，过G作GH⊥BC,GM⊥AB，可得GM=GH
,然后再结合已知条件和三角形的面积公式求得GH，最后运用三角形的面积公式解答即可．
解：由作图作法可知：BG为∠ABC的角平分线
过G作GH⊥BC,GM⊥AB
∴GM=GH
∴,

故答案为27．

【点拨】本题考查了角平分线定理和三角形面积公式的应用，通过作法发现角平分线并灵活应用角平分线定理是解答本题的关键．
23．1 解：延长AD至E，使AD=DE，连接CE，则AE=2m，∵AD是△ABC的中线，∴BD=CD，在△ADB和△EDC中，∵AD=DE，∠ADB=∠EDC，BD=CD，∴△ADB≌△EDC，∴EC=AB=5，在△AEC中，EC﹣AC＜AE＜AC+EC，即5﹣3＜2m＜5+3，∴1＜m＜4，故答案为1＜m＜4．

考点：全等三角形的判定与性质；三角形三边关系．
24．（1）见解析；（2）见解析
【分析】（1）首先以A为圆心，小于AC长为半径画弧，交AC、AB于N、M，再分别以N、M为圆心，大于MN长为半径画弧，两弧交于点Q，再画射线AQ交CB于E；
（2）依据证明得到，进一步可得结论．
解：（1）如图，为所作的平分线；

（2）证明：如图．连接DE，由(1)知：
在和中
∵
∴，
∴
又∵
∴，
∴
【点拨】此题主要考查了基本作图，以及全等三角形的判定和性质，关键是得到．
25．（1）①；（2）证明见解析
【分析】（1）根据作图的过程知道：OM=ON，OC=OC，CM=CM，由“SSS”可以证得△EOC≌△DOC；
（2）根据作图的过程知道：OM=ON，OC=OC，CM=CM，由全等三角形的判定定理SSS可以证得△EOC≌△DOC，从而得到OC为的平分线．
解：（1）根据作图的过程知道：OM=ON，OC=OC，CM=CM，所以由全等三角形的判定定理SSS可以证得△EOC≌△DOC，从而得到OC为的平分线；
故答案为：①；
（2）如图，

连接MC、NC．
根据作图的过程知，
在△MOC与△NOC中，
，
∴△MOC≌△NOC（SSS），
∠AOC=∠BOC，
∴OC为的平分线．
【点拨】本题考查了作图-基本作图及全等三角形的判定定理的应用，注意：三角形全等的判定定理有SAS，ASA，AAS，SSS，HL．
26．见解析
【分析】利用“边角边”证明△ABC和△DEC全等，再根据全等三角形对应边相等解答．
解：证明：在和中，



【点拨】本题考查了全等三角形的应用，熟练掌握三角形全等的判定方法是解题的关键
27．见解析.
【分析】利用SAS证明△ACF≌△BDE，根据全等三角形的性质即可得.
解：∵AE＝BF，
∴AF＝BE，
∵AC∥BD，
∴∠CAF＝∠DBE，
又AC＝BD，
∴△ACF≌△BDE(SAS)，
∴CF＝DE.
【点拨】本题考查了全等三角形的判定与性质，熟练掌握是解题的关键.
28．(1)见解析；（2）
【分析】（1）由角平分线定义得出，由证明即可；
（2）由三角形内角和定理得出，由角平分线定义得出，在中，由三角形内角和定理即可得出答案．
解：（1）证明：平分，
，
在和中，，
；
（2），，
，
平分，
，
在中，．
【点拨】本题考查了全等三角形的判定与性质、角平分线的定义、三角形内角和定理；熟练掌握三角形内角和定理和角平分线定义，证明三角形全等是解题的关键．
29．（1）；（2），理由详见解析.
【分析】（1）先根据角平分线的定义和平行线的性质证得，再根据AAS证得≌，于是，进一步即得结论；
（2）延长交的延长线于点，如图②，先根据AAS证明≌，可得，再根据角平分线的定义和平行线的性质证得，进而得出结论.
解：（1）.
理由如下：如图①，∵是的平分线，∴
∵，∴，∴，∴.
∵点是的中点，∴，
又∵，
∴≌（AAS），∴.
∴.
故答案为.
（2）.
理由如下：如图②，延长交的延长线于点.

∵，∴，
又∵，，
∴≌（AAS），∴，
∵是的平分线，∴，
∵，∴，∴，
∵，∴.
【点拨】本题考查了全等三角形的判定和性质、平行线的性质、角平分线的定义和等角对等边等知识，添加恰当辅助线构造全等三角形是解本题的关键．