专题22.17 二次函数与一元二次方程（专项练习1）-2021-2022学年九年级数学上册基础知识专项讲练（人教版）

这是一份专题22.17 二次函数与一元二次方程（专项练习1）-2021-2022学年九年级数学上册基础知识专项讲练（人教版），共28页。试卷主要包含了抛物线，二次函数图象与y轴的交点坐标是等内容，欢迎下载使用。
专题22.17 二次函数与一元二次方程（专项练习1）
一、 单选题

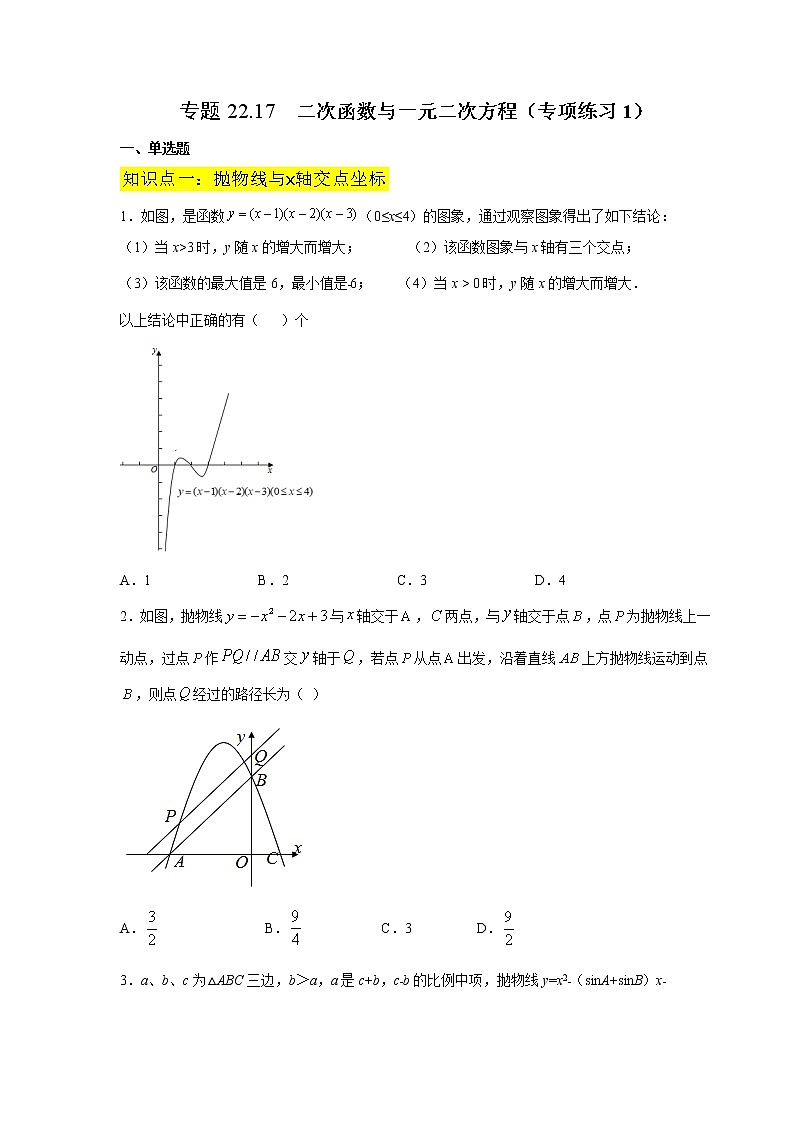
1．如图，是函数（0≤x≤4）的图象，通过观察图象得出了如下结论：
（1）当x>3时，y随x的增大而增大； （2）该函数图象与x轴有三个交点；
（3）该函数的最大值是6，最小值是﹣6； （4）当x > 0时，y随x的增大而增大．
以上结论中正确的有（ ）个

A．1 B．2 C．3 D．4
2．如图，抛物线与轴交于，两点，与轴交于点，点为抛物线上一动点，过点作交轴于，若点从点出发，沿着直线上方抛物线运动到点，则点经过的路径长为（ ）

A． B． C．3 D．
3．a、b、c为△ABC三边，b＞a，a是c+b，c﹣b的比例中项，抛物线y=x2﹣（sinA+sinB）x﹣（a+b+c）的对称轴是x=，交y轴于（0，﹣30），则方程ax2﹣cx+b=0的根的情况是（　　）
A．有两不等实根 B．有两相等实根
C．无实根 D．以上都不对

4．抛物线（m是常数）与坐标轴交点的个数为（ ）
A．0 B．1 C．2或3 D．3
5．二次函数图象与y轴的交点坐标是（ ）
A． B． C． D．
6．已知二次函数y＝ax2﹣4ax+3与x轴交于A、B两点，与y轴交于点C，若S△ABC＝3，则a＝（　　）
A． B． C．﹣1 D．1

7．如表是二次函数y＝ax2+bx+c的几组对应值：
x
6.17
6.18
6.19
6.20
y＝ax2+bx+c
﹣0.03
﹣0.01
0.02
0.04
根据表中数据判断，方程ax2+bx+c＝0的一个解x的范围是（　　）
A．6＜x＜6.17 B．6.17＜x＜6.18
C．6.18＜x＜6.19 D．6.19＜x＜6.20
8．已知二次函数的自变量与函数的部分对应值列表如下：

…

0
1
2
3
…

…
3
0


3
…
则关于的方程的解是（ ）
A．， B．
C． D．不能确定
9．二次函数y＝ax2+bx+c的部分对应值如表：

利用该二次函数的图象判断，当函数值y＞0时，x的取值范围是（ ）
A．0＜x＜8 B．x＜0或x＞8 C．﹣2＜x＜4 D．x＜﹣2或x＞4

10．如表是一组二次函数y＝x2﹣x﹣3的自变量和函数值的关系，那么方程x2﹣x﹣3＝0的一个近似根是（ ）
x
1
2
3
4
y
﹣3
﹣1
3
9
A．1.2 B．2.3 C．3.4 D．4.5
11．已知二次函数y＝ax2+bx+c与自变量x的部分对应值如表，下列说法错误的是（　　）
x
…
﹣1
0
1
3
…
y
…
﹣3
1
3
1
…
A．a＜0
B．方程ax2+bx+c＝﹣2的正根在4与5之间
C．2a+b＞0
D．若点（5，y1）、（﹣，y2）都在函数图象上，则y1＜y2
12．下表是满足二次函数y＝ax2＋bx＋c的五组数据，x1是方程ax2＋bx＋c＝0的一个解，则下列选项中正确的是（ ）
x
1.6
1.8
2.0
2.2
2.4
y
－0.80
－0.54
－0.20
0.22
0.72

A．1.6＜x1＜1.8 B．2.0＜x1＜2.2 C．1.8＜x1＜2.0 D．2.2＜x1＜2.4

13．如图是二次函数的部分图象，由图象可知不等式的解集是（ ）

A． B． C．且 D．x＜－1或x＞5
14．如图，已知二次函数的图象与正比例函数的图象交于点A（3，2），与x轴交于点B（2，0），若，则x的取值范围是（ ）

A．0＜x＜2 B．0＜x＜3 C．2＜x＜3 D．x＜0或x＞3
15．如图是二次函数y＝ax2+bx+c的部分图象，y0时自变量x的取值范围是（　　）

A．﹣1x5 B．x﹣1或 x5
C．x﹣1且x5 D．x﹣1或x5

二、 填空题

16．已知，，满足，，则二次函数的图象的对称轴为_______．
17．已知抛物线与轴的一个交点的横坐标大于1且小于2，则m的取值范围是________．
18．已知抛物线与x轴交于A、B两点（点A在点B左侧），则线段的长为______．

19．若函数的图像与坐标轴有三个交点，则c的取值范围是________．
20．抛物线与y轴的交点坐标为__________．
21．抛物线与轴的交点坐标是______．
22．抛物线y=x2+2x﹣2018过点（m，0），则代数式m2+2m+1=_____．

23．已知二次函数y＝ax2＋bx＋c（a≠0）中，函数值y与自变量x的部分对应值如下表：
x
…
﹣5
﹣4
﹣3
﹣2
﹣1
…
y
…
0
﹣2
﹣5
﹣6
﹣5
…
则关于x的一元二次方程ax2＋bx＋c＝﹣2的根是_____．
24．已知：二次函数图象上部分点的横坐标与纵坐标的对应值如下表所示，那么方程（，，，为常数）的根是________．

…
-1
0
1
2
3

…
0
3
4
3
0

25．二次函数（a≠0，a，b，c是常数）中，自变量x与函数y的对应值如下表：
x
-1
-
0

1

2

3
y
-2

1

2

1

-2
一元二次方程（a≠0，a，b，c是常数）的两个根的取值范围是下列选项中的哪一个 ______ （填序号）
① ②
③ ④

26．如图，二次函数y＝ax2+bx+c的图象过点A(3，0)，对称轴为直线x＝1，给出以下结论：①abc＜0；②a+b+c≥ax2+bx+c；③若为函数图象上的两点，则y1＜y2；④若关于x的一元二次方程ax2+bx+c＝p（p＞0）有整数根，则p的值有2个．其中正确的有___．

27．二次函数的图象如图所示，若方程的一个近似根是，则方程的另一个近似根为__________．（结果精确到0.1）



28．如图所示，抛物线y=ax2+bx+c（a0）与轴的两个交点分别为A（-1，0）和B（2，0），当y＜0时，x的取值范围是___________．


29．二次函数y＝﹣x2+bx+c的部分图象如图所示，由图象可知，不等式﹣x2+bx+c＜0的解集为______．

30．二次函数y＝ax2＋bx＋c（a≠0）的图像如图所示，当y＜3时，x的取值范围是____．


三、 解答题

31．已知二次函数的图象经过点和．
（1）求这个二次函数的表达式；
（2）求出函数图象与坐标轴的交点．





32．已知二次函数y＝﹣x2﹣2x+3．
（1）求这个二次函数图象的顶点坐标．
（2）求这个二次函数图象与x轴的交点坐标．
（3）直接写出这个二次函数图象与y轴的交点坐标　 　．


33．已知二次函数的图象经过点P（﹣3，1），对称轴是直线 ．
（1）求m、n的值；
（2）如图，一次函数y=kx+b的图象经过点P，与x轴相交于点A，与二次函数的图象相交于另一点B，点B在点P的右侧，PA：PB=1：5，求一次函数的表达式．



34．小帆同学根据函数的学习经验，对函数进行探究，已知函数过，，．
（1）求函数解析式；
（2）如图1，在平面直角坐标系中画的图象，根据函数图象，写出函数的一条性质　　　　；
（3）结合函数图象回答下列问题：
①方程的近似解的取值范围(精确到个位)是　　　　；
②若一次函数与有且仅有两个交点，则的取值范围是　　　　．





35．二次函数y＝ax2+bx+c的图象如图所示，经过（﹣1，0）、（3，0）、（0，﹣3）．
（1）求二次函数的解析式；
（2）不等式ax2+bx+c＞0的解集为　 　；
（3）方程ax2+bx+c＝m有两个实数根，m的取值范围为　 　．


参考答案
1．C
【分析】
根据函数图象的性质进行逐项分析即可．
解：由题中图象可知，该函数图象与x轴有三个交点，故（2）正确；
令，
解得：，，，
即该函数图象与x轴的三个交点坐标分别为，，，
∴结合图形可知，当x>3时，y随x的增大而增大，故（1）正确；
∵自变量的范围是0≤x≤4，
∴结合图象可知，当时，函数取得最大值，最大值为，
当时，函数取得最小值，最小值为，故（3）正确；
由图象可知，当x > 0时，函数图象既有上升的部分，也有下降的部分，
∴在x > 0时，增减性不是唯一的，故（4）错误；
故选：C．
【点拨】本题考查函数图象的性质，掌握函数图象与坐标轴的交点的求法与意义，理解判断函数性质的方法是解题关键．
2．D
【分析】分别求出A，B的坐标，运用待定系数法求出直线AB，PQ的解析式，再求出它们与y轴的交点坐标即可解决问题．
解：对于，
令x=0，则y=3，
∴
令y=0，则
解得，
∵点A在点C的左侧，
∴A（-3，0）
设AB所在直线解析式为，
把A，B点坐标代入得，解得
所以，直线AB的解析式为：y=x+3，
∵PQ//AB
∴设PQ的解析式为：y=x+a
∵点经过的路径长是直线PQ经过抛物线的切点与y轴的交点和点B的距离的2倍，
∴方程有两个相等的实数根，
∴
解得，
∴点Q的坐标为（0，）
当点P与点A重合时，点Q与点B重合，此时点Q的坐标为（0，3）
点经过的路径长为
故选：D．

【点拨】本题考查的是抛物线与x轴的交点，主要考查函数图象上点的坐标特征，要求学生非常熟悉函数与坐标轴的交点的求法．
3．C
【分析】首先证明△ABC是直角三角形，想办法求出a，b，c的值，利用判别式即可解决问题．
解：∵a是c+b，c﹣b的比例中项，
∴a2=（c+b）（c﹣b），
∴a2=c2﹣b2，
∴a2+b2=c2①
∴∠C=90°，
∴△ABC是直角三角形，
∴sinA+sinB=，
由题意：，
解得c=13，
a+b=17 ②，
由①②，
∵b＞a，可得a=5，b=12，
对于方程ax2﹣cx+b=0，
=c2﹣4ab=169﹣4×12×5=﹣71＜0，
∴方程没有实数根，
故选：C．
【点拨】本题考查抛物线与x轴的交点、根的判别式、比例线段、解直角三角形、二次函数图象与系数的关系．
4．C
【分析】先计算判别式的值可判断抛物线与x轴的交点个数，而抛物线与y轴一定有一个交点，再讨论是否有重合的点，可得结果．
解：令，
则，
∴抛物线与x轴有2个公共点，
∵x=0时，y=，
若m=±1，则抛物线与y轴交于原点，
此时抛物线与坐标轴有2个交点，
若m≠±1，则抛物线与y轴交于（0，），
此时抛物线与坐标轴有3个交点，
故选C．
【点拨】本题考查了抛物线与x轴的交点：对于二次函数y=ax2+bx+c（a，b，c是常数，a≠0），△=b2-4ac决定抛物线与x轴的交点个数：△=b2-4ac＞0时，抛物线与x轴有2个交点；△=b2-4ac=0时，抛物线与x轴有1个交点；△=b2-4ac＜0时，抛物线与x轴没有交点，同时也考查了抛物线与y轴的交点．
5．D
【分析】根据y轴上点的坐标特征，计算自变量为0时的函数值即可得到交点坐标．
解：根据题意，
令，则，
∴二次函数图象与y轴的交点坐标是；
故选：D．
【点拨】本题考查了二次函数图象上点的坐标特征：二次函数图象上点的坐标满足其解析式．
6．D
【分析】由根与系数的关系求得AB的长度，由抛物线解析式求得点C的坐标，然后根据列出关于的方程，解方程即可
令，则ax2﹣4ax+3＝0，
∴x1+x2＝4，x1•x2＝，
∴AB＝|x1﹣x2|＝，
令x＝0，y＝3，
∴OC＝3，
∴S△ABC＝AB•OC＝，
∴．
故选：D．
【点拨】本题考查了二次函数与坐标轴交点的问题，一元二次方程根与系数的关系，熟练掌握一元二次方程跟与系数的关系是解题关键．
7．C
【分析】由x=6.18时，y=-0.010，根据函数的连续性知，6.18