2020-2021学年云南省昆明市官渡区九年级（上）期末数学试卷

2020-2021学年云南省昆明市官渡区九年级（上）期末数学试卷

一、填空题（每题3分，共18分）

1．（3分）若方程是关于的一元二次方程，则的取值范围是　　．

2．（3分）若点在二次函数的图象上，则　　．

3．（3分）为了解今年从西伯利亚飞到昆明过冬的红嘴鸥的数量，某研究团队给200只红嘴鸥做上标记，经过一段时间，当带有标记的红嘴鸥和其它不带标记的红嘴鸥完全混合后，再次观察发现416只红嘴鸥中有2只带有标记，那么由此可以估计今年飞到昆明过冬的红嘴鸥大约有　　只．

4．（3分）如图，沿一条母线将圆锥侧面剪开并展平，得到一个扇形，若圆锥的底面圆的半径，扇形的圆心角，则该圆锥的母线长为　　．

5．（3分）如图，在平面直角坐标系中，正六边形的边长是2，则它的外接圆圆心的坐标是　　．

6．（3分）如图，，分别与相切于点，点，，是上异于，的点，则的度数为　　．

二、选择题（每题4分，共32分）

7．（4分）下面的图形是用数学家名字命名的，其中既是轴对称图形又是中心对称图形的是　　

A．赵爽弦图 B．科克曲线 

C．笛卡尔心形线 D．斐波那契螺旋线

8．（4分）关于的方程的一个根是3，则它的另一个根是　　

A． B．0 C．1 D．2

9．（4分）下列说法不正确的是　　

A．“三角形任意两边之和小于第三边”是不可能事件 

B．“篮球队员在罚球线上投篮一次，投中”为随机事件 

C．某种彩票的中奖率是，说明每买100张彩票，一定有1张中奖 

D．“在同一年出生的367人中，至少有两人的生日相同”是必然事件

10．（4分）下列一元二次方程没有实数根的是　　

A． B． C． D．

11．（4分）抛物线经过平移得到抛物线，平移的方法是　　

A．向左平移1个，再向下平移2个单位 

B．向右平移1个，再向下平移2个单位 

C．向左平移1个，再向上平移2个单位 

D．向右平移1个，再向上平移2个单位

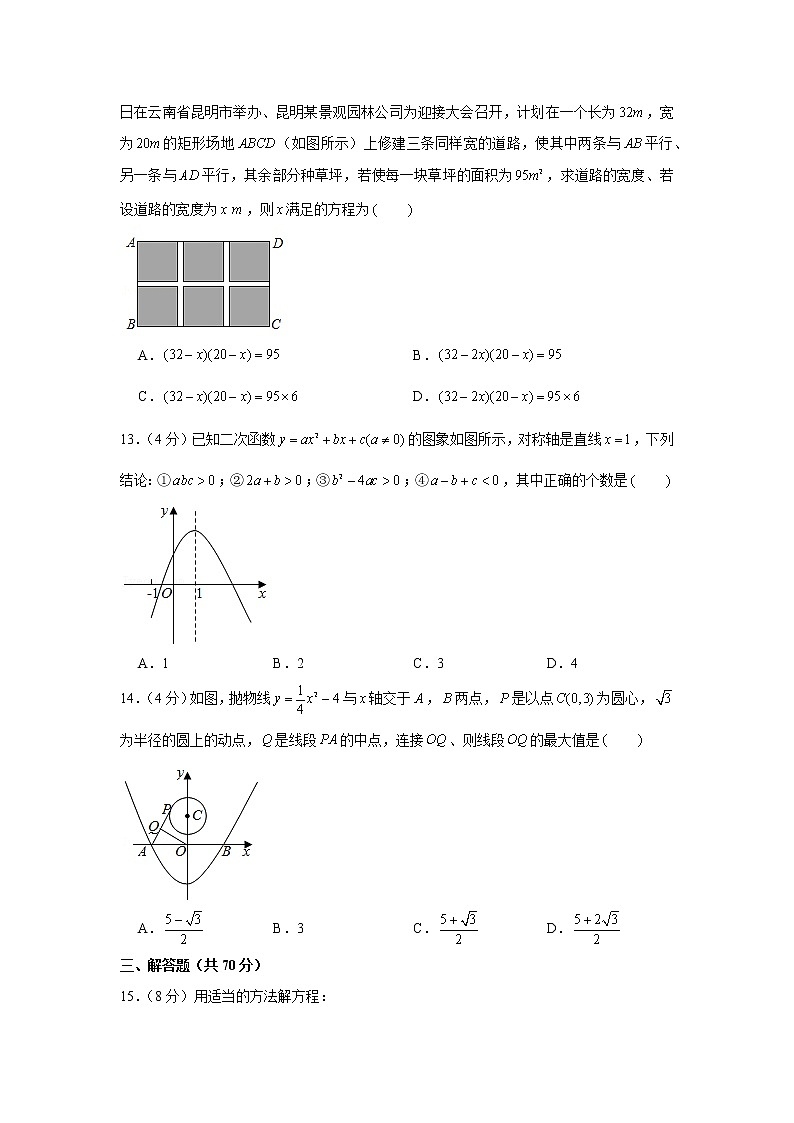
12．（4分）《生物多样性公约》第十五次缔约方大会将于2021年5月17日至30日在云南省昆明市举办、昆明某景观园林公司为迎接大会召开，计划在一个长为，宽为的矩形场地（如图所示）上修建三条同样宽的道路，使其中两条与平行、另一条与平行，其余部分种草坪，若使每一块草坪的面积为，求道路的宽度、若设道路的宽度为，则满足的方程为　　

A． B． 

C． D．

13．（4分）已知二次函数的图象如图所示，对称轴是直线，下列结论：①；②；③；④，其中正确的个数是　　

A．1 B．2 C．3 D．4

14．（4分）如图，抛物线与轴交于，两点，是以点为圆心，为半径的圆上的动点，是线段的中点，连接、则线段的最大值是　　

A． B．3 C． D．

三、解答题（共70分）

15．（8分）用适当的方法解方程：

（1）；

（2）．

16．（8分）如图，三个顶点坐标分别为，，．

（1）请画出关于原点中心对称的图形△，并直接写出点的坐标；

（2）请画出绕原点逆时针旋转的图形△，并直接写出点的坐标；

（3）求在（2）的旋转过程中，点旋转到所经过的路径长（结果保留．

17．（6分）2020年9月29日，国家卫健委新闻发言人米锋在发布会上表示，疫情仍在全球扩散蔓延，但我国疫情已得到有效控制．新冠肺炎具有人传人的特性，若一人携带病毒，未进行有效隔离，经过两轮传染后共有169人患新冠肺炎（假设每轮传染的人数相同）．

（1）每轮传染中平均每个人传染了几个人？

（2）如果这169位病毒携带者，未进行有效隔离，按照这样的传染速度，第三轮传染后，共有多少人患病？

18．（6分）如图，在中，，，点在上，将绕点顺时针方向旋转后，得到．

（1）求的度数；

（2）若，，求的长．

19．（6分）如图，内接于，是上的一点，连接，，．

（1）求证：；

（2）若，，求的半径．

20．（8分）为了让广大学子通过身边的故事，深刻感受伟大祖国“十三五”时期的发展建设成就，畅想未来美好蓝图，由教育部组织的“我和我的学校”网络微视频接力活动于近期启动，活动分为两个阶段，第一阶段以“记住这些年”为主题，第二阶段以“追梦2035”为主题．昆明某校学生准备从4个不同的素材，，，中选取一个参加第一阶段的主题活动，从3个不同的素材，，中选取一个参加第二阶段的主题活动．现将这两个阶段的7个素材分别写在形状大小质地都相同的卡片上．

（1）如果把所有卡片混在一起，张月同学一次抽中第二阶段活动素材的概率是　　．

（2）李华同学对第一阶段的素材，和第二阶段的素材，准备得较好，如果第一次抽签确定第一阶段活动内容，第二次抽签确定第二阶段活动内容．请用列表或画树状图的方法，求他抽到的两个素材都准备得较好的概率．

21．（8分）昆明斗南花卉市场是全国鲜花市场的心脏，也是亚洲最大的鲜花交易市场之一．斗南某兰花专卖店专门销售某种品牌的兰花，已知这种兰花的成本价为60元盆．市场管理部门规定：每盆兰花的销售价格不低于成本价，又不高于成本价的2倍．经过市场调查发现，该店某天的销售数量（盆与销售单价（元盆）之间的函数关系如图所示：

（1）求与之间的函数关系式，并写出自变量的取值范围；

（2）在销售过程中，该店每天还要支付其他费用200元，求这一天销售兰花获得的利润（元的最大值．

22．（8分）如图，是的直径，点和点是上的两点，连接，，，过点作射线交的延长线于点，使．

（1）求证：是的切线；

（2）若，求阴影部分的面积．

23．（12分）如图①，抛物线与轴交于，两点，与轴交于点．

（1）求抛物线的解析式；

（2）如图②，连接，点是第四象限内抛物线上的动点，过点作于点，轴交于点，求面积的最大值及此时点的坐标；

（3）如图③，若抛物线的顶点坐标为点，点是抛物线对称轴上的动点，在坐标平面内是否存在点，使得以，，，为顶点的四边形是菱形？若存在，求出点的坐标；若不存在，请说明理由．

2020-2021学年云南省昆明市官渡区九年级（上）期末数学试卷

参考答案与试题解析

一、填空题（每题3分，共18分）

1．（3分）若方程是关于的一元二次方程，则的取值范围是　　．

【解答】解：方程是关于的一元二次方程，

，

故答案为：．

2．（3分）若点在二次函数的图象上，则　4　．

【解答】解：将点代入得：．

故答案为：4．

3．（3分）为了解今年从西伯利亚飞到昆明过冬的红嘴鸥的数量，某研究团队给200只红嘴鸥做上标记，经过一段时间，当带有标记的红嘴鸥和其它不带标记的红嘴鸥完全混合后，再次观察发现416只红嘴鸥中有2只带有标记，那么由此可以估计今年飞到昆明过冬的红嘴鸥大约有　41600　只．

【解答】解：

（只，

即估计今年飞到昆明过冬的红嘴鸥大约有41600只，

故答案为：41600．

4．（3分）如图，沿一条母线将圆锥侧面剪开并展平，得到一个扇形，若圆锥的底面圆的半径，扇形的圆心角，则该圆锥的母线长为　9　．

【解答】解：圆锥的底面周长，

设圆锥的母线长为，则：，

解得．

故答案为：9．

5．（3分）如图，在平面直角坐标系中，正六边形的边长是2，则它的外接圆圆心的坐标是　　．

【解答】解：连接，，

正六边形的外接圆心是，

，，

是等边三角形，

，

过作于，则，，

，

的坐标是，

故答案为：．

6．（3分）如图，，分别与相切于点，点，，是上异于，的点，则的度数为　或　．

【解答】解：如图，

、分别切于点、，

则；

在四边形中，，

①当点在优弧上时，（同弧所对的圆周角是所对的圆心角的一半），

；

当点在劣弧上时，记作，

由①知，，

四边形是的内接四边形，

，

故答案为：或．

二、选择题（每题4分，共32分）

7．（4分）下面的图形是用数学家名字命名的，其中既是轴对称图形又是中心对称图形的是　　

A．赵爽弦图 B．科克曲线 

C．笛卡尔心形线 D．斐波那契螺旋线

【解答】解：、不是轴对称图形，是中心对称图形，故此选项不合题意；

、既是中心对称图形又是轴对称图形，故此选项符合题意；

、是轴对称图形，不是中心对称图形，故此选项不合题意；

、既不是轴对称图形，也不是中心对称图形，故此选项不合题意．

故选：．

8．（4分）关于的方程的一个根是3，则它的另一个根是　　

A． B．0 C．1 D．2

【解答】解：设方程的另一个根是，

由根与系数的关系可知：，

解得，

所以，它的另一个根是．

故选：．

9．（4分）下列说法不正确的是　　

A．“三角形任意两边之和小于第三边”是不可能事件 

B．“篮球队员在罚球线上投篮一次，投中”为随机事件 

C．某种彩票的中奖率是，说明每买100张彩票，一定有1张中奖 

D．“在同一年出生的367人中，至少有两人的生日相同”是必然事件

【解答】解：、“三角形任意两边之和小于第三边”是不可能事件，本选项说法正确，不符合题意；

、“篮球队员在罚球线上投篮一次，投中”为随机事件，本选项说法正确，不符合题意；

、某种彩票的中奖率是，说明每买100张彩票，不一定有1张中奖，本选项说法不正确，符合题意；

、“在同一年出生的367人中，至少有两人的生日相同”是必然事件，本选项说法正确，不符合题意；

故选：．

10．（4分）下列一元二次方程没有实数根的是　　

A． B． C． D．

【解答】解：、方程的实数根为，所以选项不符合题意；

、方程的实数根为或，所以选项不符合题意；

、△，则方程有两个不相等的实数根，所以选项不符合题意；

、△，则方程无实数根，所以选项符合题意．

故选：．

11．（4分）抛物线经过平移得到抛物线，平移的方法是　　

A．向左平移1个，再向下平移2个单位 

B．向右平移1个，再向下平移2个单位 

C．向左平移1个，再向上平移2个单位 

D．向右平移1个，再向上平移2个单位

【解答】解：抛物线的顶点坐标为，抛物线的顶点坐标为，

而点向左平移1个，再向下平移2个单位可得到，

所以抛物线向左平移1个，再向下平移2个单位得到抛物线．

故选：．

12．（4分）《生物多样性公约》第十五次缔约方大会将于2021年5月17日至30日在云南省昆明市举办、昆明某景观园林公司为迎接大会召开，计划在一个长为，宽为的矩形场地（如图所示）上修建三条同样宽的道路，使其中两条与平行、另一条与平行，其余部分种草坪，若使每一块草坪的面积为，求道路的宽度、若设道路的宽度为，则满足的方程为　　

A． B． 

C． D．

【解答】解：设道路的宽度为，则六块草坪可合成长，宽的矩形，

依题意得：．

故选：．

13．（4分）已知二次函数的图象如图所示，对称轴是直线，下列结论：①；②；③；④，其中正确的个数是　　

A．1 B．2 C．3 D．4

【解答】解：函数图象开口向下，对称轴为，与轴的交点在轴正半轴上，

，，，，

，，故①②错误，不符合题意；

由图象可知：函数图象与轴有两个交点，当时，，

，，故③④正确，符合题意．

故选：．

14．（4分）如图，抛物线与轴交于，两点，是以点为圆心，为半径的圆上的动点，是线段的中点，连接、则线段的最大值是　　

A． B．3 C． D．

【解答】解：连接，如图，

当时，，解得，，则，，

是线段的中点，

为的中位线，

，

当最大时，最大，

而过圆心时，最大，如图，

，

的最大值，

线段的最大值是．

故选：．

三、解答题（共70分）

15．（8分）用适当的方法解方程：

（1）；

（2）．

【解答】解：（1），

，即，

则，

，

则，；

（2），

，

则或，

解得，．

16．（8分）如图，三个顶点坐标分别为，，．

（1）请画出关于原点中心对称的图形△，并直接写出点的坐标；

（2）请画出绕原点逆时针旋转的图形△，并直接写出点的坐标；

（3）求在（2）的旋转过程中，点旋转到所经过的路径长（结果保留．

【解答】解：（1）如图所示，△即为所求，点的坐标为．

（2）如图所示，△即为所求，点的坐标为．

（3）根据题意可知，，点旋转到所经过的路径长为：．

17．（6分）2020年9月29日，国家卫健委新闻发言人米锋在发布会上表示，疫情仍在全球扩散蔓延，但我国疫情已得到有效控制．新冠肺炎具有人传人的特性，若一人携带病毒，未进行有效隔离，经过两轮传染后共有169人患新冠肺炎（假设每轮传染的人数相同）．

（1）每轮传染中平均每个人传染了几个人？

（2）如果这169位病毒携带者，未进行有效隔离，按照这样的传染速度，第三轮传染后，共有多少人患病？

【解答】解：（1）设每轮传染中平均每个人传染了个人，

依题意得：，

解得：，（不合题意，舍去）．

答：每轮传染中平均每个人传染了12个人．

（2）（人．

答：按照这样的传染速度，第三轮传染后，共有2197人患病．

18．（6分）如图，在中，，，点在上，将绕点顺时针方向旋转后，得到．

（1）求的度数；

（2）若，，求的长．

【解答】解：（1）在中，，，

，

由旋转的性质可知，

．

（2），，

，

，

，．

由旋转的性质可知：．

在中，，

．

19．（6分）如图，内接于，是上的一点，连接，，．

（1）求证：；

（2）若，，求的半径．

【解答】（1）证明：，

，

，

；

（2）如图：连接，，过点作于点，

，

，

，

，，

，

，

．

设为，则为，

，

，

解得，

，

的半径为．

20．（8分）为了让广大学子通过身边的故事，深刻感受伟大祖国“十三五”时期的发展建设成就，畅想未来美好蓝图，由教育部组织的“我和我的学校”网络微视频接力活动于近期启动，活动分为两个阶段，第一阶段以“记住这些年”为主题，第二阶段以“追梦2035”为主题．昆明某校学生准备从4个不同的素材，，，中选取一个参加第一阶段的主题活动，从3个不同的素材，，中选取一个参加第二阶段的主题活动．现将这两个阶段的7个素材分别写在形状大小质地都相同的卡片上．

（1）如果把所有卡片混在一起，张月同学一次抽中第二阶段活动素材的概率是　　．

（2）李华同学对第一阶段的素材，和第二阶段的素材，准备得较好，如果第一次抽签确定第一阶段活动内容，第二次抽签确定第二阶段活动内容．请用列表或画树状图的方法，求他抽到的两个素材都准备得较好的概率．

【解答】解：（1）共有7个素材，第一阶段有4个不同的素材，第二阶段有3个不同素材，

张月同学一次抽中第二阶段活动素材的概率是．

故答案为：．

（2）根据题意列表如下：

共有12种结果，且每种结果发生的可能性相同，其中李华抽到的两个素材都准备得较好的结果有4种，即，，，，

则他抽到的两个素材都准备得较好的概率是．

21．（8分）昆明斗南花卉市场是全国鲜花市场的心脏，也是亚洲最大的鲜花交易市场之一．斗南某兰花专卖店专门销售某种品牌的兰花，已知这种兰花的成本价为60元盆．市场管理部门规定：每盆兰花的销售价格不低于成本价，又不高于成本价的2倍．经过市场调查发现，该店某天的销售数量（盆与销售单价（元盆）之间的函数关系如图所示：

（1）求与之间的函数关系式，并写出自变量的取值范围；

（2）在销售过程中，该店每天还要支付其他费用200元，求这一天销售兰花获得的利润（元的最大值．

【解答】解：（1）设与之间的函数关系式为，

该函数图象过点，，

，

解得，

与之间的函数关系式为，

每盆兰花的销售价格不低于成本价，又不高于成本价的2倍．

，

由上可得，与之间的函数关系式为；

（2）根据题意，得，

，

当时，有最大值，此时．

答：这一天销售兰花获得的利润的最大值为1400元．

22．（8分）如图，是的直径，点和点是上的两点，连接，，，过点作射线交的延长线于点，使．

（1）求证：是的切线；

（2）若，求阴影部分的面积．

【解答】（1）证明：如图，连接，过点作于点，

则，

，

，，

，

又，

，

，

，

，

，

，

点在上，即是半径，

是的切线；

（2）解：，

，

，

，

，

，

又，

，，

是等边三角形，

，，

，

在中，由勾股定理得：，

，，

．

23．（12分）如图①，抛物线与轴交于，两点，与轴交于点．

（1）求抛物线的解析式；

（2）如图②，连接，点是第四象限内抛物线上的动点，过点作于点，轴交于点，求面积的最大值及此时点的坐标；

（3）如图③，若抛物线的顶点坐标为点，点是抛物线对称轴上的动点，在坐标平面内是否存在点，使得以，，，为顶点的四边形是菱形？若存在，求出点的坐标；若不存在，请说明理由．

【解答】解：（1）将，代入抛物线，

得，

解得，

抛物线的解析式为；

（2）令，则，

，

设直线的解析式为，

将，代入，

得，

解得，

直线的解析式为，

设，，

，

，，

是等腰直角三角形，

，

轴，

，

，

，

是等腰直角三角形，

，

在中，，

，

，

当最大时，的面积最大，

，

当时，的最大值为，

的最大面积，

此时，，；

（3）存在，理由如下：

抛物线，

顶点的坐标为，

，

，

设，则，，

以，，，为顶点的四边形为菱形，有以下三种情况：

①当时，则，

或；

②当时，则，

解得，

；

③当时，则，

解得，（舍，

；

综上所述，满足条件的点有4个，坐标分别为或或或；

声明：试题解析著作权属菁优网所有，未经书面同意，不得复制发布

日期：2021/12/13 10:30:02；用户：初中数学1；邮箱：jse032@xyh.com；学号：39024122