贵州省贵阳市2017届高三上学期期末监测考试数学（文）含答案

这是一份贵州省贵阳市2017届高三上学期期末监测考试数学（文）含答案，共10页。试卷主要包含了设P=，Q=，则，复数的虚部为，等差数列的前项和为，且，则，050，635等内容，欢迎下载使用。
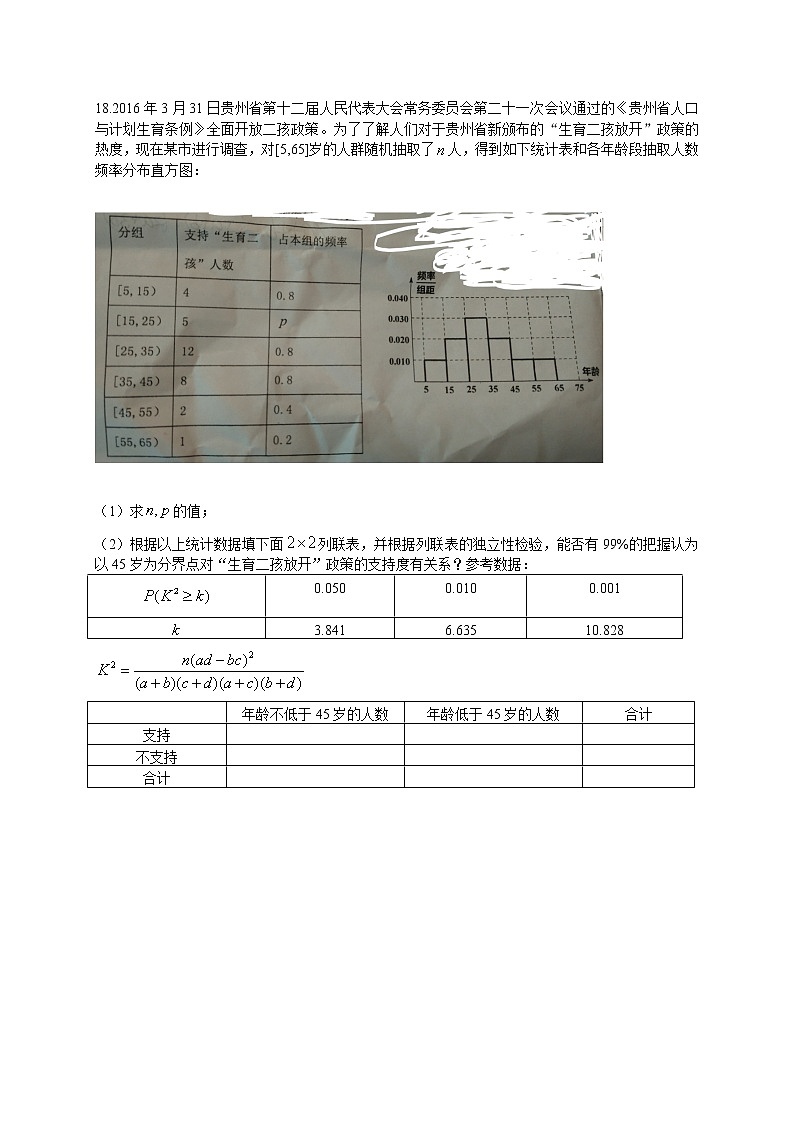
贵阳市普通高中2017届高三年级第一学期期末监测考试试卷高三数学（文科）一．选择题1.设P=，Q=，则（    ）A.PQ    B.QP    C.PCRQ    D.QCRP2.复数的虚部为（    ）A.    B.    C.8    D.-83.等差数列的前项和为，且，则（    ）A.88    B.48    C.96    D.176已知，则（    ）A.    B.    C.    D.设向量，则“”是“”的（    ）充分不必要条件    B.必要不充分条件    C.充要条件    D.既不充分也不必要条件已知角的始边与轴的非负半轴重合，终边过点M（-3,4），则的值为（    ）    B.    C.    D.一个几何体的三视图如图所示，其中正视图是边长为2的等边三角形，俯视图为正六边形，则该几何体的体积是（    ）    B.1    C.2    D.双曲线的两条渐近线将平面划分为“上、下、左、右”四个区域（不含边界），若点（2,1）在“右”区域内，则双曲线离心率的取值范围是（    ）    B.    C.    D.三棱锥P-ABC的四个顶点都在体积为的球的表面上，底面ABC所在的小圆面积为，则该三棱锥的高的最大值为（    ）A.4    B.6    C.8    D.10已知的最小正周期为，若其图象向左平移个单位后关于轴对称，则（    ）    B.    C.    D.正项等比数列中，存在两项，使得，且，则的最小值是（    ）    B.2    C.     D.函数，若恒成立，则实数的取值范围是（    ）A.    B.    C.    D.二．填空题某高校有正教授120人，副教授100人，讲师80人，助教60人，现用分层抽样的方法从以上所有老师中抽取一个容量为的样本，已知从讲师中抽取人数为16人，那么      辗转相除法，又名欧几里得算法，乃求两个正整数之最大公因子的算法。它是已知最古老的算法，在中国则可以追溯至东汉出现的《九章算术》，图中的程序框图所表述的算法就是欧几里得辗转相除法，若输入，则输出的       过抛物线的焦点且倾斜角为600的直线被圆截得的弦长是        若点P在函数的图象上，点Q在函数的图象上，则|PQ|的最小值为    三．解答题在ΔABC中，内角A、B、C的对边长分别为，若（1）求角A的大小；（2）若，求BC边上的中线AM的最大值          18.2016年3月31日贵州省第十二届人民代表大会常务委员会第二十一次会议通过的《贵州省人口与计划生育条例》全面开放二孩政策。为了了解人们对于贵州省新颁布的“生育二孩放开”政策的热度，现在某市进行调查，对[5,65]岁的人群随机抽取了人，得到如下统计表和各年龄段抽取人数频率分布直方图： （1）求的值；（2）根据以上统计数据填下面列联表，并根据列联表的独立性检验，能否有99%的把握认为以45岁为分界点对“生育二孩放开”政策的支持度有关系？参考数据：0.0500.0100.0013.8416.63510.828 年龄不低于45岁的人数年龄低于45岁的人数合计支持   不支持   合计               如图所示，该几何体是一个由直三棱柱ADE-BCF和一个正四棱锥P-ABCD组合而成，AD⊥AF，AE=AD=2（1）证明：平面PAD⊥平面ABFE；（2）若正四棱锥P-ABCD的体积是三棱锥P-ABF体积的4倍，求正四棱锥P-ABCD的高   设椭圆C1的中心和抛物线C2的顶点均为原点O，C1、C2的焦点均在轴上，在C1、C2上各取两个点，将其坐标记录于表格中：（1）求C1、C2的标准方程；（2）过C2的焦点F作斜率为的直线，与C2交于A、B两点，若与C1交于C、D两点，若，求直线的方程3-240-4 已知函数（1）求的单调区间；（2）求函数在上的最大值和最小值；（3）求证：     在直角坐标系中，曲线C1的参数方程为（其中为参数），以坐标原点O为极点，轴的非负半轴为极轴建立极坐标系，曲线C2的极坐标方程为（1）求曲线C1的普通方程和C2的直角坐标方程；（2）若A、B分别为曲线C1，C2上的动点，求当|AB|取最小值时ΔAOB的面积       23.已知恒成立（1）求实数的最大值；（2）若实数的最大值为，正数满足，求的最小值