


人教版七年级上册4.3.2 角的比较与运算授课课件ppt
展开角的比较 角的和差角的平分线
问题:有一天学生张虎和王鹏各带了一把折扇(如图),下面是他们的一段对话:
张:我的折扇大一些,所以我的折扇的角 也大一些.
王:我的折扇长一些,所以我的折扇的角也大一些.
同学们,你们有办法帮他们进行判断吗?
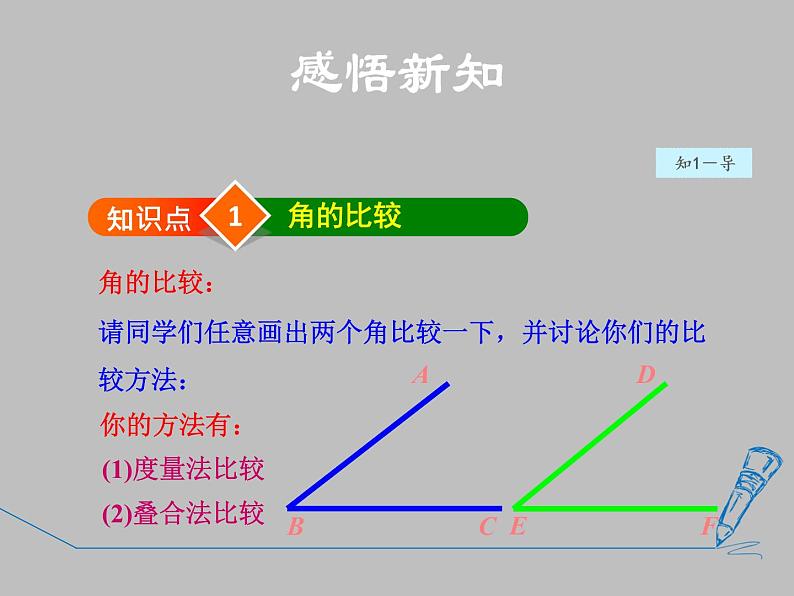
怎样比较∠ABC和∠DEF的大小?
请同学们任意画出两个角比较一下,并讨论你们的比较方法:
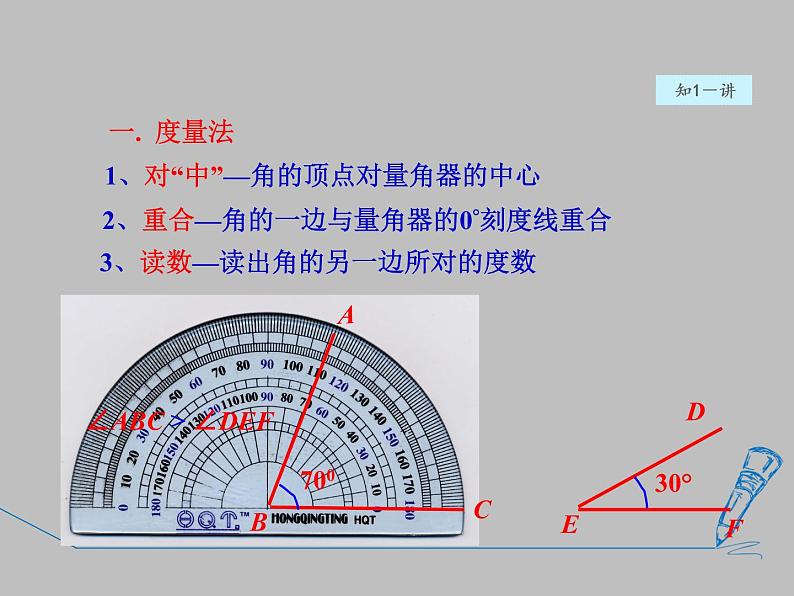
1、对“中”—角的顶点对量角器的中心
3、读数—读出角的另一边所对的度数
2、重合—角的一边与量角器的0°刻度线重合
∠ABC > ∠DEF
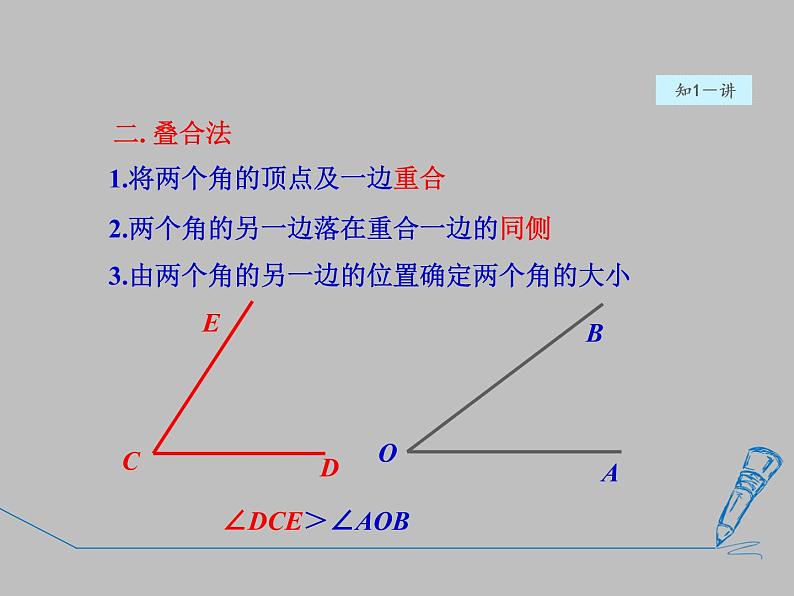
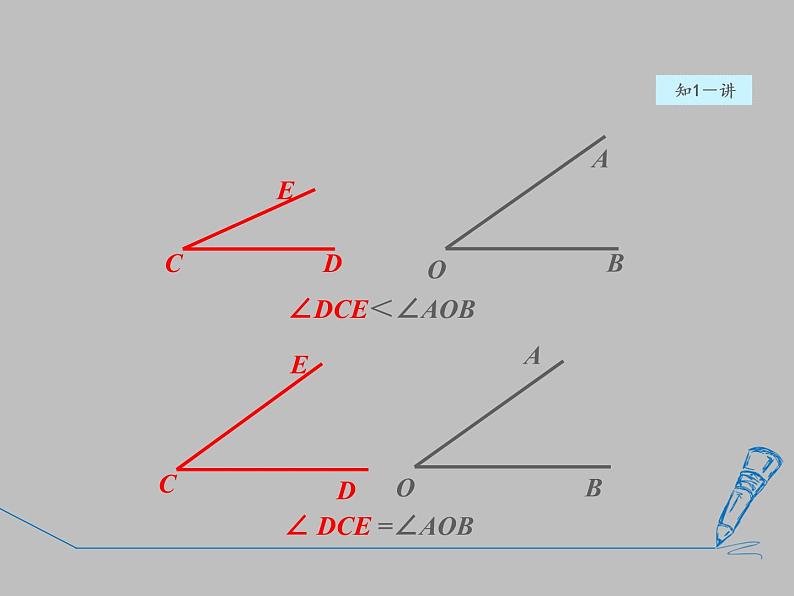
1.将两个角的顶点及一边重合
2.两个角的另一边落在重合一边的同侧
3.由两个角的另一边的位置确定两个角的大小
∠ DCE =∠AOB
例1 根据图,回答下列问题: (1)比较∠FOD与∠FOE的大小; (2)借助三角尺比较∠DOE 与∠DOF 的大小.导引:(1)中两个角有重合边和重合顶点,利用叠合法 比较一目了然,因为OD 边在∠FOE的内部, 所以有∠FOD <∠FOE. (2)∠DOE明显大于 45°,而∠DOF 明显小于 45°,故有∠DOE >∠DOF.
解:(1)∠FOD<∠FOE. (2)用含有45°角的三角尺比较,可得∠DOE> 45°,∠DOF<45°,所以∠DOE>∠DOF.
用叠合法比较角的大小时,一定要将两个角的另一边落在重合边的同侧.两边都不重合,或有一边重合但另一边在重合边的异侧的两角,可通过度量法比较大小.
在∠AOB的内部任取一点C,作射线OC,那么有( )A.∠AOC=∠BOC B.∠AOC>∠BOCC.∠BOC>∠AOB D.∠AOB>∠AOC如图,如果∠AOB=∠COD,那么( ) A.∠1>∠2 B.∠1=∠2C.∠1<∠2 D.以上都不对
思考 如图,图中共有几个角?它们之间有 什么关系? 图中,∠AOC 是∠AOB 与∠BOC 的和,记作∠AOC=∠AOB + ∠BOC. ∠AOB 是∠AOC 与∠BOC 的差,记作∠AOB = ∠AOC -∠BOC. 类似地,∠AOC-∠AOB=____________.
例2 如图, O是直线AB上一点, ∠AOC=53°17′,求 ∠BOC的度数.分析:AB是直线,∠AOB是平角.∠BOC 与∠AOC的 和是∠AOB. 解:由题意可知,∠AOB是平角, ∠AOB= ∠AOC+∠BOC. 所以 ∠BOC =∠AOB-∠AOC =180°-53°17′ =126°43′.
这里的加与减,要将度与度、分与分、秒与秒分别相加、减,分秒相加时逢60要进位,相减时要借1作60. 本题中应借1°,化为60′.
例3 如图,∠AOB=48°,∠1= 32°24′,求∠2的度数.导引:要求∠2的度数,就是要把它转 化为用已知角∠1的关系式来表示.根据图形可 知,∠1+∠2=∠AOB,因此∠2=∠AOB-∠1. 解:因为∠AOB=48°,∠1=32°24′, 所以∠2=48°-32°24′ =47°60′-32°24′=15°36′.
例4 如图,OC是∠AOD的平分线, OE是∠BOD的平分线. (1)如果∠AOB=130°,那么 ∠COE是多少度? (2)在(1)的条件下,如果∠DOC =20°,那么∠BOE是多少度?导引:(1)由已知可知∠DOC= ∠AOD,∠DOE= ∠BOD.由于∠COE=∠DOC+∠DOE,因此, ∠COE= ∠AOD+ ∠BOD= ∠AOB. (2)结合(1)的结论可求出∠DOE的度数,从而求出 ∠BOE的度数.
解:(1)因为OC平分∠AOD, 所以∠DOC= ∠AOD. 因为OE平分∠BOD, 所以∠DOE= ∠BOD. 所以∠COE=∠DOC+∠DOE= (∠AOD+∠BOD) ∠AOB= ×130°=65°. (2)由(1)可知∠COE=65°,因为∠DOC=20°, 所以∠DOE=∠COE-∠DOC=45°. 因为OE平分∠BOD, 所以∠BOE=∠DOE=45°.
(1)利用角平分线进行计算时,要灵活运用角平分 线的几种不同表达方式.(2)在计算角的大小时,常常要用到等量代换,用 已知角代替与它相等的未知角.
如图,∠AOD-∠AOC=( )A.∠AOC B.∠BOC C.∠BOD D.∠COD(中考•滨州)借助一副三角尺,你能画出下面哪个度数的角( )A.65° B.75° C.85° D.95°
(中考•辽宁)如图,已知直线AB,CD相交于点O,OA平分∠EOC,∠EOC=110°,则∠BOD的度数是( )A.25° B.35° C.45° D.55°
如图,在透明纸上画一个角,沿着顶点对折,使角的两边重合.∠AOC被折痕OB分成的两个角有什么关系?
1.定义:一般地,从一个角的顶点出发,把这个角分 成两个相等的角的射线,叫做这个角的平分线.要点精析: (1)角平分线是在角的内部从角的顶点引出的一条射 线,不是直线或线段; (2)角平分线把角分成了两个相等的角.
2.角平分线的几何表示:如图所示, 若OC平分∠AOB,则∠AOC= ∠BOC= ∠AOB;反之,若 ∠AOC=∠BOC,则OC平分∠AOB.3.角的n等分线:类似角的平分线,从角的顶点引出的 射线,将角分成相等的n个角,叫做角的n等分线, 例如角的三等分线、四等分线等.4.易错警示:不能在角平分线的多种几何表达形式之 间灵活转换.
例2 如图,∠1=∠2,∠3=∠4,则 下列结论:①AD平分∠BAF; ②AF平分∠DAC;③AE平分 ∠DAF;④AF平分∠BAC; ⑤AE平分∠BAC中,正确的有( ) A.4个 B.3个 C.2个 D.1个导引:由角的平分线的几何表示可知:当∠1=∠2时, AE平分∠DAF;再由∠3=∠4可得∠1+∠3= ∠2+∠4,即∠BAE=∠CAE,因此AE平分 ∠BAC.
判断一条射线是不是角的平分线,只要看这条射线是否将角分成相等的两个角即可.
点P在∠MAN的内部,现有4个等式;①∠PAM=∠NAP;②∠PAN= ∠MAN;③∠MAP=∠MAN;④∠MAN=∠MAP+∠PAN,其中能表示AP是∠MAN的平分线的有( )A.1个 B.2个C.3个 D.4个
如图所示,若有∠BAD=∠CAD,∠BCE=∠ACE,则下列结论中错误的是( )A.AD是∠BAC的平分线B.CE是∠ACD的平分线C.∠BCE= ∠ACBD.CE是∠ABC的平分线(中考•大连)如图,点O在直线AB上,射线OC平分∠BOD,若∠COB=35°,则∠AOD等于( )A.35° B.70° C.110° D.145°
人教版七年级上册第四章 几何图形初步4.3 角4.3.2 角的比较与运算习题课件ppt: 这是一份人教版七年级上册第四章 几何图形初步4.3 角4.3.2 角的比较与运算习题课件ppt,共23页。PPT课件主要包含了答案显示,平分线,见习题,°或150°等内容,欢迎下载使用。
初中数学人教版七年级上册4.3.2 角的比较与运算教案配套ppt课件: 这是一份初中数学人教版七年级上册4.3.2 角的比较与运算教案配套ppt课件,文件包含432角的比较与运算pptx、432角的比较与运算docx等2份课件配套教学资源,其中PPT共30页, 欢迎下载使用。
人教版七年级上册4.3.2 角的比较与运算图文ppt课件: 这是一份人教版七年级上册4.3.2 角的比较与运算图文ppt课件,共27页。PPT课件主要包含了ABCD,比较线段长短的方法,度量法,叠合法,知识回顾,学习目标,课堂导入,新知探究,跟踪训练,它们的关系等内容,欢迎下载使用。













