2021届湖南省株洲高三一模数学试卷-理科（含答案解析）

湖南省株洲市2021年高三一模数学（理）试题

学校:___________姓名：___________班级：___________考号：___________

一、单选题

1．集合，，则是(      )

A． B． C． D．

2．已知复数为纯虚数，那么实数a的值为(      )

A．－1 B．0 C．1 D．2

3．已知（      ）

A． B． C． D．

4．已知数列的前项和为,,,则 (     )

A． B． C． D．

5．在面积为1的等边三角形ABC内任取一点P，使三角形ABP，ACP，BCP的面积都小于的概率为(        )

A． B． C． D．

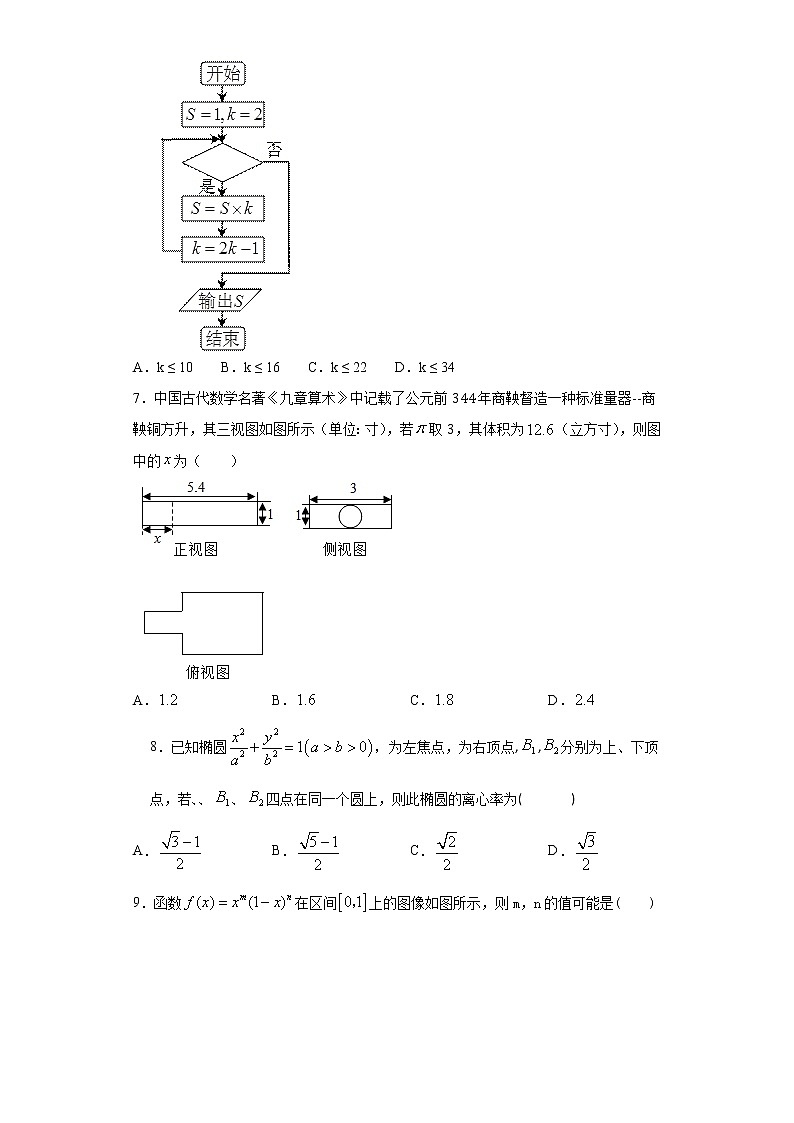
6．如图所示的程序框图表示求算式“” 之值，则判断框内可以填入         (     )

A．    B．    C．    D．

7．中国古代数学名著《九章算术》中记载了公元前344年商鞅督造一种标准量器--商鞅铜方升，其三视图如图所示（单位：寸），若取3，其体积为（立方寸），则图中的为（　　）

A． B． C． D．

8．已知椭圆，为左焦点，为右顶点,,分别为上、下顶点，若、、、四点在同一个圆上，则此椭圆的离心率为(       )

A． B． C． D．

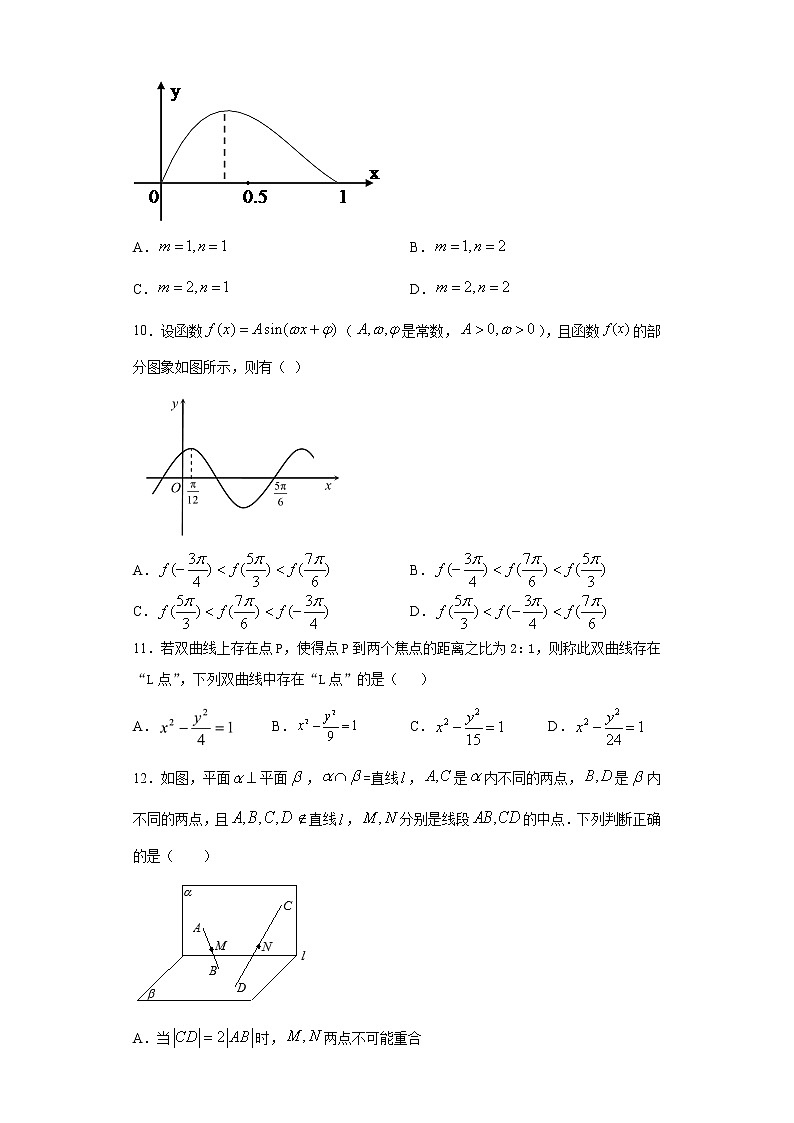
9．函数在区间上的图像如图所示，则m，n的值可能是(    )

A． B．

C． D．

10．设函数（是常数，），且函数的部分图象如图所示，则有（ ）

A． B．

C． D．

11．若双曲线上存在点P，使得点P到两个焦点的距离之比为2：1，则称此双曲线存在“L点”，下列双曲线中存在“L点”的是（   ）

A． B． C． D．

12．如图，平面平面，=直线，是内不同的两点，是内不同的两点，且直线，分别是线段的中点．下列判断正确的是（    ）

A．当时，两点不可能重合

B．两点可能重合，但此时直线与不可能相交

C．当与相交，直线平行于时，直线可以与相交

D．当是异面直线时，直线MN可能与平行

二、填空题

13．在菱形中，，，为的中点，则的值是_______；

14．在的展开式中，x3项的系数为____（用数字作答）

15．某市家庭煤气的使用量和煤气费(元)满足关系

已知某家庭今年前三个月的煤气费如下表：

若四月份该家庭使用了的煤气，则其煤气费为____元.

16．正整数数列满足：， ,将数列中所有值为1的项的项数按从小到大的顺序依次排列，得到数列，， =________（用表示）

三、解答题

17．在梯形中， ，，，．

（Ⅰ）求的长；

（Ⅱ）求梯形的高．

18．如图，四棱锥P—ABCD中，底面ABCD是直角梯形，∠DAB=90°，AD//BC，且BC⊥PB，△PAB是等边三角形，DA=AB=2，BC=AD，E是线段AB的中点.

（I）求证：PE⊥CD；

（II）求PC与平面PDE所成角的正弦值.

19．小型风力发电项目投资较少，开发前景广阔.受风力自然资源影响，项目投资存在一定风险.根据测算，IEC（国际电工委员会）风能风区的分类标准如下：

某公司计划用不超过100万元的资金投资于A、B两个小型风能发电项目.调研结果是：未来一年内，位于一类风区的A项目获利%的可能性为0.6，亏损%的可能性为0.4；

B项目位于二类风区，获利35%的可能性为0.6，亏损10%的可能性是0.2，不赔不赚的可能性是0.2.

假设投资A项目的资金为（）万元，投资B项目资金为（）万元，且公司要求对A项目的投资不得低于B项目.

（Ⅰ）记投资A，B项目的利润分别为和，试写出随机变量与的分布列和期望，;

（Ⅱ）根据以上的条件和市场调研，试估计一年后两个项目的平均利润之和 的最大值，并据此给出公司分配投资金额建议.

20．已知，坐标平面上一点P满足：的周长为6，记点P的轨迹为.抛物线以为焦点，顶点为坐标原点O.

（Ⅰ）求，的方程；

（Ⅱ）若过的直线与抛物线交于两点,问在上且在直线外是否存在一点,使直线的斜率依次成等差数列,若存在,请求出点的坐标,若不存在,请说明理由.

21．已知函数，实数是常数.

（Ⅰ)若=2，函数图像上是否存在两条互相垂直的切线，并说明理由.

（Ⅱ）若在上有零点，求实数的取值范围.

22．选修44：坐标系与参数方程

在平面直角坐标系中，圆C的参数方程为，（t为参数），在以原点O为极点，x轴的非负半轴为极轴建立的极坐标系中，直线的极坐标方程为，A，B两点的极坐标分别为.

(Ⅰ)求圆C的普通方程和直线的直角坐标方程；

(Ⅱ)点P是圆C上任一点，求△PAB面积的最大值.

23．选修45：不等式选讲

已知函数.

(Ⅰ)解不等式：；

(Ⅱ)若使得成立，求实数的取值范围.

参考答案

1．A

【解析】

因为，所以，应选答案A。

2．B

【解析】

因为，所以，应选答案B．

3．C

【解析】

因为，所以，，应选答案C。

4．C

【解析】

因为，所以，故数列是首项为1，公比为3的等比数列，则，应选答案C。

5．D

【解析】

如图，设分别是正三角形的三边上的中点，当点时同时满足ABP，ACP，BCP的面积都小于，因为，所以所求事件的概率是，应选答案D。

6．C

【解析】

试题分析：由程序图可得

，

当k<34时，输出，选C.

考点：程序结构为当型循环结构.

7．B

【解析】

由三视图知，商鞅铜方升由一圆柱和一长方体组合而成，由题意得：，，故选B.

8．B

【解析】

由题设圆的半径，则，即，解之得，应选答案B。

9．B

【解析】

当时，函数，应在处取最大值，故与题设中提供的图像不符，排除答案A；当时，函数，则，应在处取最大值，故与题设中提供的图像不符，排除答案C；当时，函数，则，应在处取最大值，故与题设中提供的图像不符，排除答案D，应选答案B。

点睛：解答本题的方法是答案筛选排除法，求解时综合运用所学知识，对题设中所给的四个答案进行分析和判断，从而排除错误的答案，选出正确的答案而获解。

10．D

【解析】

借助题设中的图像可得，所以，则，所以，即，则，所以，容易算得，，应选答案D．

点睛：解答本题的思路是先借助题设中提供的图像数据信息，求出其中的参数和，进而确定函数的解析式，然后再分别计算，，，从而比较出其大小关系使得问题获解．

11．A

【解析】

因，不妨设，则由双曲线的定义可得，即，与双曲线方程联立可得，其判别式，故存在“点”，应选答案A．

12．B

【解析】

由于直线的两个端点都可以动，所以两点可能重合，此时两条直线共面，由于两条线段互相平分，所以四边形是平行四边形，因此，则，所以由线面平行的判定定理可得，又因，所以由线面平行的性质定理可得，故应排除答案A ，C ，D，应选答案B。

点睛：解答本题的关键是充分借助题设的中的动点、中点等信息，运用分析推理判断等思维方式和平面几何中的特殊四边形（平行四边形的判定和性质为依托）进行分析推断从而使得问题获解。

13．1

【解析】

如图所示：

在菱形中，，
∴
故答案为1

14．20;       

【解析】

因展开式的通项公式为，令，故其系数是，应填答案。

15．11.5;

【解析】

由题设可得，且，故，则，应填答案。

点睛：解答本题的难点在于不知道函数的解析式的对应关系，需要进行分析和推断，然后运用题设条件建立方程组从而求出函数解析式中的参数，确定函数的解析式，求出了问题燃气的燃气费中而获解。

16．

【解析】

因为，所以当，由题设可知或，而通过计算不难看出其规律：要么被3整除余1，即的形式，要么是的形式，故，，应填答案。

点睛：解答本题的关键是充分挖掘题设中的题设信息，通过数列递推式建立方程计算出满足题设条件的项的项数，并观察其数式的规律，运用归纳推理的思维方式进行抽象概括，从而使得问题获解。

17．（1）（2）梯形的高为

【解析】

【试题分析】（1）先求，再运用正弦定理分析求解；（2）运用解直角三角形的知识分析求解：

解：（Ⅰ）在中，因为，

所以

由正弦定理得：

（Ⅱ）在中，由余弦定理解得

过点D作在于E，

在直角中，．

即梯形的高为

18．（1）见解析（2）PC与平面PDE所成角的正弦值为

【解析】

【试题分析】（1）先借助题设条件证明线面垂直，再运用线面垂直的性质定理分析推证；（2）建立空间直角坐标系，运用向量的坐标形式的运算及向量的数量积公式分析求解：

解：（I）证明：因为BC⊥AB,BC⊥PB,

所以BC⊥侧面PAB，

PE平面PAB，所以BC⊥PE.        

又因为△PAB是等边三角形，E是线段AB的中点，

所以PE⊥AB.

因为AD∩AB=A，

所以PE⊥平面ABCD.   

而CD平面ABCD，所以PE⊥CD.   

（II）以E为原点，建立如图所示的空间直角坐标系E—xyz.

则E（0,0,0），C（1，-1,0），D（2,1,0），P（0,0，）

有,,

设=(x,y,z)为平面PDE的法向量.

由

令x=1可得

设PC与平面PDE所成的角为

所以PC与平面PDE所成角的正弦值为

19．（1）见解析（2）最大为17.5万元，建议给两公司各投资50万.

【解析】

【试题分析】（1）运用随机变量的概率分布及数学期望计算公式进行分析求解；（2）依据题设条件运用线性规划的知识分析求解：

解：（1）A项目投资利润的分布列

B项目投资利润的分布列

（2）

而

如图所示

由图可知，当 ，公司获得获利最大，最大为17.5万元.

建议给两公司各投资50万.

20．（1）的方程为： ，的方程为：.

（2）见解析

【解析】

【试题分析】（1）依据题设条件及椭圆的定义求出，进行求解；（2）依据题设条件建立直线的方程然后与椭圆方程联立，运用交点坐标之间的关系分析求解：

解：（Ⅰ）依题意可知，的周长为，由于，故，由于，故点P的轨迹为为以为焦点的椭圆的一部分，且，故，故的方程为： ，的方程为：.

（Ⅱ）设，设直线的方程为：，

由，，

故，

又，

故，

，

故，

因为直线不经过点M，故，故或，

当时，上除点外，均符合题意；

当时,则当时，椭圆上存在两点和都符合条件.

点睛：椭圆是高中数学中重要的圆锥曲线代表，也是高考重点考查的重要知识点和考点。这类问题的设置旨在考查椭圆的标准方程和几何性质，以及运用方程函数等代数思想和方法研究几何的性质。解答本题的关键是运用椭圆的定义先求出椭圆的标准方程和抛物线的标准方程，从而使得问题获解；求解第二问时，先依据题设条件建立直线的方程，然后与椭圆方程联立，借助方程的根即交点坐标之间的关系进行分析求解，从而使得问题获解。

21．（1）函数图像上不存在两条互相垂直的直线（2）的取值范围是.

【解析】

【试题分析】（1）借助导数的几何意义分别求出其斜率，依据题设建立不等式进行分析推证；（2）先将问题进行等价转化与化归为函数在区间上的最小值小于等于0，再借助导数知识进行分析探求：

 (Ⅰ)，，

则

所以，对于任意，均有，

故函数图像上不存在两条互相垂直的直线

(Ⅱ)解：因为在上有零点，

所以在区间上的最小值小于等于0. 

因为, 令,得.  

（1）当时，即时，

因为对成立，所以在上单调递增，

此时在上的最小值为

所以，

解得，所以此种情形不成立，

（2）当，即时，

①若, 则对成立，所以在上单调递增，

此时在上的最小值为所以，

解得，所以

②若，

若，则对成立，对成立.

则在上单调递减，在上单调递增，此时在上的最小值为所以有，解得，

若时，注意到,而，

      此时结论成立.

综上，的取值范围是.

点睛：本题以含参数的函数解析式为背景，精心设置了两个问题，旨在考查导数知识在研究函数的单调性、极值（最值）等方面的综合运用。求解本题的第一问时，充分借助导数的几何意义，建立不等式进行分析推证从而获解；第二问的求解则先将问题进行等价转化与化归，再构造方程进行分析探求参数的取值范围从而使得问题获解。

22．(Ⅰ),; (Ⅱ).

【解析】

试题分析：(Ⅰ) 利用 将圆C的参数方程化为普通方程，由 ，将直线 的极坐标方程化为直角坐标方程；(Ⅱ)写出点P的坐标 ，由点到直线的距离求出P点到直线的距离，求出最大值，从而得到 面积的最大值.

试题解析：(Ⅰ)由得消去参数t，得，

所以圆C的普通方程为．

由，得，

即，化成直角坐标系为，所以直线l的直角坐标方程为 

(Ⅱ)化为直角坐标为在直线l上，并且，…7分

设P点的坐标为，

则P点到直线l的距离为 ，

，

所以面积的最大值是

23．（1）．（2）

【解析】

【试题分析】（1）借助绝对值的定义运用分类整合思想分别解不等式进行分析求解；（2）依据题设条件，运用绝对值三角不等式建立不等式分析求解：

（1）解：，即，

①当时，不等式为，即，

是不等式的解；

②当时，不等式为，即恒成立，

∴是不等式的解；

③当时，不等式为，即，

是不等式的解．

综上所述，不等式的解集为（1）．

（2）

，

的最小值为

又使得成立，

得