浙教版3.4 简单几何体的表面展开图优秀课件ppt

这是一份浙教版3.4 简单几何体的表面展开图优秀课件ppt，文件包含34简单几何体的表面展开图2课件ppt、34简单几何体的表面展开图2教案doc、34简单几何体的表面展开图2学案doc等3份课件配套教学资源，其中PPT共24页， 欢迎下载使用。
那么怎样得到圆柱、圆锥等简单旋转体的表面展开图呢？
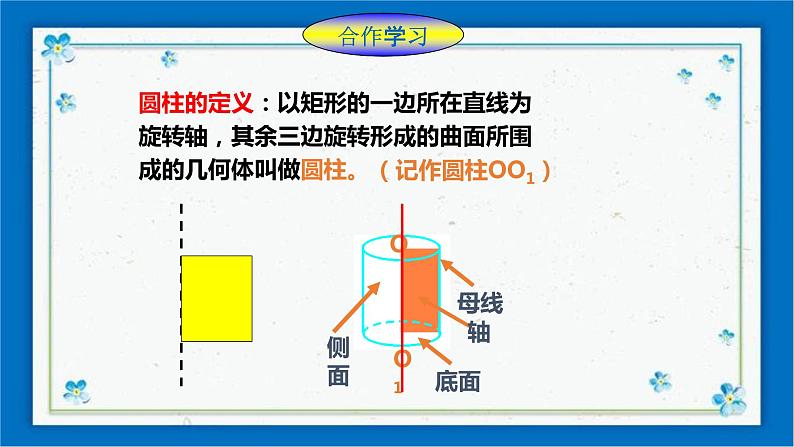
圆柱的定义：以矩形的一边所在直线为旋转轴，其余三边旋转形成的曲面所围成的几何体叫做圆柱。
由此可得圆柱的有关概念： 如图，圆柱可以看作矩形ABCD绕边BC所在直线___________，其余各边所成的面围成的几何体。AB,CD旋转所成的面就是圆柱的两个底面，是两个半径相同的圆。AD旋转所成的面就是圆柱的侧面。AD不论转到哪个位置，都是圆柱的母线．
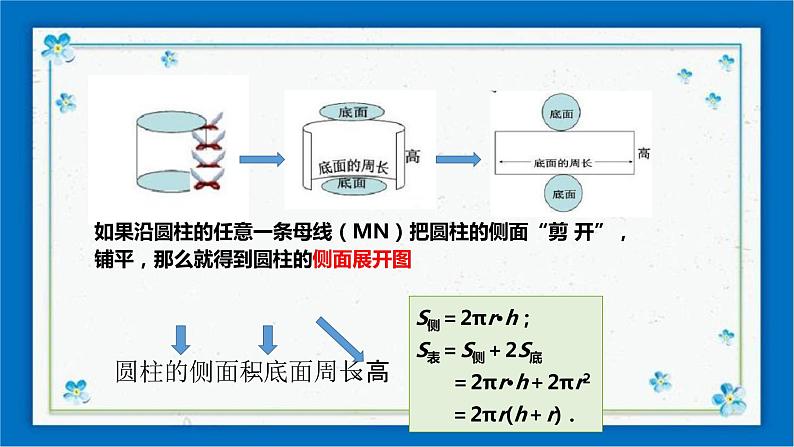
如果沿圆柱的任意一条母线（MN）把圆柱的侧面“剪 开”，铺平，那么就得到圆柱的侧面展开图
S侧＝2πr·h；S表＝S侧＋2S底 ＝2πr·h＋2πr2 ＝2πr(h＋r)．
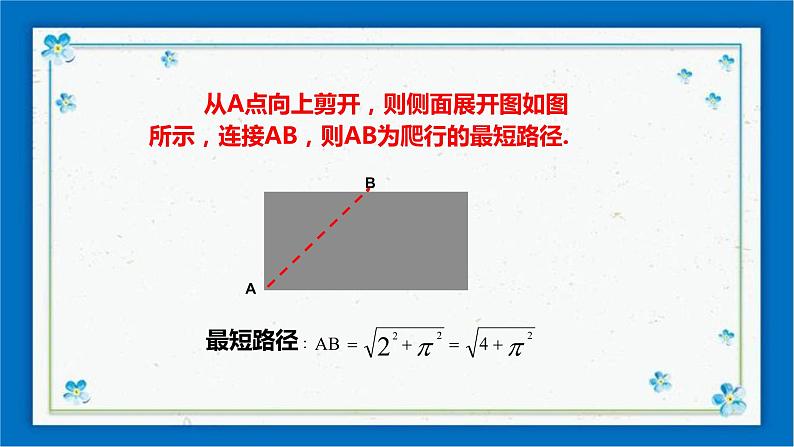
在底面半径为1、高为2的圆柱体的左下角A处有一只蚂蚁，欲从圆柱体的侧面爬行去吃右上角B处的食物，问怎样爬行路径最短，最短路径是多少？
圆柱的表面展开图：将圆柱的侧面沿它的一条母线剪开，会得到圆柱的侧面展开图为矩形，其中一边长等于圆柱的高，另一边长是底面圆的周长．所以圆柱的侧面积等于 底面圆的周长乘以圆柱的高．如图，若圆柱的底面半径为r，高为h，则S侧＝2πr·h；S表＝S侧＋2S底 ＝2πr·h＋2πr2＝2πr(h＋r)．
从A点向上剪开，则侧面展开图如图所示，连接AB，则AB为爬行的最短路径.
如图,一油桶高2米,底面直径1 米,一只壁虎由A到B吃一害虫,需要爬行的最短路程是多少?
例1 如图为一个圆柱的三视图.以相同的比例画出 它的表面展 开图，并计算它的侧面积和全面积(果保留π).
S侧=2πrl=2×π×0.9×2.4=4.32π (cm²)；S=2πr²+2πrl=2π×0.9²+2π×0.9×2.4=5.94π (cm²).答：这个圆柱的侧面积为4.32πcm²，全面积为5.94πcm².
解:所求圆柱的表面展开,图如图
圆柱的侧面积与全面积侧面展开图：长为圆柱底面圆周长，宽为圆柱母线长的长方形．侧面积＝展开图长方形的面积；全面积＝侧面积＋底面积．
1.如图，已知MN是圆柱底面的直径，NP是圆柱的高，在圆柱的侧面上，过点M，P嵌有一条路径最短的金属丝，现将圆柱侧面沿NP剪开，所得的侧面展开图是(　 　)
2.一个几何体的三种视图如图3－4－28所示，这个几何体的表面积是_________(结果保留 π)．
3.请阅读下列材料：问题：如图，圆柱的底面半径为1 dm，BC是底面直径，圆柱高AB为5 dm，求一只蚂蚁从点A出发沿圆柱表面爬行到点C的最短路线，小明设计了两条路线：路线1：高线AB＋底面直径BC，如图①所示．路线2：侧面展开图中的线段AC，如图②所示．
(1)设路线1的长度为l1，则l12＝49.设路线2的长度为l2，则l22＝25＋π2.所以选择路线______(填“1”或“2”)较短．(2)小明把条件改成：“圆柱的底面半径为5 dm，高AB为1 dm”继续按前面的路线进行计算．此时，路线1，l12＝121.路线2，l22＝1＋25 π2.所以选择路线______(填“1”或“2”)较短．(3)请你帮小明继续研究：当圆柱的底面半径为2 dm，高为h dm时，应如何选择上面的两条路线才能使蚂蚁从点A出发沿圆柱表面爬行到点C的路线最短(结果保留π)．
解：(1)∵49＞25＋π2，∴选择路线2较短；(2)∵l12＝121，l22＝1＋25 π2，∵l12－l22