2019-2020学年湖南省长沙市开福区青竹湖湘一外国语学校七年级（上）期末数学试卷

这是一份2019-2020学年湖南省长沙市开福区青竹湖湘一外国语学校七年级（上）期末数学试卷，共20页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
1．（3分）29的倒数是
A．29B．C．D．
2．（3分）中国倡导的“一带一路”建设将促进我国与世界各国的互利合作，根据规划“一带一路”地区覆盖总人口44亿，这个数用科学记数法表示为
A．B．C．D．
3．（3分）如图，能用、、三种方法表示同一个角的是
A．B．
C．D．
4．（3分）若，则的值为
A．B．4C．0D．
5．（3分）单项式的系数和次数分别为
A．，2B．，3C．3，3D．，1
6．（3分）某商品的标价为200元，8折销售仍赚40元，则商品进价为 元．
A．140B．120C．160D．100
7．（3分）已知多项式的值是，则多项式的值是
A．B．C．1D．7
8．（3分）如图，点在的延长线上，下列条件中能判断
A．B．C．D．
9．（3分）有下列命题，其中假命题有
①对顶角相等：
②垂直于同一条直线的两直线平行；
③平行于同一条直线的两直线平行；
④内错角相等．
A．①②B．①③C．②④D．③④
10．（3分）根据等式的性质，下列变形正确的是
A．如果，那么B．如果，那么
C．如果，那么D．如果，那么
11．（3分）如图，在、两座工厂之间要修建一条笔直的公路，从地测得地的走向是南偏东，现、两地要同时开工，若干天后公路准确对接，则地所修公路的走向应该是
A．北偏西B．南偏东C．西偏北D．北偏西
12．（3分）乐乐观察“抖空竹”时发现，可以将某一时刻的情形抽象成数学问题：如图，已知，，，则的度数是
A．B．C．D．
二、填空题（本题共6个小题，每小题3分，共18分）
13．（3分）长沙某天白天气温最高为，夜间最低为，则长沙当天的最大温差为 ．
14．（3分）方程，处被墨水盖住了，已知该方程的解是，那么处的数字是 ．
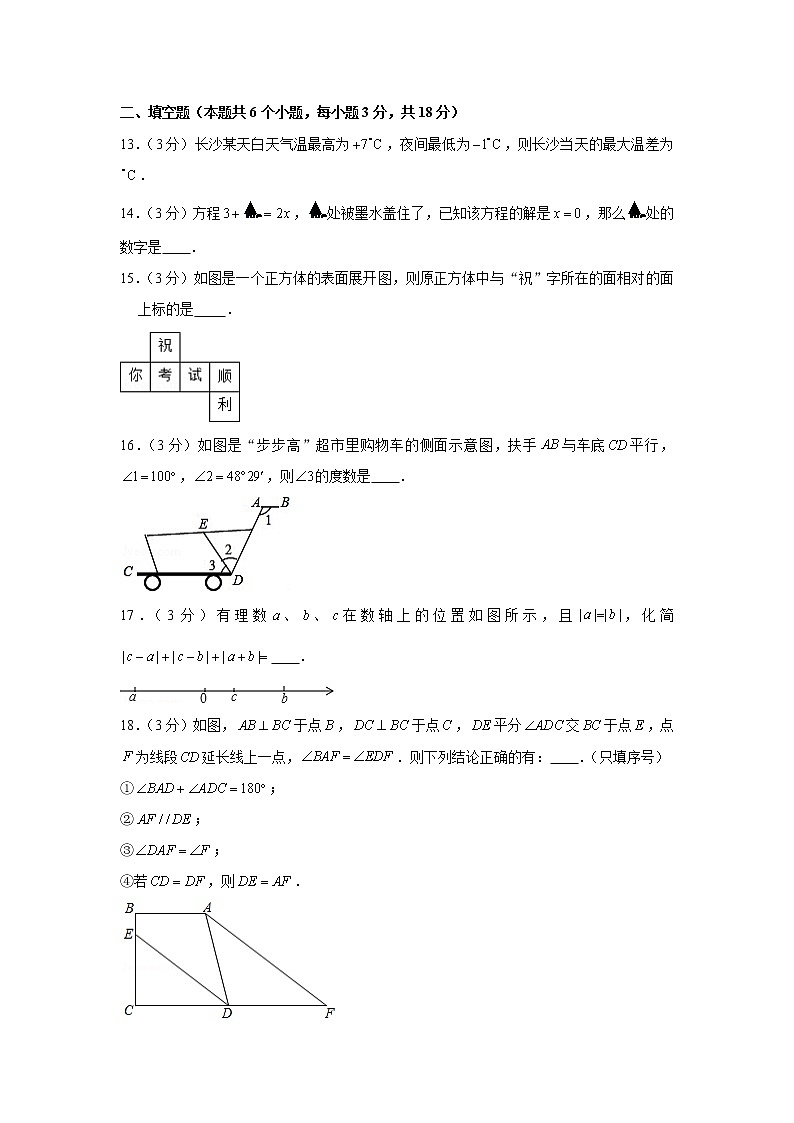
15．（3分）如图是一个正方体的表面展开图，则原正方体中与“祝”字所在的面相对的面上标的是 ．
16．（3分）如图是“步步高”超市里购物车的侧面示意图，扶手与车底平行，，，则的度数是 ．
17．（3分）有理数、、在数轴上的位置如图所示，且，化简 ．
18．（3分）如图，于点，于点，平分交于点，点为线段延长线上一点，．则下列结论正确的有： ．（只填序号）
①；
②；
③；
④若，则．
三、解答题（本题共8小题，共66分）
19．（6分）（1）计算：
（2）解方程：
20．（6分）先化简，再求值：，其中，．
21．（8分）如图，已知，，垂足分别为、，，试说明：．请补充说明过程，并在括号内填上相应的理由．
解：，（已知）
，
，
．
又（已知），
，
，
．
22．（8分）如图为直线上一点，，平分，．
（1）求的度数；
（2）试判断是否平分，并说明理由．
23．（9分）青竹湖湘一外国语学校初2019级全体学生从学校统一乘车去市科技馆参观学习，然后又统一乘车原路返回，需租用客车若干辆．现有甲、乙两种座位数相同的客车可以租用，甲种客车每辆的租金为300元，另按实际行程每千米加收8元；乙种客车每辆按每千米14元收费．
（1）当行程为多少千米时，租用两种客车的费用相同？
（2）青竹湖湘一外国语学校距市科技馆约30公里，如果你是年级组杨组长，为节省费用，你会选择哪种客车？
24．（9分）（1）如图1，在直线上，点在、两点之间，点为线段的中点，点为线段的中点，若，且使关于的方程无解．
①求线段的长；
②线段的长与点在线段上的位置有关吗？请说明理由；
（2）如图2，点为线段的中点，点在线段的延长线上，试说明的值不变．
25．我们把解相同的两个方程称为同解方程．例如：方程：与方程的解都为，所以它们为同解方程．
（1）若方程与关于的方程是同解方程，求的值；
（2）若关于的方程和是同解方程，求的值；
（3）若关于的方程和是同解方程，求的值．
26．将一副直角三角板按图1方式摆放（即与重合、与共线）．
（1）如图2，当绕点旋转至时，求的度数；
（2）若绕点以每秒的速度顺时针旋转，回到起始位置停止，设旋转时间为，当为何值时，与始终不共线）；
（3）若绕点以每秒的速度顺时针旋转的同时，也绕点以每秒的速度顺时针旋转，当回到起始位置时全都停止旋转．设旋转时间为，在运动过程中，当为何值时，的边所在直线恰好平分？试直接写出值．
2019-2020学年湖南省长沙市开福区青竹湖湘一外国语学校七年级（上）期末数学试卷
参考答案与试题解析
一、选择题（本大题共12个小题，每小题3分，共36分）
1．（3分）29的倒数是
A．29B．C．D．
【解答】解：29的倒数是，
故选：．
2．（3分）中国倡导的“一带一路”建设将促进我国与世界各国的互利合作，根据规划“一带一路”地区覆盖总人口44亿，这个数用科学记数法表示为
A．B．C．D．
【解答】解：44亿．
故选：．
3．（3分）如图，能用、、三种方法表示同一个角的是
A．B．
C．D．
【解答】解：、、、三种方法表示的是同一个角，故此选项正确；
、、、三种方法表示的不一定是同一个角，故此选项错误；
、、、三种方法表示的不一定是同一个角，故此选项错误；
、、、三种方法表示的不一定是同一个角，故此选项错误；
故选：．
4．（3分）若，则的值为
A．B．4C．0D．
【解答】解：根据题意得，，
解得，，
则．
故选：．
5．（3分）单项式的系数和次数分别为
A．，2B．，3C．3，3D．，1
【解答】解：单项式的系数和次数分别为：，3．
故选：．
6．（3分）某商品的标价为200元，8折销售仍赚40元，则商品进价为 元．
A．140B．120C．160D．100
【解答】解：设商品的进价为每件元，售价为每件元，由题意，得
，
解得：．
故选：．
7．（3分）已知多项式的值是，则多项式的值是
A．B．C．1D．7
【解答】解：由题意得，，
则，
，
故选：．
8．（3分）如图，点在的延长线上，下列条件中能判断
A．B．C．D．
【解答】解：、错误，若，则；
、错误，若，则；
、错误，若，则；
、正确，若，则．
故选：．
9．（3分）有下列命题，其中假命题有
①对顶角相等：
②垂直于同一条直线的两直线平行；
③平行于同一条直线的两直线平行；
④内错角相等．
A．①②B．①③C．②④D．③④
【解答】解：①对顶角相等，是真命题，不合题意：
②垂直于同一条直线的两直线平行，缺少在同一平面内，故原命题是假命题，符合题意；
③平行于同一条直线的两直线平行，故原命题是真命题，不符合题意；
④内错角相等，缺少两直线平行，故原命题是假命题，符合题意．
故选：．
10．（3分）根据等式的性质，下列变形正确的是
A．如果，那么B．如果，那么
C．如果，那么D．如果，那么
【解答】解：、如果，那么，，故此选项错误；
、如果，那么，故此选项错误；
、如果，那么，正确；
、如果，那么，故此选项错误；
故选：．
11．（3分）如图，在、两座工厂之间要修建一条笔直的公路，从地测得地的走向是南偏东，现、两地要同时开工，若干天后公路准确对接，则地所修公路的走向应该是
A．北偏西B．南偏东C．西偏北D．北偏西
【解答】解：北偏西．
故选：．
12．（3分）乐乐观察“抖空竹”时发现，可以将某一时刻的情形抽象成数学问题：如图，已知，，，则的度数是
A．B．C．D．
【解答】解：如图，延长交于，
，，
，
又，
．
故选：．
二、填空题（本题共6个小题，每小题3分，共18分）
13．（3分）长沙某天白天气温最高为，夜间最低为，则长沙当天的最大温差为 8 ．
【解答】解：长沙当天的最大温差为：．
故答案为：8
14．（3分）方程，处被墨水盖住了，已知该方程的解是，那么处的数字是 ．
【解答】解：把代入方程，得▲，
解得：▲．
故答案为：．
15．（3分）如图是一个正方体的表面展开图，则原正方体中与“祝”字所在的面相对的面上标的是 利 ．
【解答】解：正方体的表面展开图，相对的面之间一定相隔一个正方形，
“祝”与“利”是相对面，
“你”与“试”是相对面，
“考”与“顺”是相对面．
故答案为：利．
16．（3分）如图是“步步高”超市里购物车的侧面示意图，扶手与车底平行，，，则的度数是 ．
【解答】解：，，，
，
．
故答案为：．
17．（3分）有理数、、在数轴上的位置如图所示，且，化简 或 ．
【解答】解：由数轴可得：，且
，
，
当时，原式；
当时，原式；
综上，或，
故答案为：或．
18．（3分）如图，于点，于点，平分交于点，点为线段延长线上一点，．则下列结论正确的有： ①②③ ．（只填序号）
①；
②；
③；
④若，则．
【解答】解：于点，于点，
，
①，正确，
，
，
，
，
②，正确；
，
平分交于点，
，
，
，
③，正确；
，无法得出，故④错误；
故答案为：①②③
三、解答题（本题共8小题，共66分）
19．（6分）（1）计算：
（2）解方程：
【解答】解：（1）原式
．
（2）
，
，
，
，
，
20．（6分）先化简，再求值：，其中，．
【解答】解：
，
当，时，原式．
21．（8分）如图，已知，，垂足分别为、，，试说明：．请补充说明过程，并在括号内填上相应的理由．
解：，（已知）
垂直的定义 ，
，
．
又（已知），
，
，
．
【解答】解：，（已知）
（垂直的定义），
（同位角相等两直线平行），
（两直线平行同旁内角互补），
又（已知），
（同角的补角相等），
（内错角相等两直线平行），
（两直线平行同位角相等）．
故答案为：垂直的定义，同位角相等两直线平行，，两直线平行同旁内角互补，同角的补角相等，，内错角相等两直线平行，两直线平行同位角相等．
22．（8分）如图为直线上一点，，平分，．
（1）求的度数；
（2）试判断是否平分，并说明理由．
【解答】解：（1）因为，平分，
所以，，
所以；
（2）平分．理由如下：
因为，，
所以．
又因为，
所以，
所以平分．
23．（9分）青竹湖湘一外国语学校初2019级全体学生从学校统一乘车去市科技馆参观学习，然后又统一乘车原路返回，需租用客车若干辆．现有甲、乙两种座位数相同的客车可以租用，甲种客车每辆的租金为300元，另按实际行程每千米加收8元；乙种客车每辆按每千米14元收费．
（1）当行程为多少千米时，租用两种客车的费用相同？
（2）青竹湖湘一外国语学校距市科技馆约30公里，如果你是年级组杨组长，为节省费用，你会选择哪种客车？
【解答】解：（1）设当行程为千米时，租用两种客车的费用相同，依题意有
，
解得．
故当行程为50千米时，租用两种客车的费用相同；
（2）（元，
（元，
，
为节省费用，会选择甲种客车．
24．（9分）（1）如图1，在直线上，点在、两点之间，点为线段的中点，点为线段的中点，若，且使关于的方程无解．
①求线段的长；
②线段的长与点在线段上的位置有关吗？请说明理由；
（2）如图2，点为线段的中点，点在线段的延长线上，试说明的值不变．
【解答】解：（1）①方程，
关于的方程无解，
，即，
线段的长为4；
②如图1，点为线段的中点，点为线段的中点，，
，，
；
线段的长与点在线段上的位置无关；
（2）如图2，点为线段的中点，
，
，
，
的值不变．
25．我们把解相同的两个方程称为同解方程．例如：方程：与方程的解都为，所以它们为同解方程．
（1）若方程与关于的方程是同解方程，求的值；
（2）若关于的方程和是同解方程，求的值；
（3）若关于的方程和是同解方程，求的值．
【解答】解：（1）方程与关于的方程是同解方程，
，解得，
把代入方程，解得，
所以的值为11；
（2）方程和是同解方程，
解得，，
解得，，
，
解得；
所以的值为；
（3）方程和是同解方程，
即，
，
，
，
即，
．
所以的值为6．
26．将一副直角三角板按图1方式摆放（即与重合、与共线）．
（1）如图2，当绕点旋转至时，求的度数；
（2）若绕点以每秒的速度顺时针旋转，回到起始位置停止，设旋转时间为，当为何值时，与始终不共线）；
（3）若绕点以每秒的速度顺时针旋转的同时，也绕点以每秒的速度顺时针旋转，当回到起始位置时全都停止旋转．设旋转时间为，在运动过程中，当为何值时，的边所在直线恰好平分？试直接写出值．
【解答】解：（1），
，
；
（2）如图3，若与在点两侧，延长交于点，
，
，
，
，
，
；
如图4，若与在点同侧，设与交于点，
，
，
，
，
，
，
综上所述：当为或时，；
（3）若所在直线恰好平分，
，或，
解得：或，
若所在直线恰好平分，
，或，
解得：，或（不合题意舍去）
综上所述：或或时，的边所在直线恰好平分．
声明：试题解析著作权属菁优网所有，未经书面同意，不得复制发布
日期：2021/12/2 14:28:29；用户：初中数学3；邮箱：jse034@xyh.cm；学号：39024124