2019-2020学年河南省商丘市永城市八年级（上）期末数学试卷

2019-2020学年河南省商丘市永城市八年级（上）期末数学试卷

一、选择题（每小题3分，共30分）在每个小题列出的四个选项中，只有一个是正确的，请把答题卡上对应题目所选的选项涂黑.

1．（3分）如图，已知，则一定是的　　

A．角平分线 B．高线 C．中线 D．无法确定

2．（3分）中国科学院微电子研究所微电子设备与集成技术领域的专家殷华湘说，他的团队已经研发出3纳米米纳米）晶体管．将3纳米换算成米用科学记数法表示为　　

A．米 B．米 C．米 D．米

3．（3分）为你点赞，你是最棒的！下列四种表情图片都可以用来为你点赞！其中是轴对称图形的是　　

A． B． C． D．

4．（3分）在平面直角坐标系中，点与点关于轴对称，则在　　

A．第一象限 B．第二象限 C．第三象限 D．第四象限

5．（3分）下列计算中，正确的是　　

A． B． C． D．

6．（3分）如图，在中，，于点，，，则的度数为　　

A． B． C． D．

7．（3分）如图，在中，，是的中点，是上任意一点，连接、并延长分别交、于点、，则图中的全等三角形共有　　

A．7对 B．6对 C．5对 D．4对

8．（3分）在中，为最大角，，，，则的取值范围是　　

A． B． C． D．

9．（3分）三个等边三角形的摆放位置如图所示，若，则的度数为　　

A． B． C． D．

10．（3分）如图，在中，，，点、分别在边、上，，点是边上一动点，当的值最小时，，则为　　

A．30 B．29 C．28 D．27

二、填空题（每小题3分，共15分）

11．（3分）若分式的值为0，则的值为　　．

12．（3分）因式分解：　　．

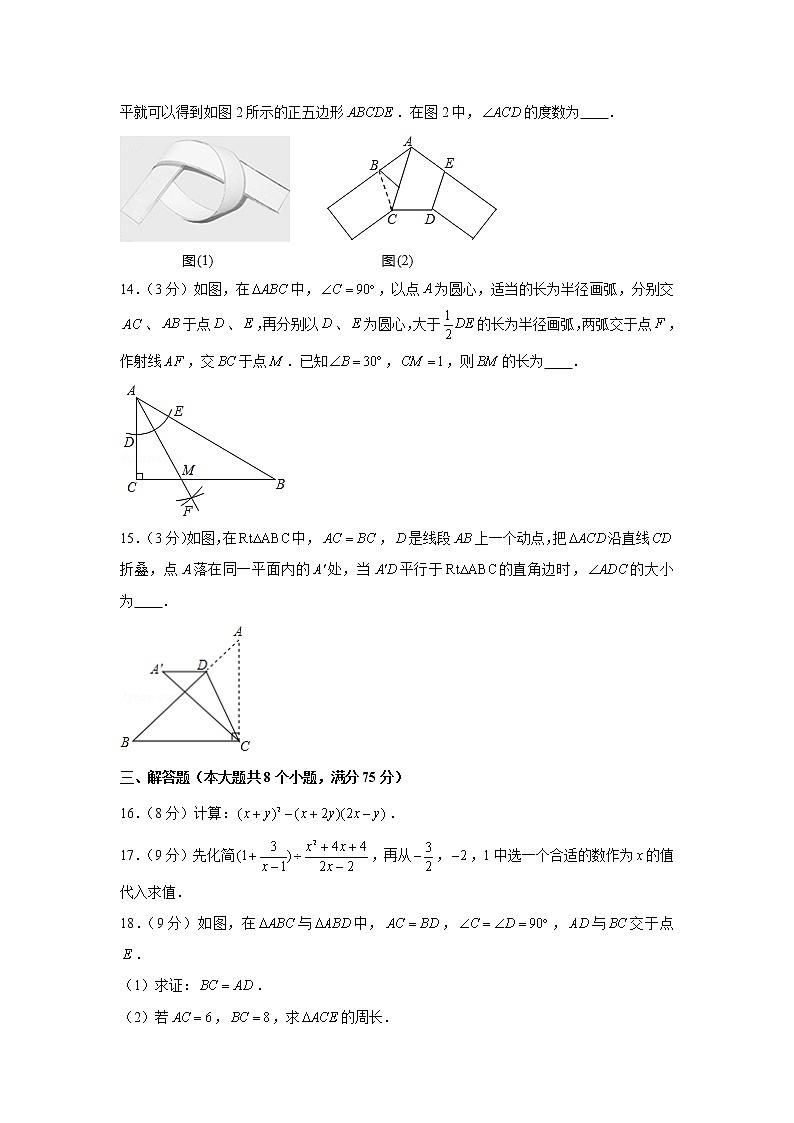
13．（3分）如图，用一条宽度相等的足够长的纸条打一个结（如图，然后轻轻拉紧、压平就可以得到如图2所示的正五边形．在图2中，的度数为　　．

14．（3分）如图，在中，，以点为圆心，适当的长为半径画弧，分别交、于点、，再分别以、为圆心，大于的长为半径画弧，两弧交于点，作射线，交于点．已知，，则的长为　　．

15．（3分）如图，在中，，是线段上一个动点，把沿直线折叠，点落在同一平面内的处，当平行于的直角边时，的大小为　　．

三、解答题（本大题共8个小题，满分75分）

16．（8分）计算：．

17．（9分）先化简，再从，，1中选一个合适的数作为的值代入求值．

18．（9分）如图，在与中，，，与交于点．

（1）求证：．

（2）若，，求的周长．

19．（9分）如图，在四边形中，，的平分线交的延长线于点，是的中点，连接并延长交于点．

（1）求证：平分．

（2）若，，求的度数．

20．（9分）如图，在中，，，，．

（1）求证：．

（2）猜想：与之间存在怎样的数量关系？请说明理由．

21．（10分）现有一段360米长的河堤的整治任务，打算请，两个工程队来完成，经过调查发现，工程队每天比工程队每天多整治4米，工程队单独整治的工期是工程队单独整治的工期的．

（1）问，工程队每天分别整治多少米？

（2）由，两个工程队先后接力完成，共用时40天，问，工程队分别整治多少米？

22．（10分）（1）如图1，在中，平分，且与的外角的角平分线交于点，若，，求的度数．

（2）如图2，在四边形中，平分，且与四边形的外角的角平分线交于点，若，，求的度数．

23．（11分）知识背景

我们在第十一章《三角形》中学习了三角形的边与角的性质，在第十二章《全等三角形》中学习了全等三角形的性质和判定，在第十三章《轴对称》中学习了等腰三角形的性质和判定．在一些探究题中经常用以上知识转化角和边，进而解决问题．

问题：如图1，是等腰三角形，，是的中点，以为腰作等腰，且满足，连接并延长交的延长线于点，试探究与之间的数量关系．

发现：（1）与之间的数量关系为　　．

探究：（2）如图2，当点是线段上任意一点（除、外）时，其他条件不变，试猜想与之间的数量关系，并证明你的结论．

拓展：（3）当点在线段的延长线上时，在备用图中补全图形，并直接写出的形状．

2019-2020学年河南省商丘市永城市八年级（上）期末数学试卷

参考答案与试题解析

一、选择题（每小题3分，共30分）在每个小题列出的四个选项中，只有一个是正确的，请把答题卡上对应题目所选的选项涂黑.

1．（3分）如图，已知，则一定是的　　

A．角平分线 B．高线 C．中线 D．无法确定

【解答】解：由于，则点是边的中点，所以一定是的一条中线．

故选：．

2．（3分）中国科学院微电子研究所微电子设备与集成技术领域的专家殷华湘说，他的团队已经研发出3纳米米纳米）晶体管．将3纳米换算成米用科学记数法表示为　　

A．米 B．米 C．米 D．米

【解答】解：3纳米米米；

故选：．

3．（3分）为你点赞，你是最棒的！下列四种表情图片都可以用来为你点赞！其中是轴对称图形的是　　

A． B． C． D．

【解答】解：由轴对称图形的概念可知第个是轴对称图形，第个，个与第个不是轴对称图形．

故选：．

4．（3分）在平面直角坐标系中，点与点关于轴对称，则在　　

A．第一象限 B．第二象限 C．第三象限 D．第四象限

【解答】解：由点与点关于轴对称，得

，．

故在第三象限．

故选：．

5．（3分）下列计算中，正确的是　　

A． B． C． D．

【解答】解：、，故原题计算错误；

、，故原题计算错误；

、，故原题计算错误；

、，故原题计算正确；

故选：．

6．（3分）如图，在中，，于点，，，则的度数为　　

A． B． C． D．

【解答】解：，，，

平分，

，

．

故选：．

7．（3分）如图，在中，，是的中点，是上任意一点，连接、并延长分别交、于点、，则图中的全等三角形共有　　

A．7对 B．6对 C．5对 D．4对

【解答】解：，是的中点，

，平分，

垂直平分，

，

，，，

；

，，，

；

，，，

，

，，

而，

；

，，

，，

，，，

，

，，，

，

，，，

．

故选：．

8．（3分）在中，为最大角，，，，则的取值范围是　　

A． B． C． D．

【解答】解：根据三角形的三边关系，得

，即．

为最大角，

为最长边，

．

故选：．

9．（3分）三个等边三角形的摆放位置如图所示，若，则的度数为　　

A． B． C． D．

【解答】解：如图，

，，，

，

，

故选：．

10．（3分）如图，在中，，，点、分别在边、上，，点是边上一动点，当的值最小时，，则为　　

A．30 B．29 C．28 D．27

【解答】解：作关于的对称点，连接，

则，

当的值最小时，最小，

当时，最小，

，，

，

，

，

，

，

，

，

，

解法二：作关于的对称点，连接，

则，

当的值最小时，最小，

当时，最小，

，，，

，

，

，

故选：．

二、填空题（每小题3分，共15分）

11．（3分）若分式的值为0，则的值为　0　．

【解答】解：，

，

解得．

故答案为：0．

12．（3分）因式分解：　　．

【解答】解：．

故答案为：．

13．（3分）如图，用一条宽度相等的足够长的纸条打一个结（如图，然后轻轻拉紧、压平就可以得到如图2所示的正五边形．在图2中，的度数为　　．

【解答】解：五边形是正五边形，

其每个内角为，且，

是等腰三角形，

，

．

故答案为：

14．（3分）如图，在中，，以点为圆心，适当的长为半径画弧，分别交、于点、，再分别以、为圆心，大于的长为半径画弧，两弧交于点，作射线，交于点．已知，，则的长为　2　．

【解答】解：由作法得平分，

，，

，

，

在中，，

在中，，

．

故答案为2．

15．（3分）如图，在中，，是线段上一个动点，把沿直线折叠，点落在同一平面内的处，当平行于的直角边时，的大小为　或　．

【解答】解：中，，

，，

把沿直线折叠，

，，

若，

，

，

，

，

若，

，且，

，

，

故答案为：或．

三、解答题（本大题共8个小题，满分75分）

16．（8分）计算：．

【解答】解：原式

．

17．（9分）先化简，再从，，1中选一个合适的数作为的值代入求值．

【解答】解：

，

，，

，，

，

当时，原式．

18．（9分）如图，在与中，，，与交于点．

（1）求证：．

（2）若，，求的周长．

【解答】（1）证明：，

与都是直角三角形，

在和中，，

，

；

（2）解：由（1）知，

，

，

的周长．

19．（9分）如图，在四边形中，，的平分线交的延长线于点，是的中点，连接并延长交于点．

（1）求证：平分．

（2）若，，求的度数．

【解答】（1）证明：平分，

．

，

，

，

，

是等腰三角形．

为的中点，

平分，

即平分．

（2）解：，

．

，

．

平分，

．

，，

．

20．（9分）如图，在中，，，，．

（1）求证：．

（2）猜想：与之间存在怎样的数量关系？请说明理由．

【解答】（1）证明：，，

，

，

即．

在和中，

，

．

（2）解：．

理由：由（1）得．

，，

，

．

21．（10分）现有一段360米长的河堤的整治任务，打算请，两个工程队来完成，经过调查发现，工程队每天比工程队每天多整治4米，工程队单独整治的工期是工程队单独整治的工期的．

（1）问，工程队每天分别整治多少米？

（2）由，两个工程队先后接力完成，共用时40天，问，工程队分别整治多少米？

【解答】解：（1）设工程队每天整治米，则工程队每天整治米．

根据题意，得：，

解得：，

经检验，是原分式方程的解，且符合题意，

．

答：工程队每天整治12米，工程队每天整治8米．

（2）设工程队整治了米，则工程队整治了米，

根据题意，得：，

解得：，

．

答：工程队整治河堤120米，工程队整治河堤240米．

22．（10分）（1）如图1，在中，平分，且与的外角的角平分线交于点，若，，求的度数．

（2）如图2，在四边形中，平分，且与四边形的外角的角平分线交于点，若，，求的度数．

【解答】解：（1）平分，平分，

，．

，，

，即，

．

，，，

．

（2）如图，延长，交于点．

，，

，

由（1）知．

23．（11分）知识背景

我们在第十一章《三角形》中学习了三角形的边与角的性质，在第十二章《全等三角形》中学习了全等三角形的性质和判定，在第十三章《轴对称》中学习了等腰三角形的性质和判定．在一些探究题中经常用以上知识转化角和边，进而解决问题．

问题：如图1，是等腰三角形，，是的中点，以为腰作等腰，且满足，连接并延长交的延长线于点，试探究与之间的数量关系．

发现：（1）与之间的数量关系为　　．

探究：（2）如图2，当点是线段上任意一点（除、外）时，其他条件不变，试猜想与之间的数量关系，并证明你的结论．

拓展：（3）当点在线段的延长线上时，在备用图中补全图形，并直接写出的形状．

【解答】解：（1）．理由：

是等腰三角形，且，

，．

，

，

，

．

是以为腰的等腰三角形，

．

在与中，，，，

，

．

，

，

，

，

，

．

故答案为：；

（2）．

理由：是等腰三角形，且，

，．

，

，

，

．

是以为腰的等腰三角形，

．

在与中，，，，

，

．

，

，

，

，

，

．

（3）是等腰直角三角形．理由：如备用图，

是等腰三角形，，

，．

，

，

，

．

是以为腰的等腰三角形，

．

在与中，，，，

，

．

，

，

，

，

，

是等腰三角形，

，

是等腰直角三角形．

声明：试题解析著作权属菁优网所有，未经书面同意，不得复制发布

日期：2021/12/9 14:46:00；用户：星星卷大葱；邮箱：jse035@xyh.com；学号：39024125