2018-2019学年重庆一中八年级（上）期末数学试卷

这是一份2018-2019学年重庆一中八年级（上）期末数学试卷，共25页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
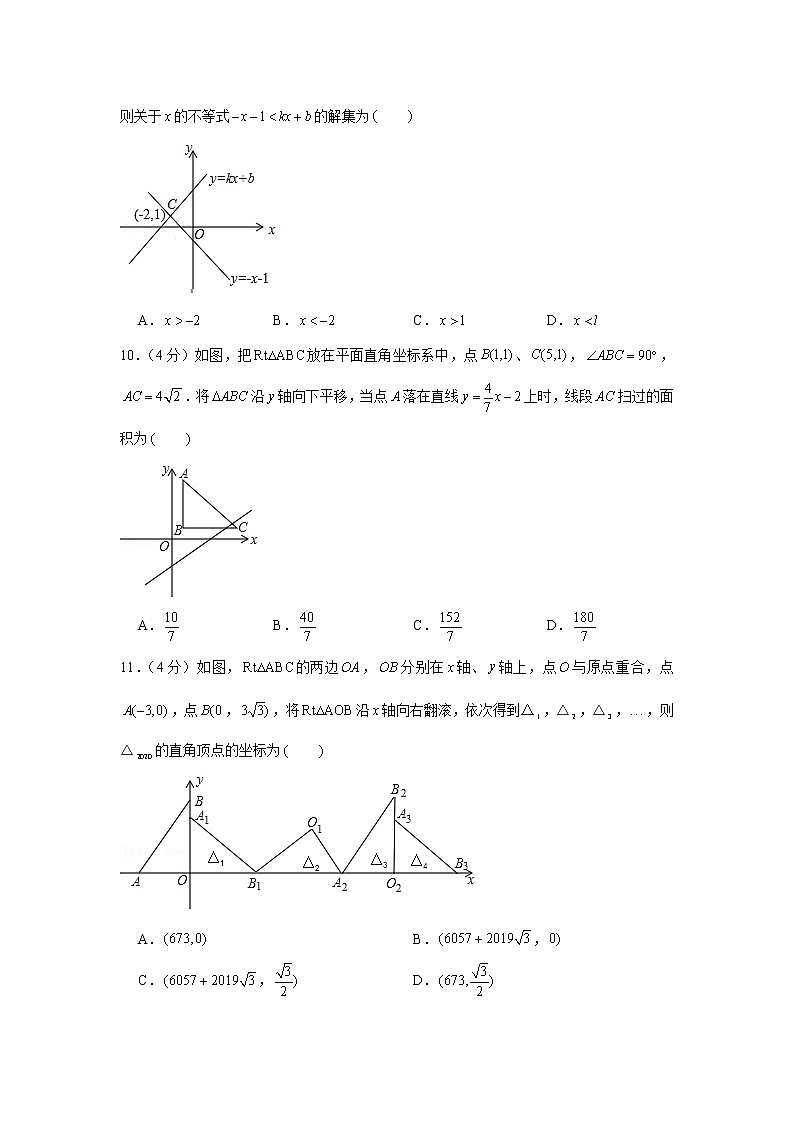
2018-2019学年重庆一中八年级（上）期末数学试卷一、选择题：（本大题共12个小题，每小题4分，共48分）在每个小题的下面，都给出了代号为A，B，C、D的四个答案，其中只有一个是正确的，请将各小题所选答案的代号填入答题卡相应的表格内1．（4分）下列各数中，是无理数的是　　A． B． C． D．0.32．（4分）下列图形中，既是轴对称图形，又是中心对称图形的是　　A． B． C． D．3．（4分）计算的结果是　　A． B． C． D．4．（4分）分式有意义，则的取值范围是　　A． B． C． D．5．（4分）三边长分别为、、，则下列条件不能判断是直角三角形的是　　A．，， B．，， C．，， D．，，6．（4分）下列命题是假命题的是　　A．两直线平行，同位角相等 B．全等三角形面积相等 C．直角三角形两锐角互余 D．若，那么，7．（4分）估计的值应在　　A．3和4之间 B．4和5之间 C．5和6之间 D．6和7之间8．（4分）如果直线与两坐标轴围成的三角形面积等于2，则的值是　　A． B． C． D．9．（4分）如图，直线与且，为常数）的交点坐标为，则关于的不等式的解集为　　A． B． C． D．10．（4分）如图，把放在平面直角坐标系中，点、，，．将沿轴向下平移，当点落在直线上时，线段扫过的面积为　　A． B． C． D．11．（4分）如图，的两边，分别在轴、轴上，点与原点重合，点，点，，将沿轴向右翻滚，依次得到△，△，△，，则△的直角顶点的坐标为　　A． B．， C．， D．12．（4分）已知整数使得关于、的二元一次方程组的解为正整数，且关于的不等式组有且仅有四个整数解，则所有满足条件的的和为　　A．4 B．9 C．10 D．12二、填空题：（本大题6个小题，每小题4分，共24分）请将正确答案填在答题卡相应的13．（4分）因式分解：　　．14．（4分）　　．15．（4分）一次函数的图象经过点，且与直线平行，则该一次函数解析式为　　．16．（4分）若，为实数，且，则的算术平方根为　　．17．（4分）甲、乙两人在同一直线道路上同起点、同方向、同时出发，分别以不同的速度匀速跑步1800米，当甲第一次超出乙300米时，甲停下来等候乙．甲、乙会合后，两人分别以原来的速度继续跑向终点，先到终点的人在终点休息．在整个跑步过程中，甲、乙两人之间的距离（米与乙出发的时间之间的关系如图所示则当甲到达终点时，乙跑了　　米．18．（4分）、、、、、六人按顺序围成一圈做游戏，每人抽一个数，已知每人按顺序抽到数字的两倍与其他五个人的平均数之差分别为9、10、13、15、23、30，则抽到的数字是　　．三、解答题（本大题2个小题，每小题8分，共16分）解答时每小题必须给出必要的演算过程或推理步骤19．（8分）解下列方程组或者不等式组（1）解方程组：（2）解不等式组：20．（8分）作图题：（不要求写作法）如图，在平面直角坐标系中，的三个顶点的坐标分别为，，．（1）作图：将先向右平移4个单位，再向下平移3个单位，则得到△，求作△；（2）求面积．四、解答题：（本大题4个小题，每小题10分，共40分）解答时每小题必须给出必要的演算过程或推理步骤21．（10分）重庆一中田径代表队在2018年重庆市青少年田径锦标赛上勇夺金牌8枚，银牌4枚，铜牌8枚，喜讯再次点燃了同学们热爱运动的热情为了解学生参与运动的情况，学校随机抽查了部分学生每日运动时间的情况，并将调查学生每日运动时间情况条形统计图学生每日运动时间情况扇形统计图．（1）被抽查的学生总数是　　人，并在图中补全条形统计图；（2）写出每日运动时间的中位数是　　小时，众数是　　小时；（3）求这批被调查学生平均每日运动的时间．22．（10分）如图，直线与直线相交于点，直线与轴交于点，直线与轴交于点，与轴交于点．（1）求交点的坐标；（2）求的面积．23．（10分）为了满足学生的需求，重庆一中超市准备购进甲、乙两种绿色袋装食品．其中甲乙两种绿色袋装食品的进价和售价如表： 甲乙进价（元袋）售价（元袋）2212已知：超市购进200袋甲种袋装食品或者购进300袋乙种袋装食品所用金额相等（1）求的值；（2）要使购进的甲、乙两种绿色袋装食品共1200袋的总利润（利润售价进价）不少于6400元，且不超过6420元，问该超市有哪几种进货方案？要获得最大利润该如何进货？（请写出具体方案）24．（10分）在中，，点为的中点，连接．（1）如图1，为线段延长线上的一点，连接，若，，，求；（2）如图2，点为上任意一点，过点作交于点，连接，取中点，连接和，求证：．五、解答题：（本大题2个小题，25题10分，26题12分，共22分）解答时每小题必须给出必要的演算过程或推理步骤25．（10分）阅读下列材料：对于一个任意四位正整数，若其千位数字与百位数字组成的两位数是它的十位数字与个位数字组成的两位数的两倍，则称这样的四位正整数为“双倍数”，如6231，其千位数字与百位数字组成的两位数为62，其十位数字与个位数字组成的两位数是31，62是31的两倍，则称6231为“双倍数”（1）猜想任意一个“双倍数”能否被67整除，并说明理由；（2）若一个双倍数的各个数位数字分别加上1组成一个新的四位正整数，这个新的四位正整数能被7整除，求所有满足条件的“双倍数”．26．（12分）如图，平面直角坐标系中直线与直线相交于点，直线与轴相交于点，与轴相交于点，点，点，，连接．（1）如图1，求点的坐标；（2）如图1，若将向轴的正方向平移个单位，得到△，点与点重合时停止移动，设△与重叠部分的面积为，请求出与的关系式，并写出的取值范围；（3）如图2，现将向轴的正方向平移12个单位得到△，直线与直线交于点，再将△绕点旋转，旋转角度为，记旋转后的三角形为△，直线与直线的交点为，直线与直线的交点为，是否存在为等腰三角形？若存在请直接写出的值；若不存在，请说明理由．
2018-2019学年重庆一中八年级（上）期末数学试卷参考答案与试题解析一、选择题：（本大题共12个小题，每小题4分，共48分）在每个小题的下面，都给出了代号为A，B，C、D的四个答案，其中只有一个是正确的，请将各小题所选答案的代号填入答题卡相应的表格内1．（4分）下列各数中，是无理数的是　　A． B． C． D．0.3【解答】解：．是无理数；．是分数，属于有理数；．是整数，属于有理数；．0.3是有限小数，即分数，属于有理数；故选：．2．（4分）下列图形中，既是轴对称图形，又是中心对称图形的是　　A． B． C． D．【解答】解：、不是轴对称图形，也不是中心对称图形，故此选项错误；、不是轴对称图形，是中心对称图形，故此选项错误；、是轴对称图形，也是中心对称图形，故此选项正确；、是轴对称图形，不是中心对称图形，故此选项错误．故选：．3．（4分）计算的结果是　　A． B． C． D．【解答】解：，故选：．4．（4分）分式有意义，则的取值范围是　　A． B． C． D．【解答】解：，．故选：．5．（4分）三边长分别为、、，则下列条件不能判断是直角三角形的是　　A．，， B．，， C．，， D．，，【解答】解：．，是直角三角形；．，不是直角三角形；．，是直角三角形；．，是直角三角形；故选：．6．（4分）下列命题是假命题的是　　A．两直线平行，同位角相等 B．全等三角形面积相等 C．直角三角形两锐角互余 D．若，那么，【解答】解：、两直线平行，同位角相等，所以选项的命题为真命题；、全等三角形面积相等，所以选项的命题为真命题；、直角三角形两锐角互余，所以选项的命题为真命题；、当，，所以选项的命题为假命题．故选：．7．（4分）估计的值应在　　A．3和4之间 B．4和5之间 C．5和6之间 D．6和7之间【解答】解：，，．故选：．8．（4分）如果直线与两坐标轴围成的三角形面积等于2，则的值是　　A． B． C． D．【解答】解：设直线与轴交于点，与轴交于点．当时，，点的坐标为；当时，，解得：．，，．故选：．9．（4分）如图，直线与且，为常数）的交点坐标为，则关于的不等式的解集为　　A． B． C． D．【解答】解：如图，直线与且，为常数）的交点坐标为，所以 关于的不等式的解集为．故选：．10．（4分）如图，把放在平面直角坐标系中，点、，，．将沿轴向下平移，当点落在直线上时，线段扫过的面积为　　A． B． C． D．【解答】解：点、，，，，，点的坐标为，将代入得，，线段扫过的面积为：，故选：．11．（4分）如图，的两边，分别在轴、轴上，点与原点重合，点，点，，将沿轴向右翻滚，依次得到△，△，△，，则△的直角顶点的坐标为　　A． B．， C．， D．【解答】解：．△的形状如同△△的直角顶点的纵坐标为0而△的直角顶点的横坐标为故选：．12．（4分）已知整数使得关于、的二元一次方程组的解为正整数，且关于的不等式组有且仅有四个整数解，则所有满足条件的的和为　　A．4 B．9 C．10 D．12【解答】解：解方程组得，方程组的解为正整数，，，6；解不等式组得，，不等式组有且仅有四个整数解，，，，5，6，所有满足条件的的和，故选：．二、填空题：（本大题6个小题，每小题4分，共24分）请将正确答案填在答题卡相应的13．（4分）因式分解：　　．【解答】解：，故答案为：．14．（4分）　　．【解答】解：原式．故答案为：．15．（4分）一次函数的图象经过点，且与直线平行，则该一次函数解析式为　　．【解答】解：设一次函数解析式为，把代入得，直线与直线平行，，一次函数解析式为．故答案为．16．（4分）若，为实数，且，则的算术平方根为　3　．【解答】解：依题意得：且，解得，所以，所以的算术平方根为：．故答案是：3．17．（4分）甲、乙两人在同一直线道路上同起点、同方向、同时出发，分别以不同的速度匀速跑步1800米，当甲第一次超出乙300米时，甲停下来等候乙．甲、乙会合后，两人分别以原来的速度继续跑向终点，先到终点的人在终点休息．在整个跑步过程中，甲、乙两人之间的距离（米与乙出发的时间之间的关系如图所示则当甲到达终点时，乙跑了　1380　米．【解答】解：由题意得乙的速度：（米秒），甲的速度： （米秒），两人相距时，甲跑的路程是（米，此时离终点距离为（米，从会合到终点甲的用时是（秒乙从会合点跑420秒路程是（米，当甲到终点时，乙跑的总路程是（米．故答案为：1380．18．（4分）、、、、、六人按顺序围成一圈做游戏，每人抽一个数，已知每人按顺序抽到数字的两倍与其他五个人的平均数之差分别为9、10、13、15、23、30，则抽到的数字是　15　．【解答】解：设、、、、、六人抽到的数分别为：，，，，，，由题意可得解得：故答案为：15三、解答题（本大题2个小题，每小题8分，共16分）解答时每小题必须给出必要的演算过程或推理步骤19．（8分）解下列方程组或者不等式组（1）解方程组：（2）解不等式组：【解答】解：（1）整理得①②得，解得，把代入②得，解得，所以方程组的解为；（2）解不等式①得，；解不等式②得，不等式组的解集为．20．（8分）作图题：（不要求写作法）如图，在平面直角坐标系中，的三个顶点的坐标分别为，，．（1）作图：将先向右平移4个单位，再向下平移3个单位，则得到△，求作△；（2）求面积．【解答】解：（1）如图所示，△即为所求；（2）如图，面积为：．四、解答题：（本大题4个小题，每小题10分，共40分）解答时每小题必须给出必要的演算过程或推理步骤21．（10分）重庆一中田径代表队在2018年重庆市青少年田径锦标赛上勇夺金牌8枚，银牌4枚，铜牌8枚，喜讯再次点燃了同学们热爱运动的热情为了解学生参与运动的情况，学校随机抽查了部分学生每日运动时间的情况，并将调查学生每日运动时间情况条形统计图学生每日运动时间情况扇形统计图．（1）被抽查的学生总数是　100　人，并在图中补全条形统计图；（2）写出每日运动时间的中位数是　　小时，众数是　　小时；（3）求这批被调查学生平均每日运动的时间．【解答】解：（1）被抽查的学生总数是人，每日运动时间为1.2小时的学生人数为人，补全条形统计图如图所示；故答案为：100；（2）每日运动时间的中位数是1小时，众数是1小时；故答案为：1，1；（3）这批被调查学生平均每日运动的时间小时．22．（10分）如图，直线与直线相交于点，直线与轴交于点，直线与轴交于点，与轴交于点．（1）求交点的坐标；（2）求的面积．【解答】解：（1）联立直线，的解析式成方程组，得：，解得：，交点的坐标为．（2）设直线与轴交于点，如图所示．当时，，，点的坐标为，点的坐标为，，，．当时，，解得：，点的坐标为，．，，．23．（10分）为了满足学生的需求，重庆一中超市准备购进甲、乙两种绿色袋装食品．其中甲乙两种绿色袋装食品的进价和售价如表： 甲乙进价（元袋）售价（元袋）2212已知：超市购进200袋甲种袋装食品或者购进300袋乙种袋装食品所用金额相等（1）求的值；（2）要使购进的甲、乙两种绿色袋装食品共1200袋的总利润（利润售价进价）不少于6400元，且不超过6420元，问该超市有哪几种进货方案？要获得最大利润该如何进货？（请写出具体方案）【解答】解：（1）依题意得：，解得：，（2）设购进甲种绿色袋装食品袋，表示出乙种绿色袋装食品袋，根据题意得，，解得：，是正整数，，共有4种方案；甲的利润大于乙的利润，要获得最大利润该应该进货时甲最大才行，即甲进货270袋，乙进货袋．24．（10分）在中，，点为的中点，连接．（1）如图1，为线段延长线上的一点，连接，若，，，求；（2）如图2，点为上任意一点，过点作交于点，连接，取中点，连接和，求证：．【解答】（1）解：，，是等边三角形，，，点为的中点，，，，，，是等腰直角三角形，，，，，；（2）证明：延长、交于点，如图2所示：，，，，，为的中点，，在和中，，，，．五、解答题：（本大题2个小题，25题10分，26题12分，共22分）解答时每小题必须给出必要的演算过程或推理步骤25．（10分）阅读下列材料：对于一个任意四位正整数，若其千位数字与百位数字组成的两位数是它的十位数字与个位数字组成的两位数的两倍，则称这样的四位正整数为“双倍数”，如6231，其千位数字与百位数字组成的两位数为62，其十位数字与个位数字组成的两位数是31，62是31的两倍，则称6231为“双倍数”（1）猜想任意一个“双倍数”能否被67整除，并说明理由；（2）若一个双倍数的各个数位数字分别加上1组成一个新的四位正整数，这个新的四位正整数能被7整除，求所有满足条件的“双倍数”．【解答】解：设正整数，其中、、、表示各个位置上的数字，且为0到9之间的整数，根据“双倍数”的定义，有．（1）假设是“双倍数”，则有，根据“双倍数”定义，有，则为整数，由此可见，任意一个“双倍数”都能被67整除；（2）由题意，新组成的四位正整数可表示为：因为，也就是可以整除7，而，所以需要“双倍数” 才可以整除7故所有满足这样条件的“双倍数”（用排除法）有：2613，4020，5427，8241，6834，9648．26．（12分）如图，平面直角坐标系中直线与直线相交于点，直线与轴相交于点，与轴相交于点，点，点，，连接．（1）如图1，求点的坐标；（2）如图1，若将向轴的正方向平移个单位，得到△，点与点重合时停止移动，设△与重叠部分的面积为，请求出与的关系式，并写出的取值范围；（3）如图2，现将向轴的正方向平移12个单位得到△，直线与直线交于点，再将△绕点旋转，旋转角度为，记旋转后的三角形为△，直线与直线的交点为，直线与直线的交点为，是否存在为等腰三角形？若存在请直接写出的值；若不存在，请说明理由．【解答】解：（1）由题意得，解得，．（2）在中，令，得，，令，，，在中，，，在中，，．分三种情况：①当时，如图1，交直线于点，则，，，即，，，②当时，如图2，，，，，，，③当时，如图3，，，易求得直线解析式为，，即，设与交于点，△．综上所述：（3）存在，或24．轴，，为等腰三角形时，或，分两种情况：①当时，必为等边三角形，如图4，此时旋转角或或，，，，，，，②当时，为等腰三角形，，如图5，此时旋转角或，．声明：试题解析著作权属菁优网所有，未经书面同意，不得复制发布日期：2021/12/10 11:27:10；用户：初中数学1；邮箱：jse032@xyh.com；学号：39024122