2022届高三数学一轮复习 微专题20 函数y=Asin(ωx φ)的图像及其应用（全国通用）

这是一份2022届高三数学一轮复习 微专题20 函数y=Asin(ωx φ)的图像及其应用（全国通用），共30页。试卷主要包含了的面积为等内容，欢迎下载使用。
微专题20 函数y=Asin(x+Φ)的图像及其应用

1．（2021·全国高考真题（理））把函数图像上所有点的横坐标缩短到原来的倍，纵坐标不变，再把所得曲线向右平移个单位长度，得到函数的图像，则（ ）
A． B．
C． D．
【答案】B
【解析】解法一：函数图象上所有点的横坐标缩短到原来的倍，纵坐标不变，得到的图象，再把所得曲线向右平移个单位长度，应当得到的图象，
根据已知得到了函数的图象，所以，
令，则，
所以，所以；
解法二：由已知的函数逆向变换，
第一步：向左平移个单位长度，得到的图象，
第二步：图象上所有点的横坐标伸长到原来的2倍，纵坐标不变，得到的图象，
即为的图象，所以.
故选：B.
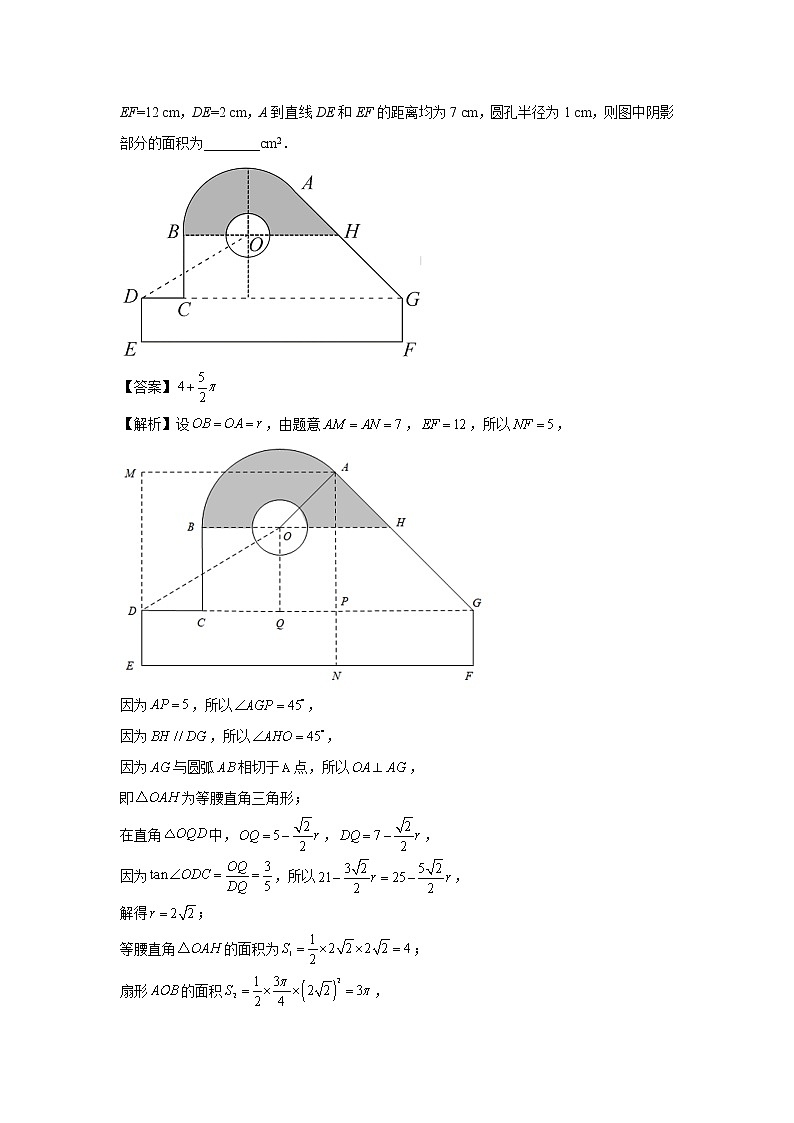
2．（2020·海南高考真题）某中学开展劳动实习，学生加工制作零件，零件的截面如图所示．O为圆孔及轮廓圆弧AB所在圆的圆心，A是圆弧AB与直线AG的切点，B是圆弧AB与直线BC的切点，四边形DEFG为矩形，BC⊥DG，垂足为C，tan∠ODC=，，EF=12 cm，DE=2 cm，A到直线DE和EF的距离均为7 cm，圆孔半径为1 cm，则图中阴影部分的面积为________cm2．

【答案】
【解析】设，由题意，，所以，

因为，所以，
因为，所以，
因为与圆弧相切于点，所以，
即为等腰直角三角形；
在直角中，，，
因为，所以，
解得；
等腰直角的面积为；
扇形的面积，
所以阴影部分的面积为.
故答案为：.
【点睛】本题主要考查三角函数在实际中应用，把阴影部分合理分割是求解的关键，以劳动实习为背景，体现了五育并举的育人方针.

1. 已知f(x)＝Asin(ωx＋φ)(A＞0，ω＞0)的部分图象求A的方法：
(1)利用极值点的纵坐标求A；(2)把某点的坐标代入求A.
2. 已知f(x)＝Asin(ωx＋φ)(A＞0，ω＞0)的部分图象求ω的方法：
由ω＝，即可求出ω.常用结论：(1)相邻两个极大（小）值点之间的距离为；(2)相邻两个零点之间的距离为；(3)极值点到相邻的零点，自变量取值区间长度为.
3.已知f(x)＝Asin(ωx＋φ)(A＞0，ω＞0)的部分图象求φ的方法：
求φ的值时最好选用最值点求．
峰点：ωx＋φ＝＋2kπ； 谷点：ωx＋φ＝－＋2kπ.
也可用零点求，但要区分该零点是升零点，还是降零点．
升零点(图象上升时与x轴的交点)：ωx＋φ＝2kπ；
降零点(图象下降时与x轴的交点)：ωx＋φ＝π＋2kπ(以上k∈Z)．
此外也可以把图象上的一个已知点代入(此时要注意该点在上升区间上还是在下降区间上)．

1.用五点法画y＝Asin(ωx＋φ)(A>0，ω>0，x∈R)一个周期内的简图，列表如下：
x





ωx＋φ
0

π

2π
2.三角函数的图象变换，有两种选择：一是先伸缩再平移，二是先平移再伸缩．函数y＝sinx的图象经变换得到y＝Asin(ωx＋φ)(A>0，ω>0)的图象的两种途径

【知识拓展】函数y＝Asin(ωx＋φ)(A>0，ω>0)的物理意义
简谐运动的图象所对应的函数解析式y＝Asin(ωx＋φ)，x∈[0，＋∞)，其中A>0，ω>0.在物理中，描述简谐运动的物理量，如振幅、周期和频率等都与这个解析式中的常数有关：A就是这个简谐运动的振幅，它是做简谐运动的物体离开平衡位置的最大距离；这个简谐运动的周期是T＝ ，这是做简谐运动的物体往复运动一次所需要的时间；这个简谐运动的频率由公式f＝给出，它是做简谐运动的物体在单位时间内往复运动的次数；ωx＋φ称为相位；x＝0时的相位φ称为初相．

1．（2021·四川省华蓥中学高三其他模拟（理））已知函数的最大值为2，其图象相邻两条对称轴之间的距离为且的图象关于点对称，则下列判断不正确的是（ ）
A．要得到函数的图象，只需将的图象向右平移个单位
B．函数的图象关于直线对称
C．时，函数的最小值为
D．函数在上单调递减
2．（2021·江苏省滨海中学高三其他模拟）第24届国际数学家大会会标是以我国古代数学家赵爽的弦图为基础进行设计的．如图，会标是由4个全等的直角三角形与一个小正方形拼成的一个大正方形，若小正方形的面积为4，大正方形的面积为100，设直角三角形中较大的锐角为，则（ ）．

A． B． C． D．
3．（2020·江苏高三一模）已知函数是奇函数，且的最小正周期为，将的图像上所有点的横坐标伸长到原来的2倍（纵坐标不变），所得图像对应的函数为，若，则__________.
4．（2021·上海静安区·高三一模）如图所示，在平面直角坐标系中，动点以每秒的角速度从点出发，沿半径为2的上半圆逆时针移动到，再以每秒的角速度从点沿半径为1的下半圆逆时针移动到坐标原点，则上述过程中动点的纵坐标关于时间的函数表达式为___________.


1．（2020·新疆高三三模（文））将函数的图象向右平移个单位，得到的图象，再将图象上的所有点的横坐标变成原来的，得到的图象，则下列说法正确的是（ ）
A．函数的最小正周期为
B．是函数图象的一个对称中心
C．函数图象的一个对称轴方程为
D．函数在区间上单调递增
2．（2021·全国高三其他模拟（理））已知函数，点为函数图象上的一个最高点，点，为函数的图象与轴相邻的两个交点．若周长的最小值为，且将函数的图象向右平移个单位后所得函数的图象恰好关于原点对称，则的值为（ ）
A． B． C． D．
3．（2021·全国高三其他模拟（文））已知函数()的图象向左平移个单位长度后得到函数的图象关于坐标原点对称，则的最小值为（ ）
A．1 B．2 C．3 D．4
4．（2021·全国高三其他模拟（理））已知函数，则下列结论正确的是（ ）
A．的图象关于点对称
B．在上的值域为
C．若，则，
D．将的图象向右平移个单位得的图象
5．（2021·全国高三其他模拟）（多选题）已知函数的图象向右平移个单位长度得的图象，则下列关于函数和的说法正确的是（ ）
A．函数与有相同的周期
B．函数的图象与函数的图象的对称中心一定不同
C．若函数的图象在上至少可取到两次最大值1，则
D．若函数的图象与直线在上恰有两个交点，则
6．（2021·重庆高三三模）（多选题）定义在实数集的函数的图象的一个最高点为，与之相邻的一个对称中心为，将的图象向右平移个单位长度得到函数的图象，则（ ）
A．的振幅为
B．的频率为
C．的单调递增区间为
D．在上只有一个零点
7．（2021·河北衡水中学高三其他模拟）（多选题）函数(，)的部分图像如图所示，则下列结论正确的是（ ）

A．
B．若把函数的图像向左平移个单位，则所得图像对应的函数是奇函数
C．若把的图像上所有点的横坐标变为原来的倍，纵坐标不变，得到图像对应的函数在上是增函数
D．，若成立，则的最小值为
8．（2021·全国高三其他模拟）将函数f（x）＝sin2x的图象向左平移个单位，得到函数的图象，则在区间 上的单调递减区间是 ___________.
9．（2021·江苏扬州市·扬州中学高三其他模拟）已知函数（，）的最小正周期为，将的图象向左平移（）个单位长度，所得函数为偶函数时，则的最小值是______．
10．（2021·山东高一期末）如图，一块边长为1的正方形区城，在处有一个可转动的探照灯，其照射角始终为，记探照灯照射在正方形内部区域（阴影部分）的面积为．若设，，则的最大值为______．

11．（2021·四川成都市·树德中学高三其他模拟（理））将函数图象上所有点向右平移个单位长度，然后横坐标缩短为原来的(纵坐标不变)，得到函数的图象.
（1）求函数的解析式及单调递增区间；
（2）在中，内角，，的对边分别为，，，若，，，且，求的面积.
12．（2021·浙江高三三模）已知函数的图象与y轴的交点坐标为(0，1)
（1）求的值；
（2）将图象向左平移个单位，再把其图象上每一个点的横坐标变为原来的2倍，纵坐标不变，得到的图象，求函数的最大值.

1．（2020·天津高考真题）已知函数．给出下列结论：
①的最小正周期为；
②是的最大值；
③把函数的图象上所有点向左平移个单位长度，可得到函数的图象．
其中所有正确结论的序号是（ ）
A．① B．①③ C．②③ D．①②③
2．（2019·天津高考真题（文））已知函数是奇函数，将的图像上所有点的横坐标伸长到原来的2倍（纵坐标不变），所得图像对应的函数为.若的最小正周期为，且，则
A． B． C． D．
3．（2018·天津高考真题（文））将函数的图象向右平移个单位长度，所得图象对应的函数
A．在区间 上单调递增 B．在区间 上单调递减
C．在区间 上单调递增 D．在区间 上单调递减
4．（2017·全国高考真题（理））已知曲线C1：y=cos x，C2：y=sin (2x+)，则下面结论正确的是
A．把C1上各点的横坐标伸长到原来的2倍，纵坐标不变，再把得到的曲线向右平移个单位长度，得到曲线C2
B．把C1上各点的横坐标伸长到原来的2倍，纵坐标不变，再把得到的曲线向左平移个单位长度，得到曲线C2
C．把C1上各点的横坐标缩短到原来的倍，纵坐标不变，再把得到的曲线向右平移个单位长度，得到曲线C2
D．把C1上各点的横坐标缩短到原来的倍，纵坐标不变，再把得到的曲线向左平移个单位长度，得到曲线C2
5．（2016·全国高考真题（理））若将函数y=2sin2x的图像向左平移个单位长度，则平移后图像的对称轴为
A．x=（k∈Z）
B．x=（k∈Z）
C．x=（k∈Z）
D．x=（k∈Z）
6．（2019·北京高考真题（文））如图，A，B是半径为2的圆周上的定点，P为圆周上的动点，是锐角，大小为β.图中阴影区域的面积的最大值为

A．4β+4cosβ B．4β+4sinβ C．2β+2cosβ D．2β+2sinβ
7.（2015·湖南高考真题（理））将函数的图像向右平移个单位后得到函数的图像，若对满足的，，有，则
A． B． C． D．
8．（2008·上海高考真题（理））某海域内有一孤岛，岛四周的海平面（视为平面）上有一浅水区（含边界），其边界是长轴长为2a，短轴长为2b的椭圆，已知岛上甲、乙导航灯的海拔高度分别为h1、h2，且两个导航灯在海平面上的投影恰好落在椭圆的两个焦点上，现有船只经过该海域（船只的大小忽略不计），在船上测得甲、乙导航灯的仰角分别为θ1、θ2，那么船只已进入该浅水区的判别条件是 　　 .

9．（2007·四川高考真题）下面有5个命题：
①函数的最小正周期是．
②终边在轴上的角的集合是．
③在同一坐标系中，函数的图象和函数的图象有3个公共点．
④把函数的图象向右平移得到的图象．
⑤函数在上是减函数．
其中，真命题的编号是___________（写出所有真命题的编号）
10．（2017·山东高考真题（理））设函数，其中.已知.
（Ⅰ）求；
（Ⅱ）将函数的图象上各点的横坐标伸长为原来的2倍（纵坐标不变），再将得到的图象向左平移个单位，得到函数的图象，求在上的最小值.
参考答案

1．（2021·四川省华蓥中学高三其他模拟（理））已知函数的最大值为2，其图象相邻两条对称轴之间的距离为且的图象关于点对称，则下列判断不正确的是（ ）
A．要得到函数的图象，只需将的图象向右平移个单位
B．函数的图象关于直线对称
C．时，函数的最小值为
D．函数在上单调递减
【答案】C
【解析】由题意得A=2，因为其图象相邻两条对称轴之间的距离为，
所以，可得，
所以，所以，
因为为对称中心，
所以，
因为，令k=0，可得，
所以.
对于A：将的图象向右平移个单位，
可得，故A正确；
对于B：令，解得，
令k=1，可得，所以函数的图象关于直线对称，故B正确；
对于C：因为，所以，
所以当时，，故C错误；
对于D：令，解得，
令k=0，可得一个单调减区间为，
因为，
所以函数在上单调递减，故D正确.
故选：C
2．（2021·江苏省滨海中学高三其他模拟）第24届国际数学家大会会标是以我国古代数学家赵爽的弦图为基础进行设计的．如图，会标是由4个全等的直角三角形与一个小正方形拼成的一个大正方形，若小正方形的面积为4，大正方形的面积为100，设直角三角形中较大的锐角为，则（ ）．

A． B． C． D．
【答案】B
【解析】解：根据题意，每个直角三角形的两条直角边的长度之差为2、斜边的长度为10，
故设直角三角形较大直角边为，则另一直角边为，
所以，解方程得：，
∴，，则，
∴．
故选：B.
【点睛】本题考查知识的迁移应用，解题的关键在于根据题意，发现每个直角三角形的两条直角边的长度之差为2、斜边的长度为10，进而列式计算，考查运算求解能力，是中档题.
3．（2020·江苏高三一模）已知函数是奇函数，且的最小正周期为，将的图像上所有点的横坐标伸长到原来的2倍（纵坐标不变），所得图像对应的函数为，若，则__________.
【答案】
【解析】函数是奇函数，则，
因为的最小正周期为，所以，
将的图像上所有点的横坐标变为原来的2倍(纵坐标不变)，
所得图像对应的函数为，
又，所以，解得，
所以
所以.
故答案为：
4．（2021·上海静安区·高三一模）如图所示，在平面直角坐标系中，动点以每秒的角速度从点出发，沿半径为2的上半圆逆时针移动到，再以每秒的角速度从点沿半径为1的下半圆逆时针移动到坐标原点，则上述过程中动点的纵坐标关于时间的函数表达式为___________.

【答案】
【解析】由三角函数的定义可得：当动点在半径为2的上半圆上运动时，，终边对应的角度为，所以点坐标为，
当动点在半径为1的下半圆上运动时，，终边对应的角度为，
所以点坐标为，
综上：动点的纵坐标关于时间的函数表达式为，
故答案为：
【点睛】本题主要考查利用三角函数的定义解决实际问题，在做题过程中点的坐标与角度之间的关系，从而帮助解题.

1．（2020·新疆高三三模（文））将函数的图象向右平移个单位，得到的图象，再将图象上的所有点的横坐标变成原来的，得到的图象，则下列说法正确的是（ ）
A．函数的最小正周期为
B．是函数图象的一个对称中心
C．函数图象的一个对称轴方程为
D．函数在区间上单调递增
【答案】D
【解析】，
则，
则，
所以的最小正周期为，故A错误；
，故不是函数图象的一个对称中心，故B错误；
，故不是函数图象的一个对称轴，故C错误；
当时，，此时的单调递增，故D正确.
故选：D.
2．（2021·全国高三其他模拟（理））已知函数，点为函数图象上的一个最高点，点，为函数的图象与轴相邻的两个交点．若周长的最小值为，且将函数的图象向右平移个单位后所得函数的图象恰好关于原点对称，则的值为（ ）
A． B． C． D．
【答案】D
【解析】由题意得，，解得，
所以，
所以，
因为的图象关于原点对称，
所以，即，
因为，所以．
故选：D
3．（2021·全国高三其他模拟（文））已知函数()的图象向左平移个单位长度后得到函数的图象关于坐标原点对称，则的最小值为（ ）
A．1 B．2 C．3 D．4
【答案】B
【解析】∵
∴.
又的图象关于坐标原点对称，∴，，
∴()，
∴当时，取得最小值，
故选：B.
4．（2021·全国高三其他模拟（理））已知函数，则下列结论正确的是（ ）
A．的图象关于点对称
B．在上的值域为
C．若，则，
D．将的图象向右平移个单位得的图象
【答案】D
【解析】，令，则，故，故A项错误，
当时，，，故B项错误，
因为的周期，所以若，则，，故C项错误，
将的图象向右平移个单位得的图象，故D项正确.
故选：D.
5．（2021·全国高三其他模拟）（多选题）已知函数的图象向右平移个单位长度得的图象，则下列关于函数和的说法正确的是（ ）
A．函数与有相同的周期
B．函数的图象与函数的图象的对称中心一定不同
C．若函数的图象在上至少可取到两次最大值1，则
D．若函数的图象与直线在上恰有两个交点，则
【答案】ACD
【解析】本题考查三角函数的图象和性质．函数的图象向右平移个单位长度得，所以函数与的周期都为，所以选项正确；函数的对称中心为，函数的对称中心为，当时，对称中心可以相同，所以选项不正确；若函数的图象在上至少可取到两次最大值1，则，解得，所以选项正确记，所以函数的图象与直线右边最近两个交点横坐标为和，左边最近两个交点横坐标为和，令，得，所以，所以正确．
故选：ACD.
6．（2021·重庆高三三模）（多选题）定义在实数集的函数的图象的一个最高点为，与之相邻的一个对称中心为，将的图象向右平移个单位长度得到函数的图象，则（ ）
A．的振幅为
B．的频率为
C．的单调递增区间为
D．在上只有一个零点
【答案】AD
【解析】由题意，可得，所以，可得，
所以，所以函数的振幅为3，故A正确；
函数的频率为，故B错误；
因为，所以，
因为，所以，即，
所以，
令，可得，
所以的单调递增区间为，而选项C只是其中一个单调递增区间，故C错误；
由，解得，
所以函数在上只有一个零点.
故选：AD
【点睛】本题主要考查了三角函数的图象变换，以及三角函数的图象与性质，其中解答中熟记三角函数的图象变换，以及熟练应用三角函数的图象与性质是解答的关键.
7．（2021·河北衡水中学高三其他模拟）（多选题）函数(，)的部分图像如图所示，则下列结论正确的是（ ）

A．
B．若把函数的图像向左平移个单位，则所得图像对应的函数是奇函数
C．若把的图像上所有点的横坐标变为原来的倍，纵坐标不变，得到图像对应的函数在上是增函数
D．，若成立，则的最小值为
【答案】AB
【解析】解析：由题图，知，
∴，∴.∵，即，
∴()，即()，
∵，∴，∴，故A正确；
把的图像向左平移个单位，所得图像对应的函数解析式为，是奇函数，故B正确：
把的图像上所有点的横坐标变为原来的，纵坐标不变，
得到图像对应的函数解析式为，∵，
∴在上不是增函数，故C错误；
，令
，，
所以，所以的最小值为，故D错误.
故选：AB.
8．（2021·全国高三其他模拟）将函数f（x）＝sin2x的图象向左平移个单位，得到函数的图象，则在区间 上的单调递减区间是 ___________.
【答案】
【解析】由题得，
因为，
因为在上单调递减，故由，得
所以在区间 上的单调递减区间是
故答案为：
9．（2021·江苏扬州市·扬州中学高三其他模拟）已知函数（，）的最小正周期为，将的图象向左平移（）个单位长度，所得函数为偶函数时，则的最小值是______．
【答案】
【解析】∵函数（，）的最小正周期为，
∴，．
将的图象向左平移（）个单位长度，所得函数的图象，
由于得到的函数为偶函数，
∴，，则的最小值是，
故答案为：．
10．（2021·山东高一期末）如图，一块边长为1的正方形区城，在处有一个可转动的探照灯，其照射角始终为，记探照灯照射在正方形内部区域（阴影部分）的面积为．若设，，则的最大值为______．

【答案】
【解析】解：因为，所以，
令，则，而，所以，

，当且仅当时取等号，
所以S的最大值为.
故答案为：.
11．（2021·四川成都市·树德中学高三其他模拟（理））将函数图象上所有点向右平移个单位长度，然后横坐标缩短为原来的(纵坐标不变)，得到函数的图象.
（1）求函数的解析式及单调递增区间；
（2）在中，内角，，的对边分别为，，，若，，，且，求的面积.
【答案】（1），单调递增区间；（2）.
【解析】（1），
图象向右平移个单位长度得到的图象，
横坐标缩短为原来的(纵坐标不变)得到图象，所以，
令，解得，
所以的单调递增区间为：
（2）由（1）知，，
因为，
所以，且，
当时，，，(舍去)
当时，，，
此时由余弦定理可知，，解得，
所以.
12．（2021·浙江高三三模）已知函数的图象与y轴的交点坐标为(0，1)
（1）求的值；
（2）将图象向左平移个单位，再把其图象上每一个点的横坐标变为原来的2倍，纵坐标不变，得到的图象，求函数的最大值.
【答案】（1）；（2）.
【解析】（1）由题意，函数，
可得，即，因为，所以.
（2）由（1）可知，函数，
将图象向左平移个单位，再把其图象上每一个点的横坐标变为原来的2倍，
纵坐标不变，可得，
所以
，
当时，函数取得最大值，最大值为.

1．（2020·天津高考真题）已知函数．给出下列结论：
①的最小正周期为；
②是的最大值；
③把函数的图象上所有点向左平移个单位长度，可得到函数的图象．
其中所有正确结论的序号是（ ）
A．① B．①③ C．②③ D．①②③
【答案】B
【解析】因为，所以周期，故①正确；
，故②不正确；
将函数的图象上所有点向左平移个单位长度，得到的图象，
故③正确.
故选：B.
【点晴】本题主要考查正弦型函数的性质及图象的平移，考查学生的数学运算能力，逻辑分析那能力，是一道容易题.
2．（2019·天津高考真题（文））已知函数是奇函数，将的图像上所有点的横坐标伸长到原来的2倍（纵坐标不变），所得图像对应的函数为.若的最小正周期为，且，则
A． B． C． D．
【答案】C
【解析】因为为奇函数，∴；
又
，，又
∴，
故选C．
【点睛】本题考查函数的性质和函数的求值问题，解题关键是求出函数．
3．（2018·天津高考真题（文））将函数的图象向右平移个单位长度，所得图象对应的函数
A．在区间 上单调递增 B．在区间 上单调递减
C．在区间 上单调递增 D．在区间 上单调递减
【答案】A
【解析】分析：首先确定平移之后的对应函数的解析式，然后逐一考查所给的选项是否符合题意即可.
详解：由函数图象平移变换的性质可知：
将的图象向右平移个单位长度之后的解析式为：
.
则函数的单调递增区间满足：，
即，
令可得函数的一个单调递增区间为，选项A正确，B错误；
函数的单调递减区间满足：，
即，
令可得函数的一个单调递减区间为，选项C，D错误；
本题选择A选项.
点睛：本题主要考查三角函数的平移变换，三角函数的单调区间等知识，意在考查学生的转化能力和计算求解能力.
4．（2017·全国高考真题（理））已知曲线C1：y=cos x，C2：y=sin (2x+)，则下面结论正确的是
A．把C1上各点的横坐标伸长到原来的2倍，纵坐标不变，再把得到的曲线向右平移个单位长度，得到曲线C2
B．把C1上各点的横坐标伸长到原来的2倍，纵坐标不变，再把得到的曲线向左平移个单位长度，得到曲线C2
C．把C1上各点的横坐标缩短到原来的倍，纵坐标不变，再把得到的曲线向右平移个单位长度，得到曲线C2
D．把C1上各点的横坐标缩短到原来的倍，纵坐标不变，再把得到的曲线向左平移个单位长度，得到曲线C2
【答案】D
【解析】把C1上各点的横坐标缩短到原来的倍，纵坐标不变，得到函数y=cos2x图象，再把得到的曲线向左平移个单位长度，得到函数y=cos2（x+）=cos（2x+）=sin（2x+）的图象，即曲线C2，
故选D．
点睛：三角函数的图象变换，提倡“先平移，后伸缩”，但“先伸缩，后平移”也常出现在题目中，所以也必须熟练掌握.无论是哪种变形，切记每一个变换总是对字母而言. 函数是奇函数；函数是偶函数；函数是奇函数；函数是偶函数.
5．（2016·全国高考真题（理））若将函数y=2sin2x的图像向左平移个单位长度，则平移后图像的对称轴为
A．x=（k∈Z）
B．x=（k∈Z）
C．x=（k∈Z）
D．x=（k∈Z）
【答案】B
【解析】由题意得，将函数的图象向左平移个单位长度，得到，由，得，即平移后的函数的对称轴方程为，故选B．
考点：三角函数的图象与性质．
【方法点晴】本题主要考查了三角函数的图象与性质，着重考查了三角函数的图象变换及三角函数的对称轴方程的求解，通过将函数的图象向左平移个单位长度，得到函数的解析式，即可求解三角函数的性质，同时考查了学生分析问题和解答问题的能力以及推理与运算能力．
6．（2019·北京高考真题（文））如图，A，B是半径为2的圆周上的定点，P为圆周上的动点，是锐角，大小为β.图中阴影区域的面积的最大值为

A．4β+4cosβ B．4β+4sinβ C．2β+2cosβ D．2β+2sinβ
【答案】B
【解析】观察图象可知，当P为弧AB的中点时，阴影部分的面积S取最大值，

此时∠BOP=∠AOP=π-β， 面积S的最大值为+S△POB+ S△POA=4β+
.
故选B.
【点睛】本题主要考查阅读理解能力、数学应用意识、数形结合思想及数学式子变形和运算求解能力，有一定的难度.关键观察分析区域面积最大时的状态，并将面积用边角等表示.
7.（2015·湖南高考真题（理））将函数的图像向右平移个单位后得到函数的图像，若对满足的，，有，则
A． B． C． D．
【答案】D
【解析】向右平移个单位后，得到，又∵，∴不妨
，，∴，又∵，
∴，故选D.
考点：三角函数的图象和性质.
【名师点睛】本题主要考查了三角函数的图象和性质，属于中档题，高考题对于三角函数的考查，多以
为背景来考查其性质，解决此类问题的关键：一是会化简，熟悉三角恒等变形，对三
角函数进行化简；二是会用性质，熟悉正弦函数的单调性，周期性，对称性，奇偶性等.
8．（2008·上海高考真题（理））某海域内有一孤岛，岛四周的海平面（视为平面）上有一浅水区（含边界），其边界是长轴长为2a，短轴长为2b的椭圆，已知岛上甲、乙导航灯的海拔高度分别为h1、h2，且两个导航灯在海平面上的投影恰好落在椭圆的两个焦点上，现有船只经过该海域（船只的大小忽略不计），在船上测得甲、乙导航灯的仰角分别为θ1、θ2，那么船只已进入该浅水区的判别条件是 　　 .

【答案】
【解析】依题意，.
故答案为 .
本题主要考查了椭圆的应用.考查了学生运用基础知识解决实际问题的能力
9．（2007·四川高考真题）下面有5个命题：
①函数的最小正周期是．
②终边在轴上的角的集合是．
③在同一坐标系中，函数的图象和函数的图象有3个公共点．
④把函数的图象向右平移得到的图象．
⑤函数在上是减函数．
其中，真命题的编号是___________（写出所有真命题的编号）
【答案】①④
【解析】①，正确；②错误；③，和在第一象限无交点，错误；④正确；⑤错误．故选①④．
10．（2017·山东高考真题（理））设函数，其中.已知.
（Ⅰ）求；
（Ⅱ）将函数的图象上各点的横坐标伸长为原来的2倍（纵坐标不变），再将得到的图象向左平移个单位，得到函数的图象，求在上的最小值.
【答案】(Ⅰ) .
(Ⅱ) .
【解析】（Ⅰ）利用两角和与差的三角函数化简得到
由题设知及可得.
（Ⅱ）由（Ⅰ）得
从而.
根据得到，进一步求最小值.
试题解析：（Ⅰ）因为，
所以



由题设知，
所以，.
故，，又，
所以.
（Ⅱ）由（Ⅰ）得
所以.
因为，
所以，
当，
即时，取得最小值.
【名师点睛】此类题目是三角函数问题中的典型题目，可谓相当经典.解答本题，关键在于能利用三角公式化简函数、进一步讨论函数的性质，本题易错点在于一是图象的变换与解析式的对应，二是忽视设定角的范围.难度不大，能较好的考查考生的基本运算求解能力及复杂式子的变形能力等.