2021-2022学年上学期深圳市初中数学七年级期末典型试卷1

这是一份2021-2022学年上学期深圳市初中数学七年级期末典型试卷1，共30页。

2021-2022学年上学期深圳市初中数学七年级期末典型试卷1
一．选择题（共10小题）
1．（2020秋•罗湖区校级期末）把方程中分母化整数，其结果应为（　　）
A． B．0
C． D．0
2．（2020秋•罗湖区校级期末）（﹣2）2004+3×（﹣2）2003的值为（　　）
A．﹣22003 B．22003 C．﹣22004 D．22004
3．（2020秋•龙华区期末）下列说法中正确的是（　　）
A．两点之间，直线最短
B．由两条射线组成的图形叫做角
C．若过多边形的一个顶点可以画5条对角线，则这个多边形是八边形
D．对于线段AC与BC，若AC＝BC，则点C是线段AB的中点
4．（2020秋•罗湖区校级期末）下列运算正确的是（　　）
A．2（a﹣1）＝2a﹣1 B．a2+a2＝2a2
C．﹣22＝4 D．﹣（a﹣b）+c＝﹣a﹣b+c
5．（2020秋•龙华区期末）地铁4号线在驶进深圳北站前，列车上共有a人，停靠深圳北站后，上车人数是下车人数的3倍，列车在驶离深圳北站时车上共有b人，那么在深圳北站上车的人数有（　　）
A．（a+b）人 B．（b﹣a）人 C．人 D．（b﹣a）人
6．（2020秋•罗湖区校级期末）若|a|＝﹣a，则实数a在数轴上的对应点一定在（　　）
A．原点左侧 B．原点右侧
C．原点或原点左侧 D．原点或原点右侧
7．（2020秋•罗湖区校级期末）下列四个说法：①角的两边越长，角就越大；②两点之间的所有连线中，线段最短；③如果AB＝BC，则点B是线段AC的中点；④在平面内，经过两点有且只有一条直线．其中正确的是（　　）
A．①② B．①③ C．②③ D．②④
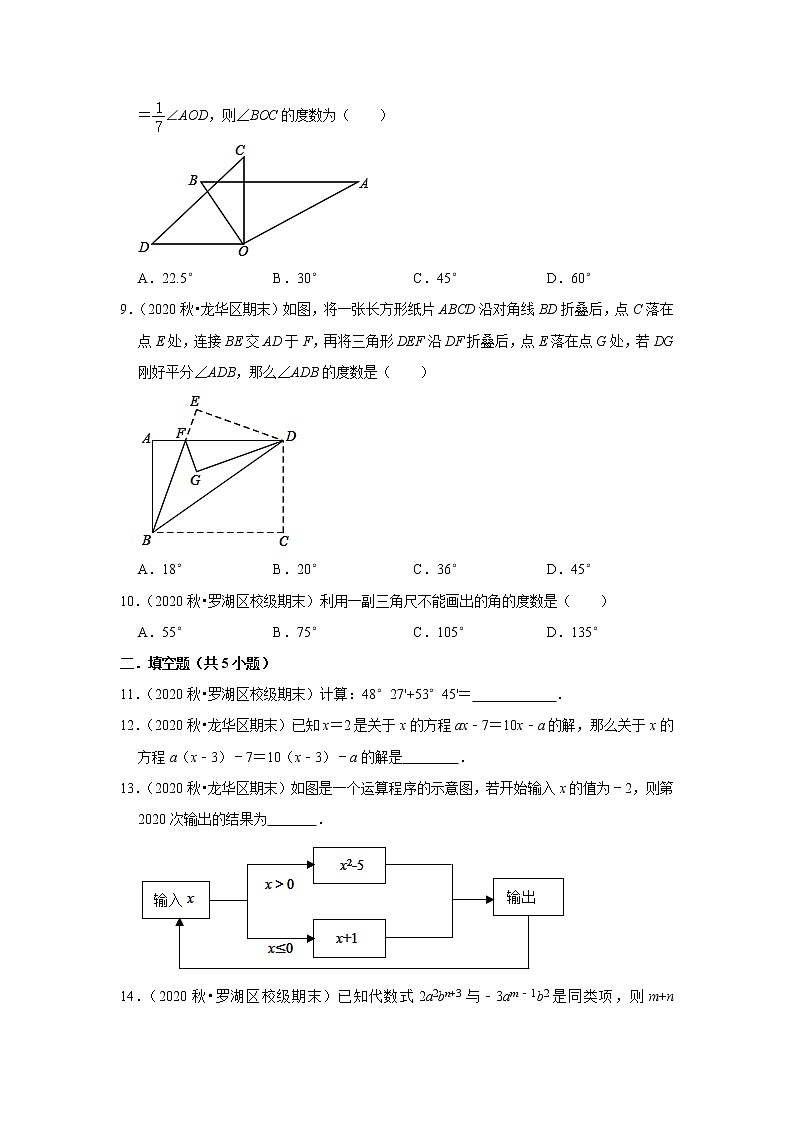
8．（2020秋•罗湖区校级期末）如图，两块直角三角板的直角顶点O重合在一起，若∠BOC＝∠AOD，则∠BOC的度数为（　　）

A．22.5° B．30° C．45° D．60°
9．（2020秋•龙华区期末）如图，将一张长方形纸片ABCD沿对角线BD折叠后，点C落在点E处，连接BE交AD于F，再将三角形DEF沿DF折叠后，点E落在点G处，若DG刚好平分∠ADB，那么∠ADB的度数是（　　）

A．18° B．20° C．36° D．45°
10．（2020秋•罗湖区校级期末）利用一副三角尺不能画出的角的度数是（　　）
A．55° B．75° C．105° D．135°
二．填空题（共5小题）
11．（2020秋•罗湖区校级期末）计算：48°27'+53°45'＝　 　．
12．（2020秋•龙华区期末）已知x＝2是关于x的方程ax﹣7＝10x﹣a的解，那么关于x的方程a（x﹣3）﹣7＝10（x﹣3）﹣a的解是　 　．
13．（2020秋•龙华区期末）如图是一个运算程序的示意图，若开始输入x的值为﹣2，则第2020次输出的结果为　 　．

14．（2020秋•罗湖区校级期末）已知代数式2a2bn+3与﹣3am﹣1b2是同类项，则m+n＝　 　．
15．（2020秋•龙华区期末）一个几何体由若干大小相同的小立方块搭成，如图分别是从它的正面、上面看到的形状图，那么搭成该几何体至少需用小立方块　 　个．

三．解答题（共7小题）
16．（2020秋•罗湖区校级期末）计算：
（1）（﹣）×2+（﹣2）÷（﹣15）．
（2）（﹣）2×6﹣（﹣2）3×（﹣）．
（3）÷（﹣1）﹣32×（﹣1+）．
（4）3（2x﹣3y+1）﹣2（4x+2y﹣3）．
（5）2a2﹣[3a2+4（﹣a2+2a）﹣2]．
17．（2020秋•罗湖区校级期末）解方程
（1）﹣6x+2＝2x﹣6
（2）
18．（2020秋•罗湖区校级期末）先化简，再求值：已知（a﹣1）2+|b+2|＝0，求代数式（6a2﹣2ab）﹣2（3a2+4ab）的值．
19．（2020秋•罗湖区校级期末）如图，直线AB、CD相交于点O，OE平分∠AOC，∠BOD＝62°，OF⊥OD．求∠EOF的度数．

20．（2020秋•龙华区期末）某校为防疫需要，实行错时错峰测温并开通专用通道上学，该校七、八年级人数如下表所示：
年级
人数（人）
七年级
620
八年级
450
①八年级学生进校时同时开通了A、B两通道，经过6分钟，八年级全部学生进校，已知A通道每分钟通过的人数是B通道每分钟通过人数的2倍．求A、B通道每分钟通过的人数各是多少人？
②考虑到七年级人数更多的原因，为节约学生进校时间，学校决定在A通道旁边增开C通道，在B通道旁边增开D通道，已知C通道每分钟通过的人数比A通道每分钟通过的人数多20%，D通道每分钟通过的人数比B通道每分钟通过的人数少20%，求七年级全部学生进校所需时间是多少分钟？
21．（2021•罗湖区校级模拟）如图，已知数轴上原点为O，点B表示的数为﹣2，A在B的右边，且A与B的距离是5，动点P从点B出发，以每秒3个单位长度的速度沿数轴向右匀速运动，动点Q从点A出发，以每秒4个单位长度的速度沿数轴向左匀速运动，若点P、Q同时出发，设运动时间为t（t＞0）秒．

（1）写出数轴上点A表示的数　 　，点P表示的数　 　（用含t的代数式表示），点Q表示的数　 　（用含t的代数式表示）；
（2）问点P与点Q何时到点O距离相等？
（3）若点D是数轴上一点，点D表示的数是x，是否存在x，使得|x﹣3|+|x+2|＝7？如果存在，直接写出x的值：如果不存在，说明理由．
22．（2020秋•龙华区期末）定义：在数轴上，如果两个数所对应点位于某点的两侧，且与这点的距离相等，我们称其中一个数与另一个数关于这点互为对称数，例如，如图，数1在数轴上所对应点为点A，则数4与数﹣2关于点A互为对称数；已知点P是数轴上一动点，数﹣1与﹣4关于点P互为对称数分别为m、n，数m与数n在数轴上对应的点分别为点M、N．
（1）当点P运动至原点O时，m＝　 　，n＝　 　；
（2）若点P运动至与点A时，m＝　 　，n＝　 　；
（3）若点P运动至与数t所对应的点时，m＝　 　，n＝　 　；（用含t的代数式表示）
（4）在（3）中，数t＝　 　时，点P、M，N三点中恰有一点是另两点连线段的中点．


2021-2022学年上学期深圳市初中数学七年级期末典型试卷1
参考答案与试题解析
一．选择题（共10小题）
1．（2020秋•罗湖区校级期末）把方程中分母化整数，其结果应为（　　）
A． B．0
C． D．0
【考点】解一元一次方程．
【专题】计算题．
【分析】方程两边同乘以10化分母为整数，乘的时候分母及分子都要乘以10．
【解答】解：根据分式的性质，每个分式分子分母同乘以10得：．
故选：C．
【点评】本题考查了化分母为整数，注意方程两边每一项都要同乘以同一个数．注意分式的基本性质与等式的性质的不同点．
2．（2020秋•罗湖区校级期末）（﹣2）2004+3×（﹣2）2003的值为（　　）
A．﹣22003 B．22003 C．﹣22004 D．22004
【考点】有理数的乘方．
【专题】计算题．
【分析】（﹣2）2004可以表示为（﹣2）（﹣2）2003，可以提取（﹣2）2003，即可求解．
【解答】解：原式＝（﹣2）（﹣2）2003+3×（﹣2）2003，
＝（﹣2）2003（﹣2+3），
＝（﹣2）2003，
＝﹣22003．
故选：A．
【点评】本题主要考查了有理数的乘方的性质，（﹣a）2n＝a2n，（﹣a）2n+1＝﹣a2n+1，正确提取是解决本题的关键．
3．（2020秋•龙华区期末）下列说法中正确的是（　　）
A．两点之间，直线最短
B．由两条射线组成的图形叫做角
C．若过多边形的一个顶点可以画5条对角线，则这个多边形是八边形
D．对于线段AC与BC，若AC＝BC，则点C是线段AB的中点
【考点】直线、射线、线段；线段的性质：两点之间线段最短；两点间的距离；角的概念；多边形的对角线．
【专题】线段、角、相交线与平行线；多边形与平行四边形；几何直观；运算能力．
【分析】根据两点之间线段最短，角的定义，多边形的对角线以及线段中点的定义对各小题分析判断即可得解
【解答】解：A、两点之间，线段最短，故本选项不合题意；
B、有公共端点是两条射线组成的图形叫做角，故本选项不合题意；
C、若过多边形的一个顶点可以画5条对角线，则这个多边形是八边形，故本选项符合题意；
D、若线段AC＝BC，则点C是线段AB的中点，错误，A、B、C三点不一定共线，故本选项不合题意；
故选：C．
【点评】本题考查了两点之间线段最短，角的定义，线段中点的定义，多边形的对角线，熟练掌握概念是解题的关键．
4．（2020秋•罗湖区校级期末）下列运算正确的是（　　）
A．2（a﹣1）＝2a﹣1 B．a2+a2＝2a2
C．﹣22＝4 D．﹣（a﹣b）+c＝﹣a﹣b+c
【考点】有理数的乘方；整式的加减．
【专题】整式；运算能力．
【分析】直接利用整式的加减运算法则以及有理数的乘方运算法则分别判断得出答案．
【解答】解：A、2（a﹣1）＝2a﹣2，故此选项错误；
B、a2+a2＝2a2，正确；
C、﹣22＝﹣4，故此选项错误；
D、﹣（a﹣b）+c＝﹣a+b+c，故此选项错误；
故选：B．
【点评】此题主要考查了整式的加减，正确掌握相关运算法则是解题关键．
5．（2020秋•龙华区期末）地铁4号线在驶进深圳北站前，列车上共有a人，停靠深圳北站后，上车人数是下车人数的3倍，列车在驶离深圳北站时车上共有b人，那么在深圳北站上车的人数有（　　）
A．（a+b）人 B．（b﹣a）人 C．人 D．（b﹣a）人
【考点】列代数式．
【专题】整式；应用意识．
【分析】设下车人数为x，则上车人数为3x，列出等量关系式，求出x，即可得出上车的人数．
【解答】解：设下车人数为x，则上车人数为3x，
a+3x﹣x＝b，
∴x＝，
∴上车的人数为，
故选：D．
【点评】本题主要考查列代数式，弄清题中的数量关系是解题的关键．
6．（2020秋•罗湖区校级期末）若|a|＝﹣a，则实数a在数轴上的对应点一定在（　　）
A．原点左侧 B．原点右侧
C．原点或原点左侧 D．原点或原点右侧
【考点】数轴；绝对值．
【专题】实数；几何直观．
【分析】根据|a|＝﹣a，求出a的取值范围，再根据数轴的特点进行解答即可求出答案．
【解答】解：∵|a|＝﹣a≥0，
∴a≤0，
∴实数a在数轴上的对应点一定在原点或原点左侧．
故选：C．
【点评】此题考查了绝对值与数轴，数轴上某个数与原点的距离叫做这个数的绝对值．
7．（2020秋•罗湖区校级期末）下列四个说法：①角的两边越长，角就越大；②两点之间的所有连线中，线段最短；③如果AB＝BC，则点B是线段AC的中点；④在平面内，经过两点有且只有一条直线．其中正确的是（　　）
A．①② B．①③ C．②③ D．②④
【考点】直线、射线、线段；直线的性质：两点确定一条直线；线段的性质：两点之间线段最短；两点间的距离；角的概念．
【专题】线段、角、相交线与平行线；几何直观．
【分析】利用确定直线的条件、线段的性质、角的概念及线段中点的定义分别判断，即可确定正确的选项．
【解答】解：①角的大小与边的长短无关，故角的两边越长，角就越大是错误的；
②两点之间的所有连线中，线段最短，正确；
③若AB＝BC，点A、B、C不一定在同一直线上，所以点B不一定是线段AC的中点，故错误．
④在平面内，经过两点有且只有一条直线，正确．
故选：D．
【点评】本题考查了直线的性质，线段的性质，余角的性质，中点的定义，熟记概念和性质是解题的关键．
8．（2020秋•罗湖区校级期末）如图，两块直角三角板的直角顶点O重合在一起，若∠BOC＝∠AOD，则∠BOC的度数为（　　）

A．22.5° B．30° C．45° D．60°
【考点】角的计算．
【专题】线段、角、相交线与平行线．
【分析】此题由“两块直角三角板”可知∠DOC＝∠BOA＝90°，根据同角的余角相等可以证明∠DOB＝∠AOC，由题意设∠BOC＝x°，则∠AOD＝7x°，结合图形列方程即可求解．
【解答】解：由两块直角三角板的直顶角O重合在一起可知：∠DOC＝∠BOA＝90°，
∴∠DOB+∠BOC＝90°，∠AOC+∠BOC＝90°，
∴∠DOB＝∠AOC，
设∠BOC＝x°，则∠AOD＝7x°，
∴∠DOB+∠AOC＝∠AOD﹣∠BOC＝6x°，
∴∠DOB＝3x°，
∴∠DOB+∠BOC＝4x°＝90°，
解得：x＝22.5．
故选：A．
【点评】此题主要考查有关角的推理和运算，理清图中的角的和差关系，并结合方程求解是解题的关键．
9．（2020秋•龙华区期末）如图，将一张长方形纸片ABCD沿对角线BD折叠后，点C落在点E处，连接BE交AD于F，再将三角形DEF沿DF折叠后，点E落在点G处，若DG刚好平分∠ADB，那么∠ADB的度数是（　　）

A．18° B．20° C．36° D．45°
【考点】角的计算．
【专题】线段、角、相交线与平行线；运算能力．
【分析】根据折叠的性质可得∠BDC＝∠BDE，∠EDF＝∠GDF，由角平分线的定义可得∠BDA＝∠GDF+∠BDG＝2∠GDF，然后根据矩形的性质及角的运算可得答案．
【解答】解：由折叠可知，∠BDC＝∠BDE，∠EDF＝∠GDF，
∵DG平分∠ADB，
∴∠BDG＝∠GDF，
∴∠EDF＝∠BDG，
∴∠BDE＝∠EDF+∠GDF+∠BDG＝3∠GDF，
∴∠BDC＝∠BDE＝3∠GDF，
∠BDA＝∠GDF+∠BDG＝2∠GDF，
∵∠BDC+∠BDA＝90°＝3∠GDF+2∠GDF＝5∠GDF，
∴∠GDF＝18°，
∴∠ADB＝2∠GDF＝2×18°＝36°．
故选：C．
【点评】此题考查的是角的运算及角平分线的定义，正确掌握折叠的性质是解决此题的关键．
10．（2020秋•罗湖区校级期末）利用一副三角尺不能画出的角的度数是（　　）
A．55° B．75° C．105° D．135°
【考点】角的计算．
【专题】线段、角、相交线与平行线；几何直观；应用意识．
【分析】一副三角尺中角有：30°、45°、60°、90°，这些度数的和或差，均可以用它画出，否则不能．
【解答】解：因为一副三角尺中角有：30°、45°、60°、90°，
因此这些度数的和或差，均可以画出，
如：75°＝30°+45°，105°＝60°+45°，135°＝90°+45°，
只有A不能写成上述角度的和或差，
故选：A．
【点评】考查角的意义，以及角的和与差，把一个角写成三角板中含有的角的和或差是正确判断的前提．
二．填空题（共5小题）
11．（2020秋•罗湖区校级期末）计算：48°27'+53°45'＝　102°12′　．
【考点】度分秒的换算．
【专题】线段、角、相交线与平行线；运算能力．
【分析】利用度加度，分加分，然后满60′往前进1°即可．
【解答】解：原式＝101°72′＝102°12′，
故答案为：102°12′．
【点评】此题主要考查了度分秒的换算，关键是掌握60′＝1°．
12．（2020秋•龙华区期末）已知x＝2是关于x的方程ax﹣7＝10x﹣a的解，那么关于x的方程a（x﹣3）﹣7＝10（x﹣3）﹣a的解是　x＝5　．
【考点】一元一次方程的解．
【专题】一次方程（组）及应用；运算能力．
【分析】把x＝2代入方程，即可求出a的值，然后代入a（x﹣3）﹣7＝10（x﹣3）﹣a并解方程．
【解答】解：把x＝2代入方程ax﹣7＝10x﹣a，得2a﹣7＝20﹣a．
解得a＝9．
所以由a（x﹣3）﹣7＝10（x﹣3）﹣a，得9（x﹣3）﹣7＝10（x﹣3）﹣9．
解得x＝5．
故答案是：x＝5．
【点评】本题考查了解一元一次方程和一元一次方程的解，能得出关于a的一元一次方程是解此题的关键．
13．（2020秋•龙华区期末）如图是一个运算程序的示意图，若开始输入x的值为﹣2，则第2020次输出的结果为　﹣4　．

【考点】有理数的混合运算；代数式求值．
【专题】整式；运算能力．
【分析】依次求出每次输出的结果，根据结果得出规律，即可得出答案．
【解答】解：第一次输入：∵x＝﹣2＜0，
∴x+1＝﹣2+1＝﹣1，
第二次输入：∵﹣1＜0，
∴x+1＝﹣1+1＝0；
第三次输入：∴x+1＝0+1＝1，
第四次输入：∵1＞0，
∴x2﹣5＝12﹣5＝﹣4，
第五次输入：∵﹣4≤0，
∴x+1＝﹣4+1＝﹣3，
第六次输入：∵﹣3＜0，
∴x+1＝﹣3+1＝﹣2，
第七次输入：∵﹣2＜0，
∴x+1＝﹣2+1＝﹣1，
……
依此类推，
2020÷6＝336…4，
所以输出的结果是﹣4，
故答案为：﹣4．
【点评】本题考查了求代数式的值，能根据求出的结果得出规律是解此题的关键．
14．（2020秋•罗湖区校级期末）已知代数式2a2bn+3与﹣3am﹣1b2是同类项，则m+n＝　2　．
【考点】同类项．
【专题】整式；运算能力．
【分析】直接利用同类项的定义得出m，n的值，进而得出答案．
【解答】解：∵代数式2a2bn+3与﹣3am﹣1b2是同类项，
∴m﹣1＝2，n+3＝2，
解得：m＝3，n＝﹣1，
则m+n＝3﹣1＝2．
故答案为：2．
【点评】此题主要考查了同类项，正确把握同类项的定义是解题关键．
15．（2020秋•龙华区期末）一个几何体由若干大小相同的小立方块搭成，如图分别是从它的正面、上面看到的形状图，那么搭成该几何体至少需用小立方块　6　个．

【考点】简单组合体的三视图；由三视图判断几何体．
【专题】投影与视图；空间观念；几何直观；推理能力．
【分析】根据题意可以得到该几何体从正面和上面看至少有多少个小立方体，综合考虑即可解答本题．
【解答】解：根据主视图可得，俯视图中第一列中至少一处有2层；
所以该几何体至少是用6个小立方块搭成的．
故答案为：6．
【点评】本题考查了由三视图判断几何体，由三视图想象几何体的形状，应分别根据主视图、俯视图和左视图想象几何体的前面、上面和左侧面的形状，然后综合起来考虑整体形状．
三．解答题（共7小题）
16．（2020秋•罗湖区校级期末）计算：
（1）（﹣）×2+（﹣2）÷（﹣15）．
（2）（﹣）2×6﹣（﹣2）3×（﹣）．
（3）÷（﹣1）﹣32×（﹣1+）．
（4）3（2x﹣3y+1）﹣2（4x+2y﹣3）．
（5）2a2﹣[3a2+4（﹣a2+2a）﹣2]．
【考点】有理数的混合运算；整式的加减．
【专题】整式；运算能力．
【分析】（1）直接利用有理数的混合运算法则计算得出答案；
（2）直接利用有理数的混合运算法则计算得出答案；
（3）直接利用有理数的混合运算法则计算得出答案；
（4）直接去括号进而合并同类项得出答案；
（5）直接去括号进而合并同类项得出答案．
【解答】解：（1）（﹣）×2+（﹣2）÷（﹣15）
＝﹣×+×
＝﹣+
＝；

（2）（﹣）2×6﹣（﹣2）3×（﹣）
＝×6﹣8×
＝﹣2
＝；

（3）÷（﹣1）﹣32×（﹣1+）
＝×（﹣）﹣9×（﹣）
＝﹣+
＝；

（4）3（2x﹣3y+1）﹣2（4x+2y﹣3）
＝6x﹣9y+3﹣8x﹣4y+6
＝﹣2x﹣13y+9；

（5）2a2﹣[3a2+4（﹣a2+2a）﹣2]
＝2a2﹣3a2﹣4（﹣a2+2a）+2
＝3a2﹣8a+2．
【点评】此题主要考查了整式的加减以及有理数的混合运算，正确合并同类项是解题关键．
17．（2020秋•罗湖区校级期末）解方程
（1）﹣6x+2＝2x﹣6
（2）
【考点】解一元一次方程．
【专题】一次方程（组）及应用；运算能力．
【分析】（1）移项、合并同类项、系数化为1，据此求出方程的解是多少即可．
（2）去分母、去括号、移项、合并同类项、系数化为1，据此求出方程的解是多少即可．
【解答】解：（1）移项，合并同类项，可得：﹣8x＝﹣8，
系数化为1，可得：x＝1．

（2）去分母，可得：2（1﹣2x）＝3（3x+1），
去括号，可得：2﹣4x＝9x+3，
移项，合并同类项，可得：﹣13x＝1，
系数化为1，可得：x＝﹣．
【点评】此题主要考查了解一元一次方程的方法，要熟练掌握，解一元一次方程的一般步骤：去分母、去括号、移项、合并同类项、系数化为1．
18．（2020秋•罗湖区校级期末）先化简，再求值：已知（a﹣1）2+|b+2|＝0，求代数式（6a2﹣2ab）﹣2（3a2+4ab）的值．
【考点】非负数的性质：绝对值；非负数的性质：偶次方；整式的加减—化简求值．
【专题】整式；运算能力．
【分析】化简代数式，先去括号，然后合并同类项，根据绝对值和乘方的非负性求得a，b的值，代入求值即可．
【解答】解：（6a2﹣2ab）﹣2 （3a2+4ab﹣b2）
＝6a2﹣2ab﹣6a2﹣8ab+b2
＝﹣10ab+b2，
∵（a﹣1）2+|b+2|＝0，
∴a﹣1＝0，b+2＝0，即a＝1，b＝﹣2，
∴原式＝20+1＝21．
【点评】本题考查整式的化简求值，掌握去括号及有理数的混合运算法则正确化简计算是本题的解题关键．
19．（2020秋•罗湖区校级期末）如图，直线AB、CD相交于点O，OE平分∠AOC，∠BOD＝62°，OF⊥OD．求∠EOF的度数．

【考点】角平分线的定义；对顶角、邻补角；垂线．
【专题】线段、角、相交线与平行线；运算能力．
【分析】依据对顶角的性质以及角平分线的定义，即可得到∠COE的度数，再根据垂线的定义，即可得到∠EOF的度数．
【解答】解：∵∠AOC与∠BOD是对顶角，
∴∠AOC＝∠BOD＝62°，
∵OE平分∠AOC，
∴∠COE＝∠AOC＝×62°＝31°，
∵OF⊥OD，
∴∠COF＝∠DOF＝90°，
∴∠EOF+∠COE＝90°，
∴∠EOF＝90°﹣∠COE＝90°﹣31°＝59°．
【点评】本题考查了对顶角相等，角平分线的定义，熟记性质与概念并准确识图是解题的关键．
20．（2020秋•龙华区期末）某校为防疫需要，实行错时错峰测温并开通专用通道上学，该校七、八年级人数如下表所示：
年级
人数（人）
七年级
620
八年级
450
①八年级学生进校时同时开通了A、B两通道，经过6分钟，八年级全部学生进校，已知A通道每分钟通过的人数是B通道每分钟通过人数的2倍．求A、B通道每分钟通过的人数各是多少人？
②考虑到七年级人数更多的原因，为节约学生进校时间，学校决定在A通道旁边增开C通道，在B通道旁边增开D通道，已知C通道每分钟通过的人数比A通道每分钟通过的人数多20%，D通道每分钟通过的人数比B通道每分钟通过的人数少20%，求七年级全部学生进校所需时间是多少分钟？
【考点】一元一次方程的应用．
【专题】一次方程（组）及应用；应用意识．
【分析】①设B通道每分钟通过的人数是x人，A通道每分钟通过的人数是2x人，由“八年级学生进校时同时开通了A、B两通道，经过6分钟”，列出方程可求解；
②设七年级全部学生进校所需时间是y分钟，由七年级的人数为620人，列出方程可求解．
【解答】解：①设B通道每分钟通过的人数是x人，A通道每分钟通过的人数是2x人，
由题意可得：6×（2x+x）＝450，
解得：x＝25，
∴2x＝50，
答：B通道每分钟通过的人数是25人，A通道每分钟通过的人数是50人；
②设七年级全部学生进校所需时间是y分钟，
由题意可得：（1.2×50+25+50+0.8×25）×y＝620，
解得：y＝4，
答：七年级全部学生进校所需时间是4分钟．
【点评】本题考查了一元一次方程的应用，找到正确的数量关系，列出方程是解题的关键．
21．（2021•罗湖区校级模拟）如图，已知数轴上原点为O，点B表示的数为﹣2，A在B的右边，且A与B的距离是5，动点P从点B出发，以每秒3个单位长度的速度沿数轴向右匀速运动，动点Q从点A出发，以每秒4个单位长度的速度沿数轴向左匀速运动，若点P、Q同时出发，设运动时间为t（t＞0）秒．

（1）写出数轴上点A表示的数　3　，点P表示的数　（3t﹣2）　（用含t的代数式表示），点Q表示的数　（﹣4t+3）　（用含t的代数式表示）；
（2）问点P与点Q何时到点O距离相等？
（3）若点D是数轴上一点，点D表示的数是x，是否存在x，使得|x﹣3|+|x+2|＝7？如果存在，直接写出x的值：如果不存在，说明理由．
【考点】数轴；绝对值；列代数式；一元一次方程的应用．
【专题】方程思想；一次方程（组）及应用；应用意识．
【分析】（1）由AB的长结合点A所在的位置可得出点A表示的数，由点P，Q的出发点、速度及运动时间，可用含t的代数式表示出点P，Q表示的数；
（2）由点P与点Q到点O距离相等，即可得出关于t的含绝对值符号的一元一次方程，解之即可得出结论；
（3）分x＜﹣2，﹣2≤x≤3及x＞3三种情况，解方程即可得出结论．
【解答】解：（1）∵AB＝5，且点A在点O的右侧，
∴点A表示的数为3．
∵动点P从点B出发，以每秒3个单位长度的速度沿数轴向右匀速运动，动点Q从点A出发，以每秒4个单位长度的速度沿数轴向左匀速运动，
∴点P表示的数为（3t﹣2），点Q表示的数为（﹣4t+3）．
故答案为：3；（3t﹣2）；（﹣4t+3）．
（2）依题意，得：|3t﹣2|＝|﹣4t+3|，
即3t﹣2＝﹣4t+3或3t﹣2＝4t﹣3，
解得：t＝或t＝1．
答：当t＝秒或1秒时，点P与点Q到点O距离相等．
（3）当x＜﹣2时，|x﹣3|+|x+2|＝7，即3﹣x﹣x﹣2＝7，
解得：x＝﹣3；
当﹣2≤x≤3时，|x﹣3|+|x+2|＝7，即3﹣x+x+2＝5≠7；
当x＞3时，|x﹣3|+|x+2|＝7，即x﹣3+x+2＝7，
解得：x＝4．
答：存在x＝﹣3或x＝4，使得|x﹣3|+|x+2|＝7．
【点评】本题考查了一元一次方程的应用以及列代数式，解题的关键是：（1）根据路程＝速度×时间，用含t的代数式表示出点P，Q表示的数；（2）找准等量关系，正确列出一元一次方程；（3）分x＜﹣2，﹣2≤x≤3及x＞3三种情况解方程．
22．（2020秋•龙华区期末）定义：在数轴上，如果两个数所对应点位于某点的两侧，且与这点的距离相等，我们称其中一个数与另一个数关于这点互为对称数，例如，如图，数1在数轴上所对应点为点A，则数4与数﹣2关于点A互为对称数；已知点P是数轴上一动点，数﹣1与﹣4关于点P互为对称数分别为m、n，数m与数n在数轴上对应的点分别为点M、N．
（1）当点P运动至原点O时，m＝　1　，n＝　4　；
（2）若点P运动至与点A时，m＝　3　，n＝　6　；
（3）若点P运动至与数t所对应的点时，m＝　2t+1　，n＝　2t+4　；（用含t的代数式表示）
（4）在（3）中，数t＝　2或﹣2.5或﹣7　时，点P、M，N三点中恰有一点是另两点连线段的中点．

【考点】数轴；列代数式；一元一次方程的应用．
【专题】几何动点问题；应用意识．
【分析】（1）根据互为对称数的定义，由对称中心为0即可求解；
（2）根据互为对称数的定义，由对称中心为1即可求解；
（3）根据互为对称数的定义，由对称中心为t即可求解；
（4）分三种情况，根据点P、M，N三点中恰有一点是另两点连线段的中点，列出方程计算即可求解．
【解答】解：（1）当点P运动至原点O时，m＝1，n＝4．
故答案为：1，4；
（2）若点P运动至与点A时，m＝1+（1+1）＝3，n＝1+（1+4）＝6．
故答案为：3，6；
（3）若点P运动至与数t所对应的点时，m＝2t﹣1，n＝2t+4．
故答案为：2t﹣1，2t+4；
（4）依题意有：
①2（2t+1）＝t+2t+4，
解得t＝2；
②2t＝2t+1+2t+4，
解得t＝﹣2.5；
③2（2t+4）＝t+2t+1，
解得t＝﹣7．
故在（3）中，数t＝2或﹣2.5或﹣7时，点P、M，N三点中恰有一点是另两点连线段的中点．
故答案为：2或﹣2.5或﹣7．
【点评】此题主要考查了数轴，互为对称数，一元一次方程的应用，关键是首先弄清题意，找到合适的等量关系，设出未知数，列出方程．

考点卡片
1．数轴
（1）数轴的概念：规定了原点、正方向、单位长度的直线叫做数轴．
数轴的三要素：原点，单位长度，正方向．
（2）数轴上的点：所有的有理数都可以用数轴上的点表示，但数轴上的点不都表示有理数．（一般取右方向为正方向，数轴上的点对应任意实数，包括无理数．）
（3）用数轴比较大小：一般来说，当数轴方向朝右时，右边的数总比左边的数大．
2．绝对值
（1）概念：数轴上某个数与原点的距离叫做这个数的绝对值．
①互为相反数的两个数绝对值相等；
②绝对值等于一个正数的数有两个，绝对值等于0的数有一个，没有绝对值等于负数的数．
③有理数的绝对值都是非负数．
（2）如果用字母a表示有理数，则数a 绝对值要由字母a本身的取值来确定：
①当a是正有理数时，a的绝对值是它本身a；
②当a是负有理数时，a的绝对值是它的相反数﹣a；
③当a是零时，a的绝对值是零．
即|a|＝{a（a＞0）0（a＝0）﹣a（a＜0）
3．非负数的性质：绝对值
在实数范围内，任意一个数的绝对值都是非负数，当几个数或式的绝对值相加和为0时，则其中的每一项都必须等于0．
根据上述的性质可列出方程求出未知数的值．
4．有理数的乘方
（1）有理数乘方的定义：求n个相同因数积的运算，叫做乘方．
乘方的结果叫做幂，在an中，a叫做底数，n叫做指数．an读作a的n次方．（将an看作是a的n次方的结果时，也可以读作a的n次幂．）
（2）乘方的法则：正数的任何次幂都是正数；负数的奇次幂是负数，负数的偶次幂是正数；0的任何正整数次幂都是0．
（3）方法指引：
①有理数的乘方运算与有理数的加减乘除运算一样，首先要确定幂的符号，然后再计算幂的绝对值；
②由于乘方运算比乘除运算又高一级，所以有加减乘除和乘方运算，应先算乘方，再做乘除，最后做加减．

5．非负数的性质：偶次方
偶次方具有非负性．
任意一个数的偶次方都是非负数，当几个数或式的偶次方相加和为0时，则其中的每一项都必须等于0．
6．有理数的混合运算
（1）有理数混合运算顺序：先算乘方，再算乘除，最后算加减；同级运算，应按从左到右的顺序进行计算；如果有括号，要先做括号内的运算．
（2）进行有理数的混合运算时，注意各个运算律的运用，使运算过程得到简化．
【规律方法】有理数混合运算的四种运算技巧
1．转化法：一是将除法转化为乘法，二是将乘方转化为乘法，三是在乘除混合运算中，通常将小数转化为分数进行约分计算．
2．凑整法：在加减混合运算中，通常将和为零的两个数，分母相同的两个数，和为整数的两个数，乘积为整数的两个数分别结合为一组求解．
3．分拆法：先将带分数分拆成一个整数与一个真分数的和的形式，然后进行计算．
4．巧用运算律：在计算中巧妙运用加法运算律或乘法运算律往往使计算更简便．
7．列代数式
（1）定义：把问题中与数量有关的词语，用含有数字、字母和运算符号的式子表示出来，就是列代数式．
（2）列代数式五点注意：①仔细辨别词义． 列代数式时，要先认真审题，抓住关键词语，仔细辩析词义．如“除”与“除以”，“平方的差（或平方差）”与“差的平方”的词义区分． ②分清数量关系．要正确列代数式，只有分清数量之间的关系． ③注意运算顺序．列代数式时，一般应在语言叙述的数量关系中，先读的先写，不同级运算的语言，且又要体现出先低级运算，要把代数式中代表低级运算的这部分括起来．④规范书写格式．列代数时要按要求规范地书写．像数字与字母、字母与字母相乘可省略乘号不写，数与数相乘必须写乘号；除法可写成分数形式，带分数与字母相乘需把代分数化为假分数，书写单位名称什么时不加括号，什么时要加括号．注意代数式括号的适当运用． ⑤正确进行代换．列代数式时，有时需将题中的字母代入公式，这就要求正确进行代换．

【规律方法】列代数式应该注意的四个问题
1．在同一个式子或具体问题中，每一个字母只能代表一个量．
2．要注意书写的规范性．用字母表示数以后，在含有字母与数字的乘法中，通常将“×”简写作“•”或者省略不写．
3．在数和表示数的字母乘积中，一般把数写在字母的前面，这个数若是带分数要把它化成假分数．
4．含有字母的除法，一般不用“÷”（除号），而是写成分数的形式．
8．代数式求值
（1）代数式的值：用数值代替代数式里的字母，计算后所得的结果叫做代数式的值．
（2）代数式的求值：求代数式的值可以直接代入、计算．如果给出的代数式可以化简，要先化简再求值．
题型简单总结以下三种：
①已知条件不化简，所给代数式化简；
②已知条件化简，所给代数式不化简；
③已知条件和所给代数式都要化简．
9．同类项
（1）定义：所含字母相同，并且相同字母的指数也相同，这样的项叫做同类项．
同类项中所含字母可以看成是数字、单项式、多项式等．
（2）注意事项：
①一是所含字母相同，二是相同字母的指数也相同，两者缺一不可；
②同类项与系数的大小无关；
③同类项与它们所含的字母顺序无关；
④所有常数项都是同类项．
10．整式的加减
（1）几个整式相加减，通常用括号把每一个整式括起来，再用加减号连接；然后去括号、合并同类项．
（2）整式的加减实质上就是合并同类项．
（3）整式加减的应用：
①认真审题，弄清已知和未知的关系；
②根据题意列出算式；
③计算结果，根据结果解答实际问题．
【规律方法】整式的加减步骤及注意问题
1．整式的加减的实质就是去括号、合并同类项．一般步骤是：先去括号，然后合并同类项．
2．去括号时，要注意两个方面：一是括号外的数字因数要乘括号内的每一项；二是当括号外是“﹣”时，去括号后括号内的各项都要改变符号．
11．整式的加减—化简求值
给出整式中字母的值，求整式的值的问题，一般要先化简，再把给定字母的值代入计算，得出整式的值，不能把数值直接代入整式中计算．
12．一元一次方程的解
定义：使一元一次方程左右两边相等的未知数的值叫做一元一次方程的解．
把方程的解代入原方程，等式左右两边相等．
13．解一元一次方程
（1）解一元一次方程的一般步骤：
去分母、去括号、移项、合并同类项、系数化为1，这仅是解一元一次方程的一般步骤，针对方程的特点，灵活应用，各种步骤都是为使方程逐渐向x＝a形式转化．
（2）解一元一次方程时先观察方程的形式和特点，若有分母一般先去分母；若既有分母又有括号，且括号外的项在乘括号内各项后能消去分母，就先去括号．
（3）在解类似于“ax+bx＝c”的方程时，将方程左边，按合并同类项的方法并为一项即（a+b）x＝c．使方程逐渐转化为ax＝b的最简形式体现化归思想．将ax＝b系数化为1时，要准确计算，一弄清求x时，方程两边除以的是a还是b，尤其a为分数时；二要准确判断符号，a、b同号x为正，a、b异号x为负．
14．一元一次方程的应用
（一）一元一次方程解应用题的类型有：
（1）探索规律型问题；
（2）数字问题；
（3）销售问题（利润＝售价﹣进价，利润率＝×100%）；（4）工程问题（①工作量＝人均效率×人数×时间；②如果一件工作分几个阶段完成，那么各阶段的工作量的和＝工作总量）；
（5）行程问题（路程＝速度×时间）；
（6）等值变换问题；
（7）和，差，倍，分问题；
（8）分配问题；
（9）比赛积分问题；
（10）水流航行问题（顺水速度＝静水速度+水流速度；逆水速度＝静水速度﹣水流速度）．
（二）利用方程解决实际问题的基本思路如下：首先审题找出题中的未知量和所有的已知量，直接设要求的未知量或间接设一关键的未知量为x，然后用含x的式子表示相关的量，找出之间的相等关系列方程、求解、作答，即设、列、解、答．
列一元一次方程解应用题的五个步骤
1．审：仔细审题，确定已知量和未知量，找出它们之间的等量关系．
2．设：设未知数（x），根据实际情况，可设直接未知数（问什么设什么），也可设间接未知数．
3．列：根据等量关系列出方程．
4．解：解方程，求得未知数的值．
5．答：检验未知数的值是否正确，是否符合题意，完整地写出答句．
15．直线、射线、线段
（1）直线、射线、线段的表示方法
①直线：用一个小写字母表示，如：直线l，或用两个大写字母（直线上的）表示，如直线AB．
②射线：是直线的一部分，用一个小写字母表示，如：射线l；用两个大写字母表示，端点在前，如：射线OA．注意：用两个字母表示时，端点的字母放在前边．
③线段：线段是直线的一部分，用一个小写字母表示，如线段a；用两个表示端点的字母表示，如：线段AB（或线段BA）．

（2）点与直线的位置关系：①点经过直线，说明点在直线上；②点不经过直线，说明点在直线外．
16．直线的性质：两点确定一条直线
（1）直线公理：经过两点有且只有一条直线．
简称：两点确定一条直线．
（2）经过一点的直线有无数条，过两点就唯一确定，过三点就不一定了．
17．线段的性质：两点之间线段最短
线段公理
两点的所有连线中，可以有无数种连法，如折线、曲线、线段等，这些所有的线中，线段最短．
简单说成：两点之间，线段最短．
18．两点间的距离
（1）两点间的距离
连接两点间的线段的长度叫两点间的距离．
（2）平面上任意两点间都有一定距离，它指的是连接这两点的线段的长度，学习此概念时，注意强调最后的两个字“长度”，也就是说，它是一个量，有大小，区别于线段，线段是图形．线段的长度才是两点的距离．可以说画线段，但不能说画距离．
19．角的概念
（1）角的定义：有公共端点是两条射线组成的图形叫做角，其中这个公共端点是角的顶点，这两条射线是角的两条边．
（2）角的表示方法：角可以用一个大写字母表示，也可以用三个大写字母表示．其中顶点字母要写在中间，唯有在顶点处只有一个角的情况，才可用顶点处的一个字母来记这个角，否则分不清这个字母究竟表示哪个角．角还可以用一个希腊字母（如∠α，∠β，∠γ、…）表示，或用阿拉伯数字（∠1，∠2…）表示．
（3）平角、周角：角也可以看作是由一条射线绕它的端点旋转而形成的图形，当始边与终边成一条直线时形成平角，当始 边与终边旋转重合时，形成周角．
（4）角的度量：度、分、秒是常用的角的度量单位．1度＝60分，即1°＝60′，1分＝60秒，即1′＝60″．
20．度分秒的换算
（1）度、分、秒是常用的角的度量单位．1度＝60分，即1°＝60′，1分＝60秒，即1′＝60″．
（2）具体换算可类比时钟上的时、分、秒来说明角的度量单位度、分、秒之间也是60进制，将高级单位化为低级单位时，乘以60，反之，将低级单位转化为高级单位时除以60．同时，在进行度、分、秒的运算时也应注意借位和进位的方法．
21．角平分线的定义
（1）角平分线的定义
从一个角的顶点出发，把这个角分成相等的两个角的射线叫做这个角的平分线．
（2）性质：若OC是∠AOB的平分线
则∠AOC＝∠BOC＝∠AOB或∠AOB＝2∠AOC＝2∠BOC．

（3）平分角的方法有很多，如度量法、折叠法、尺规作图法等，要注意积累，多动手实践．
22．角的计算
（1）角的和差倍分
①∠AOB是∠AOC和∠BOC的和，记作：∠AOB＝∠AOC+∠BOC．∠AOC是∠AOB和∠BOC的差，记作：∠AOC＝∠AOB﹣∠BOC．②若射线OC是∠AOB的三等分线，则∠AOB＝3∠BOC或∠BOC＝∠AOB．
（2）度、分、秒的加减运算．在进行度分秒的加减时，要将度与度，分与分，秒与秒相加减，分秒相加，逢60要进位，相减时，要借1化60．
（3）度、分、秒的乘除运算．①乘法：度、分、秒分别相乘，结果逢60要进位．②除法：度、分、秒分别去除，把每一次的余数化作下一级单位进一步去除．
23．对顶角、邻补角
（1）对顶角：有一个公共顶点，并且一个角的两边分别是另一个角的两边的反向延长线，具有这种位置关系的两个角，互为对顶角．
（2）邻补角：只有一条公共边，它们的另一边互为反向延长线，具有这种关系的两个角，互为邻补角．
（3）对顶角的性质：对顶角相等．
（4）邻补角的性质：邻补角互补，即和为180°．
（5）邻补角、对顶角成对出现，在相交直线中，一个角的邻补角有两个．邻补角、对顶角都是相对与两个角而言，是指的两个角的一种位置关系．它们都是在两直线相交的前提下形成的．
24．垂线
（1）垂线的定义
当两条直线相交所成的四个角中，有一个角是直角时，就说这两条直线互相垂直，其中一条直线叫做另一条直线的垂线，它们的交点叫做垂足．
（2）垂线的性质
在平面内，过一点有且只有一条直线与已知直线垂直．
注意：“有且只有”中，“有”指“存在”，“只有”指“唯一”
“过一点”的点在直线上或直线外都可以．
25．多边形的对角线
（1）多边形的对角线：连接多边形不相邻的两个顶点的线段，叫做多边形的对角线．
（2）n边形从一个顶点出发可引出（n﹣3）条对角线．从n个顶点出发引出（n﹣3）条，而每条重复一次，所以n边形对角线的总条数为：n（n﹣3）2（n≥3，且n为整数）
（3）对多边形对角线条数公：n（n﹣3）2的理解：n边形的一个顶点不能与它本身及左右两个邻点相连成对角线，故可连出（n﹣3）条．共有n个顶点，应为n（n﹣3）条，这样算出的数，正好多出了一倍，所以再除以2．
（4）利用以上公式，求对角线条数时，直接代入边数n的值计算，而计算边数时，需利用方程思想，解方程求n．
26．简单组合体的三视图
（1）画简单组合体的三视图要循序渐进，通过仔细观察和想象，再画它的三视图．
（2）视图中每一个闭合的线框都表示物体上的一个平面，而相连的两个闭合线框常不在一个平面上．
（3）画物体的三视图的口诀为：
主、俯：长对正；
主、左：高平齐；
俯、左：宽相等．
27．由三视图判断几何体
（1）由三视图想象几何体的形状，首先，应分别根据主视图、俯视图和左视图想象几何体的前面、上面和左侧面的形状，然后综合起来考虑整体形状．
（2）由物体的三视图想象几何体的形状是有一定难度的，可以从以下途径进行分析：
①根据主视图、俯视图和左视图想象几何体的前面、上面和左侧面的形状，以及几何体的长、宽、高；
②从实线和虚线想象几何体看得见部分和看不见部分的轮廓线；
③熟记一些简单的几何体的三视图对复杂几何体的想象会有帮助；
④利用由三视图画几何体与有几何体画三视图的互逆过程，反复练习，不断总结方法．