6.高一数学（人教B版）诱导公式（第一课时）-1教案

教学基本信息

课题

诱导公式（第一课时）

学科

数学

学段：高中

年级

高一

教材

书名：普通高中教科书 数学（B版） 必修 第三册

出版社：人民教育出版社            出版日期：  2019年 7月

教学目标及教学重点、难点

教学目标：

1. 掌握角与（），，的三角函数值之间的关系.

2. 体验借助一个角的终边与单位圆的交点的横、纵坐标分别为它的余弦、正弦值，探寻终边重合的角，终边关于坐标轴对称的角和终边关于原点对称的角的正弦、余弦值之间的关系的一般过程.

3. 利用同角三角函数关系式及终边重合的角，终边关于坐标轴对称的角和终边关于原点对称的角的正、余弦值的关系，得到正切值的关系.

教学重点：

角与（），，的三角函数值之间的关系

教学难点：

角与（），，的三角函数值之间的关系的生成过程

教学过程(表格描述)

教学环节

主要教学活动

设置意图

引入

1.  复习之前的学习成果

a. 将角的概念推广到任意角

b. 借助平面直角坐标系定义了任意角三角函数

   ，，（）

c. 借助单位圆，实现了正弦、余弦的直观表达

  ：角与单位圆交点的纵坐标

  ：角与单位圆交点的横坐标

d. 利用单位圆得到同角三角函数关系式

   （1）

   （2）（，）

整理学习成果

突出强调：

1. 正弦、余弦

的直观表达

2. 正切值等于

正弦与余弦

的比值

  为生成诱导公式

作知识铺垫

情境

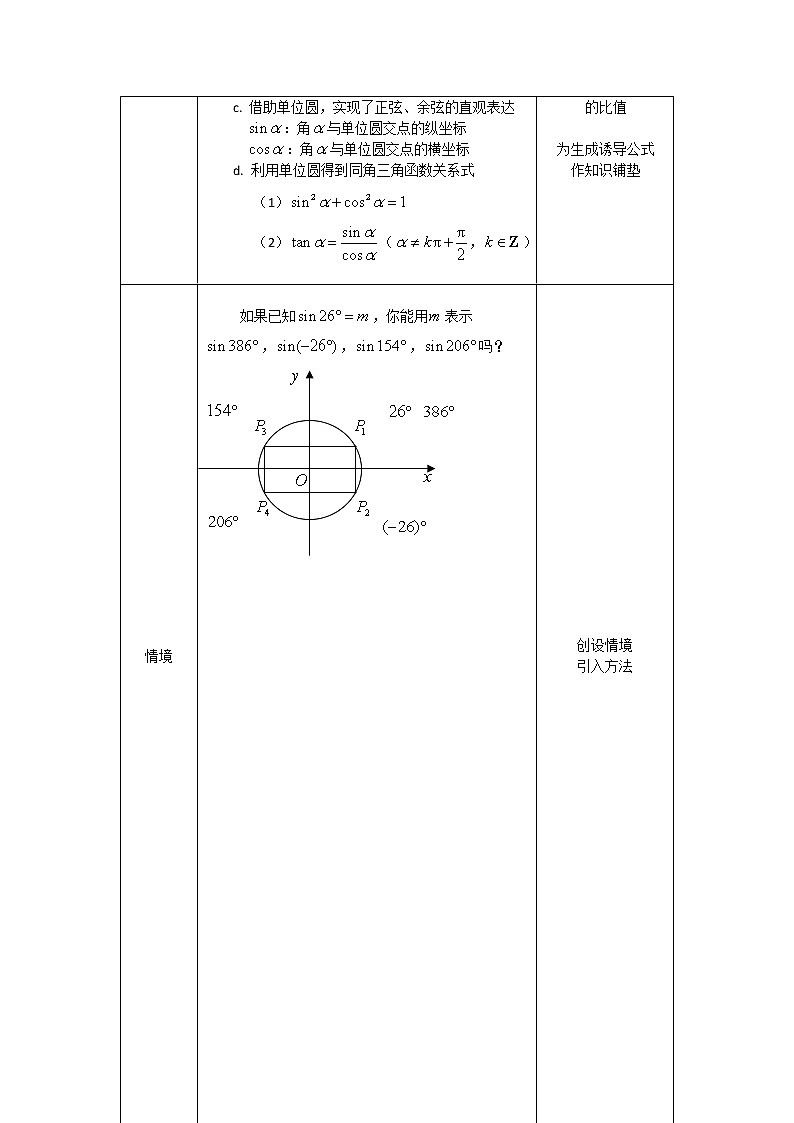
如果已知，你能用表示，，，吗？ 

创设情境

引入方法

诱导公式1

类比等式：

你能得到哪些新的结论？

（1）

（2），其中

（3）

从特殊到一般

生成

角

（其中）

的诱导公式

例题1

例1：求下列各值

（1）（2）（3）

解： （1）

     （2）

     （3）

熟悉诱导公式1

体会将绝对值

较大的角的

三角函数值向

绝对值较小的角

的三角函数值

转化的思想

诱导公式2

类比等式：

你能得到哪些新的结论？

（1）

（2）

（3）

从特殊到一般

生成角

的诱导公式

例题2

例2：求下列各值

（1）    （2）

（3）    （4）

解： （1）

     （2）

（3）

（4）

熟悉诱导公式2

体会将负角的

三角函数值向

相应的正角的

三角函数值

转化的思想

诱导公式3

类比等式：

你能得到哪些新的结论？

（1）

（2）

（3）

从特殊到一般

生成角

的诱导公式

诱导公式4

类比等式：

你能得到哪些新的结论？

（1）

（2）

（3）

从特殊到一般

生成角

的诱导公式

例题3

例3：求下列各值

（1）（2）（3）

解： （1）

     （2）

     （3）

熟悉诱导公式3

体会利用诱导

公式3将钝角

的三角函数值

向相应的锐角

三角函数值

转化的思想

例题4

例4：求下列各值

（1）（2）（3）

解： （1）

     （2）

     （3）

熟悉诱导公式4

体会利用诱导

公式4将终边

位于第三象限

的三角函数值

向相应的锐角

三角函数值

转化的思想

总结

总结提升

画龙点睛

基础性

作业

求下列各值：

（1） （2）  （3）

（4） （5）  （6）

（7）   （8）    （9）

（10）  （11）  （12）

参考答案

（1） 

（2）

（3） 

（4）

（5）

（6）

（7） 

（8）  （9）

（10）  （11）

（12）

熟悉公式

根据题目选择

恰当的

诱导公式解题

发展性

作业

 1. 对任意的，角和的终边

有何关系？

2. 对任意的，角和的三角

函数值有何关系？

体会首先关注

角的关系

再探究三角

函数值的关系

的思维方式