18.高一数学（人教B版）-向量数量积的概念(第一课时)-1教案

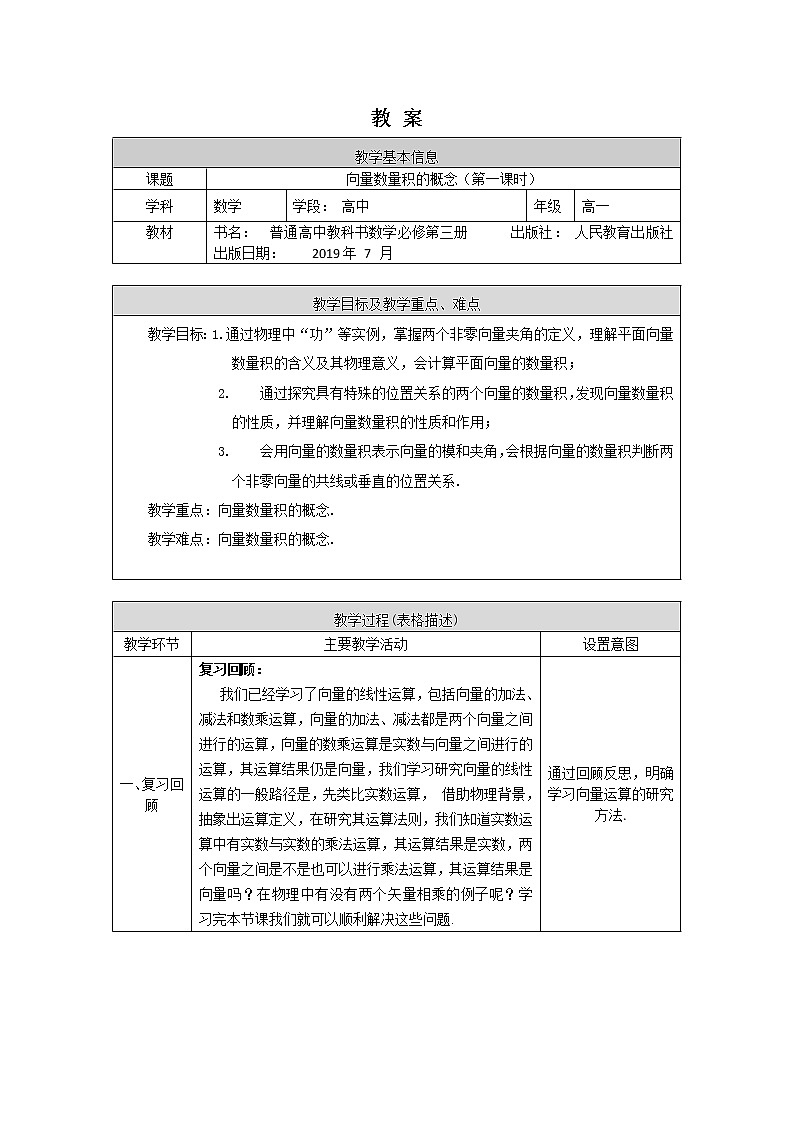
教学基本信息

课题

向量数量积的概念（第一课时）

学科

数学

学段： 高中

年级

高一

教材

书名：  普通高中教科书数学必修第三册      出版社： 人民教育出版社    出版日期：    2019年 7 月

教学目标及教学重点、难点

教学目标：1.通过物理中“功”等实例，掌握两个非零向量夹角的定义，理解平面向量数量积的含义及其物理意义，会计算平面向量的数量积；

2. 通过探究具有特殊的位置关系的两个向量的数量积，发现向量数量积的性质，并理解向量数量积的性质和作用；
3. 会用向量的数量积表示向量的模和夹角，会根据向量的数量积判断两个非零向量的共线或垂直的位置关系.

教学重点：向量数量积的概念.

教学难点：向量数量积的概念.

教学过程(表格描述)

教学环节

主要教学活动

设置意图

一、复习回顾

复习回顾：   

我们已经学习了向量的线性运算，包括向量的加法、减法和数乘运算，向量的加法、减法都是两个向量之间进行的运算，向量的数乘运算是实数与向量之间进行的运算，其运算结果仍是向量，我们学习研究向量的线性运算的一般路径是，先类比实数运算， 借助物理背景，抽象出运算定义，在研究其运算法则，我们知道实数运算中有实数与实数的乘法运算，其运算结果是实数，两个向量之间是不是也可以进行乘法运算，其运算结果是向量吗？在物理中有没有两个矢量相乘的例子呢？学习完本节课我们就可以顺利解决这些问题.

通过回顾反思，明确学习向量运算的研究方法.

二、借助物理背景、定义向量的夹角和数量积

物理情境：

    我们在物理课中学习过，物体受到力的作用，并在力的作用方向上发生了一段位移，我们就说这个力对物体做了功.如图1，设作用在小车上的力，小车在水平面上位移的大小为，如果力的方向与位移的方向相同，那么功的大小就等于力的大小与位移大小的乘积，即.如图2，当如果力的方向与位移的方向形角，将力分解为两个分力，与小车位移方向相同的力，且力，还有和位移方向垂直的力，由于小车在垂直方向没有位移，所以力对小车所做的功为

从功的计算公式中可以看出，功是一个标量，是由矢量力的大小、矢量力的大小以及两者方向的夹角决定，那么在平面向量中，给定任意两个向量，也能确定一个类似的标量，这个标量将是由两个向量的模长以及两个向量方向的差异决定，并且这就是我们本节课要学习的向量的运算数量积，类比功的公式，用夹角来刻画两个向量方向的差异，首先我们给出两个向量夹角的定义，由于图2中夹角是由力与位移在同一个作用点上进行描述的，所以定义两个向量夹角，需要把向量平移到同一个起点，下面给出两个向量夹角的定义.

1. 两个向量夹角的定义

定义：给定两个非零向量a和b，在平面内任选一点O ，作=a，=b，则称内的为向量a和b的夹角，记作〈a，b〉.   

               图3

根据定义我们来判断图3向量a与向量b、向量c、向量d、向量e的夹角的大小，由图3可知向量a与b方向向相同，选一点O，作，，则闭区间内的∠AOB的取值为零，则向量a与b夹角大小的为零，当然有夹角的定义可知，若向量a与b夹角大小的为零，也可判断这两个向量是方向相同.

接下来我们来判断向量a与向量c的夹角，向量a与向量c方向相反，我们作则闭区间内的∠AOC的取值为π，向量a与b夹角大小为π，当然有夹角的定义可知，若向量a与b夹角大小为π，也可判断这两个向量是方向相反；，所以当两个向量的夹角为0或π时，那么这两个向量是共线的，并且两个向量所在的直线是平行或者重合的.

再看判断向量a与向量d的夹角的大小，我们作则闭区间内的∠AOD的取值为，当然有夹角的定义可知，若向量a与d夹角大小为，也可判断这两个向量关系的是不共线，并且这两个向量所在的直线是相交的.

再看判断向量a与向量e的夹角的大小，我们作则闭区间内的∠AOE的取值为，向量a与向量e的夹角为，则称向量a与向量e垂直，记作a⊥e，所以当两个向量的夹角为与这两个向量垂直是等价的，并且这两个向量所在的直线是垂直关系.

由那么向量的夹角可以刻画向量的位置关系，进而可以刻画两个向量所在直线的几何位置关系.

在判断两个向量夹角大小时一定要注意，把两个向量平移到同一个起点；另外我们知道零向量方向是任意的，所以在讨论垂直问题时，规定零向量和任意向量垂直，由定义可知：〈a，b〉的取值范围为,并且〈a，b〉=〈b，a〉.

2. 向量数量积的定义

一般地，当a与b都是非零向量时，称为向量a与b数量积(也称为内积)，记作，读作a点乘b，即.

练习题：

 解：1.由已知可得

    2..由已知可得

    3.由已知可得

在应用向量数量积的定义进行计算时，这个定义式中出现了四个量，分别是向量的数量积、向量a的模长、向量b的模长以及向量夹角余弦值，这四个量，当我们知道其中三个，可根据此式列出未知那个量的方程，也就是知三求一。

在应用定义时，注意是由向量a的模长，向量b的模长以及两个向量夹角余弦值这三个数量的乘积得到，平面向量的数量积是两个向量之间的一种“乘法”运算，运算结果是一个数量，而不是向量，这与之前所学的向量的线性运算的结果仍是向量不同；平面向量在书写时，向量a与b之间用实心圆点“· ”连接，不能用实数的乘法运算符号“×”乘号.

那么两个非零向量的数量积是一个实数，当时，，；当时，，；当时，，.两个非零向量的数量积和功一样，可以为正数、可以为零、也可以为负数，符号由两个向量夹角决定.

借助物理背景“功”的概念，抽象出两个非零向量的夹角和数量积定义,并对向量数量积的定义式进行了讲解和应用;通过判断两个非零向量不同位置位置关系下的夹角的大小，体会向量夹角的作用.

三、向量数量积运算性质的探究

3.向量的数量积的性质

（1）

从对向量数量积符号的分析中，我们研究了具有特殊位置关系的两个非零向量的数量积，当向量a与b共线并且方向相同时，反之，当时，向量a与b夹角余弦值为1，则可以得到夹角大小为0，向量a与b共线并且方向相同；当向量a与b共线并且方向相反时，反之，当时，向量a与b夹角余弦值为-1，则可以得到夹角大小为π，向量a与b共线并且方向相反； 两个是等价的，所以两个非零向量的数量积和夹角一样也可以刻画向量的特殊的位置关系.

     特别地，当向量b=a时，即一般地，可以简写为即这个式子用来求向量的模长.

（2）≤

我们知道两个非零向量的数量积的符号是由这两个向量夹角决定，其大小也受到其夹角影响，接下来我们就探究两个非零向量的数量积的绝对值大小与这两个向量模长乘积的关系.

 设a和b都是非零向量,由向量的数量积可知

因为0≤〈a，b〉≤π，

所以1≤cos〈a，b〉≤1,

所以|cos〈a，b〉|≤1,

所以≤

性质（1）和（2）是在两个非零向量的条件下探究的，注意：当a和b至少有一个是零向量时，数量积的性质（1）和（2）还都成立.

（3）

向量的特殊位置关系中除了共线之外，还有垂直关系，接下来我们探究向量a与b垂直和其数量积的关系.

当向量a与b都是非零向量时.

当a和b至少有一个是零向量时，

  因为在讨论垂直问题时，零向量与任意一个向量垂直，所以有a⊥b.

 因为零向量模长为0，所以有a·b=0.

这是向量的第三条性质，对于任意向量都立，由此我们得到向量的数量积还可以刻画垂直这种特殊的位置关系.

通过探究具有特殊的位置关系下的两个向量的数量积，发现并推导出向量数量积的性质，了解向量数量积每条性质的作用，会用向量的数量积判断两个非零向量的共线或垂直的位置关系.

四、例题讲解

通过例题巩固学生对两个非零向量的夹角、向量数量积的定义和性质等知识的掌握.

五、课堂小结

本节课我们研究向量数量积的路径是借助物理中功的概念，抽象出了向量数量积的定义，进一步探究了其运算性质，最后进行应用；学习的具体内容有两个向量夹角的定义，其作用刻画了两个向量的位置关系，还学习了向量数量积运算的定义，这与我们之前学习线性运算不同，是由向量到实数的一种新的运算，最后根据两个向量的特殊位置关系探究了数量积的性质，并了解每条性质的作用.

总结本节课向量数量积的研究路径和研究内容.

六 、作业

对本节课所学知识进行巩固练习.