

27.高一数学人教B版三角恒等变换的应用(第二课时)1教案
展开教 案
教学基本信息 | ||||
课题 | 三角恒等变换的应用(第二课时) | |||
学科 | 数学 | 学段: 高中 | 年级 | 高一 |
教材 | 书名:普通高中教科书 数学 必修第三册 出版社:人民教育出版社 出版日期:2019 年 7月 | |||
教学目标及教学重点、难点 |
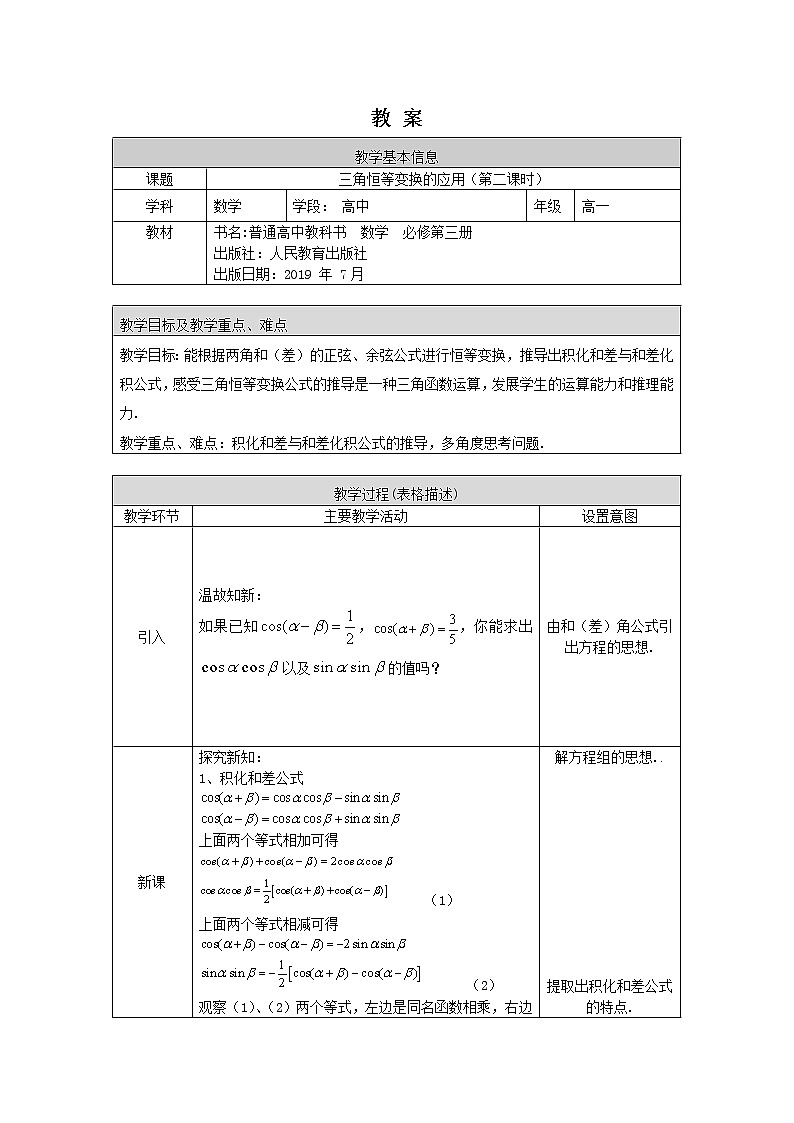
教学目标:能根据两角和(差)的正弦、余弦公式进行恒等变换,推导出积化和差与和差化积公式,感受三角恒等变换公式的推导是一种三角函数运算,发展学生的运算能力和推理能力. 教学重点、难点:积化和差与和差化积公式的推导,多角度思考问题. |
教学过程(表格描述) | ||
教学环节 | 主要教学活动 | 设置意图 |
引入 | 温故知新: 如果已知,,你能求出以及的值吗? | 由和(差)角公式引出方程的思想. |
新课 | 探究新知: 1、积化和差公式 上面两个等式相加可得 (1) 上面两个等式相减可得 (2) 观察(1)、(2)两个等式,左边是同名函数相乘,右边是两个同名函数相加或相减. 公式所起作用是将积化成和或差的形式,因此称为积化和差公式. 同样的办法: 上面两个等式相加可得 上面两个等式相减可得 小结:积化和差公式的左边是正、余弦乘积时,右边是正弦的和、差;左边是同名积时,右边是余弦的和、差. 积化和差的“和差”与“积”,是指三角函数间的关系而言,并不是指角的关系. 积化和差公式的推导用了解方程组的思想. 2、和差化积 你能借助前面所学知识求出 的最大值吗? 所以函数的最大值是1. 小结: (1).从角方面观察: 观察与恰好是与这两个角的和与差. (2).从式子结构方面观察:在化简过程中发现了与这两个角的同名三角函数积的形式,整理后为与这两个角的余弦积. 和差化积公式的推导 分析: 如果,, (换元法) 则 ,(解方程组) 两个余弦函数相加,可以写成积的形式 小结: (1).同为正弦或余弦的两个函数的和或差可以写成积的形式,因此称作和差化积.. (2).使用了换元法推导和差化积的公式. | 解方程组的思想..
提取出积化和差公式的特点.
提出和差化积的来源, 由特殊到一般的数学思想.
换元法与方程组思想的再次体现.
|
例题 | 例1 求函数的周期和最大值. 分析:我们知道只能化简成一个角的一个三角函数的一次式才可以求周期. 解:
函数的周期和最大值 例2 求函数的周期和最大值.. 分析:发现是同名三角函数的和,而且系数都是1,可以运用和差化积公式. 解:由和差化积公式可知
所以函数的周期为,最大值为. 小结:在使用积化和差、和差化积公式,应注意两个角的和或差以后往往会出现特殊角,所以“和积互化”是三角函数恒等变形的一种基本手段. 例3 求函数, 的最值. 分析:和差化积公式只对系数绝对值相等且同为正弦或余弦的和与差才能直接使用. 利用诱导公式将其中的一个化为与另一个同名的函数. 法一:
法二:
下面的任务是由 ,当即 有最大值1, 所以的最大值是2. . 法三: 法四: 因为 所以 根据正弦函数性质可知,当 即有最大值1, 所以的最大值是2. 小结:此题告诉我们化简的途径有很多,可以从式子结构入手,也可以从角之间关系入手都可以达到化简的目的. | 巩固积化和差公式.
巩固和差化积公式..
体会转化的思想.
巩固三角函数最值的求法.
和差化积公式的应用.
体会诱导公式的作用.
和(差)正余弦公式及辅助角公式的复习.
观察已知角之间的关系,使用诱导公式..
加强正弦型函数最值的求法. |
总结 |
| 梳理公式的由来. |
作业 | 1.已知,, 求,的值. 2.求下列各式的值
| 巩固本节课知识. |
27.高中数学(人教B版)-空间中的平行和垂直的综合应用(一)-1教案: 这是一份27.高中数学(人教B版)-空间中的平行和垂直的综合应用(一)-1教案,共5页。
26.高一数学(人教B版)三角恒等变换的应用(第一课时)1教案: 这是一份26.高一数学(人教B版)三角恒等变换的应用(第一课时)1教案,共5页。
人教版新课标B必修33.3.2随机数的含义与应用教学设计: 这是一份人教版新课标B必修33.3.2随机数的含义与应用教学设计,共3页。教案主要包含了〖复习回顾〗,〖新知探究〗,〖典型例题〗,〖归纳小结〗,〖板书设计〗,〖教后记〗,〖课堂作业〗等内容,欢迎下载使用。