北京市东城区2021-2022学年七年级上学期期末数学试题（word版 含答案）

这是一份北京市东城区2021-2022学年七年级上学期期末数学试题（word版 含答案），共7页。试卷主要包含了填空题，解答题解答应写出文字说明等内容，欢迎下载使用。
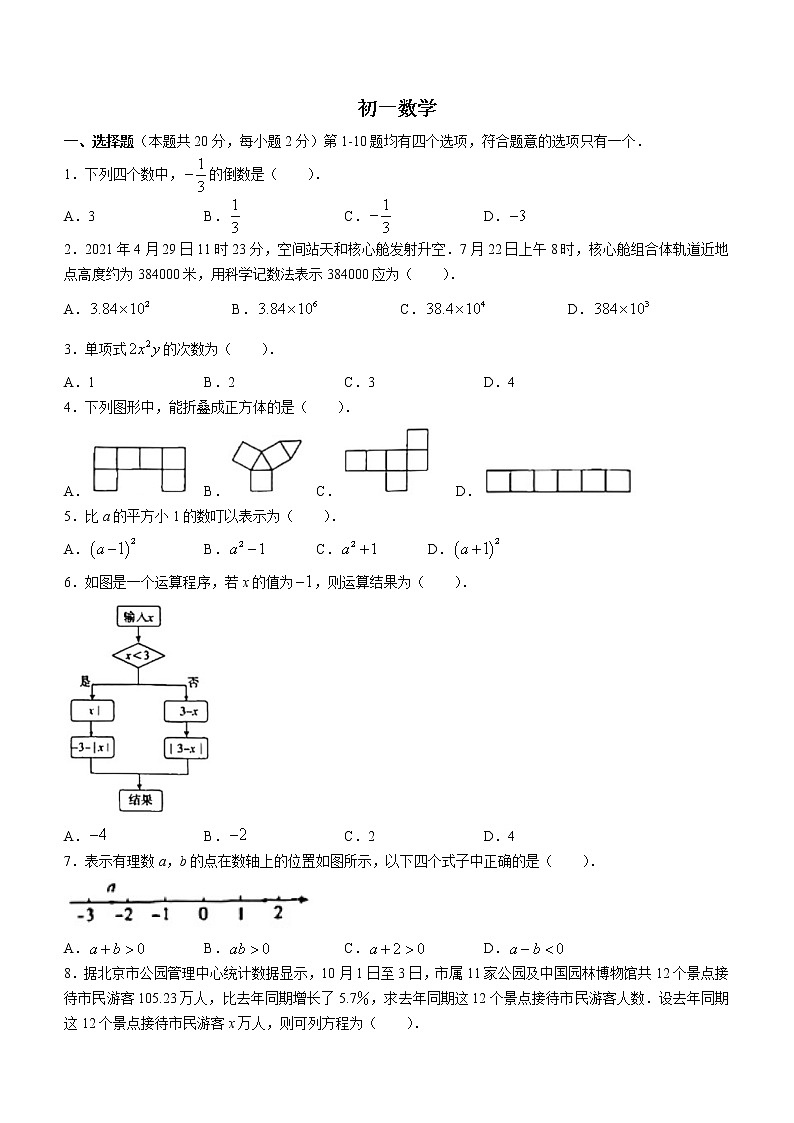
初一数学一、选择题（本题共20分，每小题2分）第1-10题均有四个选项，符合题意的选项只有一个．1．下列四个数中，的倒数是（    ）．A．3    B．    C．    D．2．2021年4月29日11时23分，空间站天和核心舱发射升空．7月22日上午8时，核心舱组合体轨道近地点高度约为384000米，用科学记数法表示384000应为（    ）．A．   B．   C．   D．3．单项式的次数为（    ）．A．1    B．2    C．3    D．44．下列图形中，能折叠成正方体的是（    ）．A． B． C． D．5．比a的平方小1的数叮以表示为（    ）．A．   B．  C．  D．6．如图是一个运算程序，若x的值为，则运算结果为（    ）．A．    B．    C．2    D．47．表示有理数a，b的点在数轴上的位置如图所示，以下四个式子中正确的是（    ）．A．   B．   C．   D．8．据北京市公园管理中心统计数据显示，10月1日至3日，市属11家公园及中国园林博物馆共12个景点接待市民游客105.23万人，比去年同期增长了5.7％，求去年同期这12个景点接待市民游客人数．设去年同期这12个景点接待市民游客x万人，则可列方程为（    ）．A．     B．C．      D．9．下列说法正确的是（    ）．A．若，则B．若，则C．若点A，B，C不在同一条直线上，则D．若，则点M为线段AB的中点10．如图所示，在长方形ABCD中，，，且，将长方形ABCD绕边AB所在的直线旋转一周形成圆柱甲，再将长方形ABCD绕边BC所在直线旋转一周形成圆柱乙，记两个圆柱的侧面积分別为、．下列结论中正确的是（    ）．A．    B．    C．   D．不确定二、填空题（本题共12分，每小题2分）11．若，，则与的关系是______．（填“互余”或“互补”）12．如图，正方体纸盒上相对两个面上的数互为相反数，则正方体纸盒六个面上的数中，最小的是______．13．若是关于x的一元一次方程，则m的值可以是______．（写出一个即可）14．已知m，n为正整数，若合并同类项后只有两项，则______，______．15．在数轴上，点A到原点O的距离为4，则线段OA的中点所表示的数为______．16．表示不超过数x的最大整数，当时，表示的整数为______；若，则______．三、解答题（本题共68分，第17题8分，第18-19题，每小题5分，第20题4分，第21题10分，第22题5分，第23题6分，第24题5分，第25题6分，第26-27题，每小题7分）解答应写出文字说明、演算步骤或证明过程．17．计算：（1）；    （2）．18．化简多项式，当，时，求该多项式的值．19．如图，A地和B地都是海上观测站，从A地发现它的东北方向（北偏东45°）有一艘船．同时，从B地发现这艘船在它的北偏西60°方向．在图中画出这艘船的位置O．（保留作图痕迹）20．若一个角的补角是它的余角的6倍，求这个角的度数．21．解方程：（1）；    （2）．22．如图，点O在直线AB上，，和互补．（1）根据已知条件，可以判断，将如下推理过程补充完整（括号内填推理依据）．推理过程：因为和互补，所以______°．（______）因为点O在直线AB上，所以．所以，所以．（______）（2）求的度数．23．在数学课上，老师展示了下列向题，请同学们分组讨论解决的方法．中国古代人民很早就在生产生活中发现了许多有趣的数学问题，其中《孙子算经》中有这样一个问题：“今有三人共车，二车空；二人共车，九人步，问人和车各几何？”这个题的意思是：今有若干人乘车．若每3人乘一辆车，则余2辆空车；若每2人乘一辆车．则余9人需步行，问共有多少辆车，多少人？某小组选择用一元一次方程解决问题，请补全他们的分析过程：第一步，设共有x辆车；第二步，由“若每3人乘一辆车，则余2辆空车”，可得人数为______；（用含x的式子表示）；第三步，由“若每2人乘一辆车，则余9人需步行”．可得人数为______（用含x的式子表示）；第四步，根据两种乘车方式的人数相等，列出方程为______．24．如图，，射线OC为的平分线．（1）画出射线OC；（2）若射线OD在的内部，且∠BOD=20°，求的度数．25．如图，点A，B，C不在同一条直线上．（l）画直线AB；（2）尺规作图：作射线CF交直线AB于点D，使得（不写作法，保留作图痕迹）．26．某工厂需将产品分别运送至不同的仓库，为节约运费，考察了甲、乙两家运输公司．甲、乙公司的收费标准如下表：运输公司起步价（单位：元）里程价（单位：元/千米）甲10005乙50010（1）仓库A距离该工厂120千米，应选择哪家运输公司？（2）仓库B，C，D与该工厂的距离分别为60千米、100千米、200千米，运送到哪个仓库时，可以从甲、乙两家运输公司任选一家？（3）根据以上信息，你能给工厂提供选择甲、乙公司的标准吗？27．对于点M，N，给出如下定义：在直线MN上，若存在点P，使得，则称点P是“点M到点N的k倍分点”．例如：如图，点，，在同一条直线上，，，则点是点到点倍分点，点是点到点的3倍分点．已知：在数轴上，点A，B，C分别表示，，2．（1）点B是点A到点C的______倍分点，点C是点B到点A的______倍分点；（2）点B到点C的3倍分点表示的数是______；（3）点D表示的数是x，线段BC上存在点A到点D的2倍分点，写出x的取值范围．东城区2021-2022学年度第一学期期末统一检测初一数学参考答案及评分标准一、选择题（本题共20分，每小题2分）题号12345678910答案DACCBADBCC二、填空题（本题共12分，每小题2分）11．互余     12．    13．1（答案不唯一）14．，  15．2或   16．5，2三、解答题（本题共68分，第17题8分，第18-19题，每小题5分，第20题4分，第21题10分，第22题5分，第23题6分，第24题5分，第25题6分，第26-27题，每小题7分）17．解：（1）．（2）．18．解：．当，时，原式．19．解：如图．20．解：设这个角为x°，则它的余角为，补角为．根据题意，列方程得，解得．答：这个角是72°．21．解：（1）移项，得．合并同类项，得．系数化为1，得．所以方程的解为．（2）去分母，得．去括号，得．移项，得．合并同类项，得．系数化为1，得．所以方程的解为．22．解：（1）推理过程：因为和互补，所以．（补角定义）因为点O在直线AB上，所以．所以．所以．（同角的补角相等） ．（2）因为，，所以．由（1）知，所以OD是的平分线．所以．23．解：某小组选择用一元一次方程解决问题，请补全他们的分析过程：第一步，设共有x辆车；第二步，由“若每3人乘一辆车，则余2 辆空车”，可得人数为（用含x的式子表示）；第三步，由“若每2人乘一辆车，则余9人需步行”，可得人数为（用含x的式子表示）；第四步，根据两种乘车方式的人数相等，列出方程为．24．解：（1）如图所示：（2）如图所示：因为OC是的平分线，且，所以．因为，所以．25．解：如图所示：26．解：（1）甲运输公司收费为（元），乙运输公司收费为（元）．因为，所以该工厂选择甲运输公司更划算．（2）设当运输距离为x千米时，甲、乙两家运输公司收费相同．根据题意，得，解得．答：运送到C仓库时，甲、乙两家运输公司收费相同，可以任选一家．（3）当仓库与工厂的距离大于100千米时，选择甲公司；当仓库与工厂的距离等于100千米时，可以从甲、乙公司中任选一家；当仓库与工厂的距离小于100千米时，选择乙公司．27．解：（1），；（2）1或4；（3）．