山东省东营市广饶县2021-2022学年八年级上学期期末考试数学试题(word版 含答案)
展开第I卷(选择题共30分)
一、选择题:本大题共10小题,在每小题给出的四个选项中,只有一项是正确的请把正确的选项选出来。每小题选对得3分,选错、不选或选出的答案超过一个均记零分
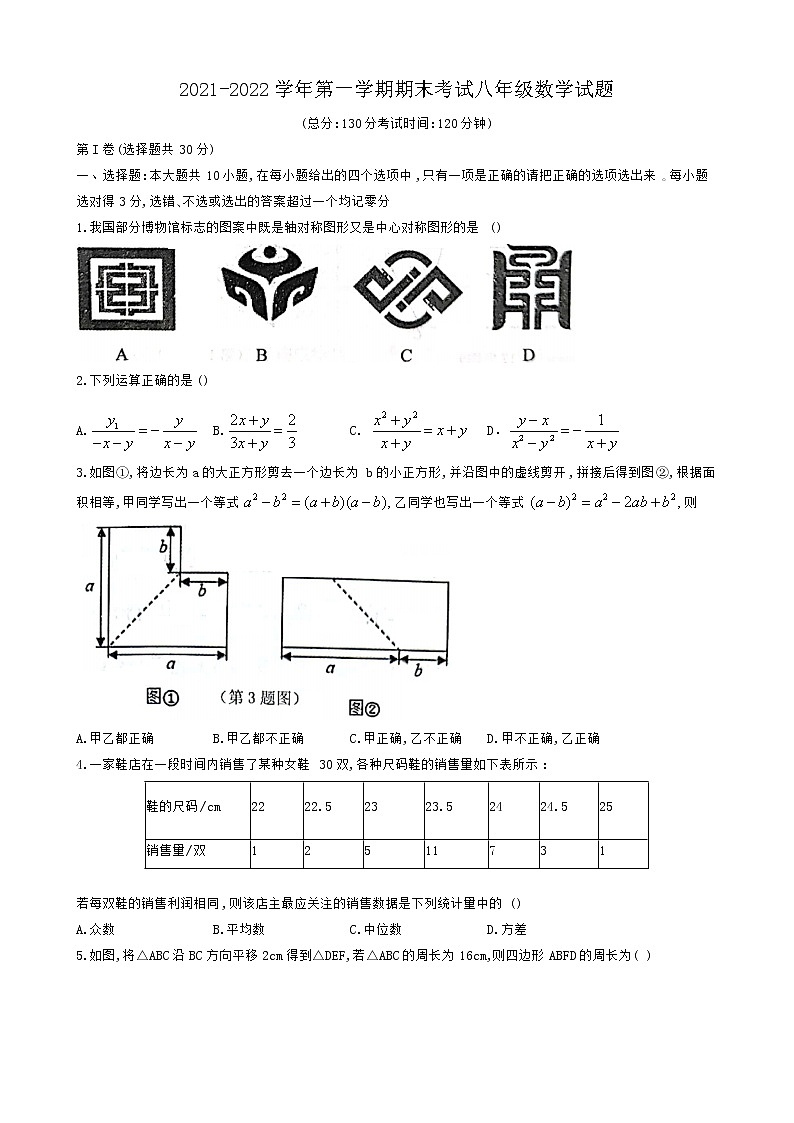
1.我国部分博物馆标志的图案中既是轴对称图形又是中心对称图形的是()
2.下列运算正确的是()
A.B.C. D.
3.如图①,将边长为a的大正方形剪去一个边长为b的小正方形,并沿图中的虚线剪开,拼接后得到图②,根据面积相等,甲同学写出一个等式乙同学也写出一个等式则
A.甲乙都正确B.甲乙都不正确C.甲正确,乙不正确D.甲不正确,乙正确
4.一家鞋店在一段时间内销售了某种女鞋30双,各种尺码鞋的销售量如下表所示:
若每双鞋的销售利润相同,则该店主最应关注的销售数据是下列统计量中的()
A.众数B.平均数C.中位数D.方差
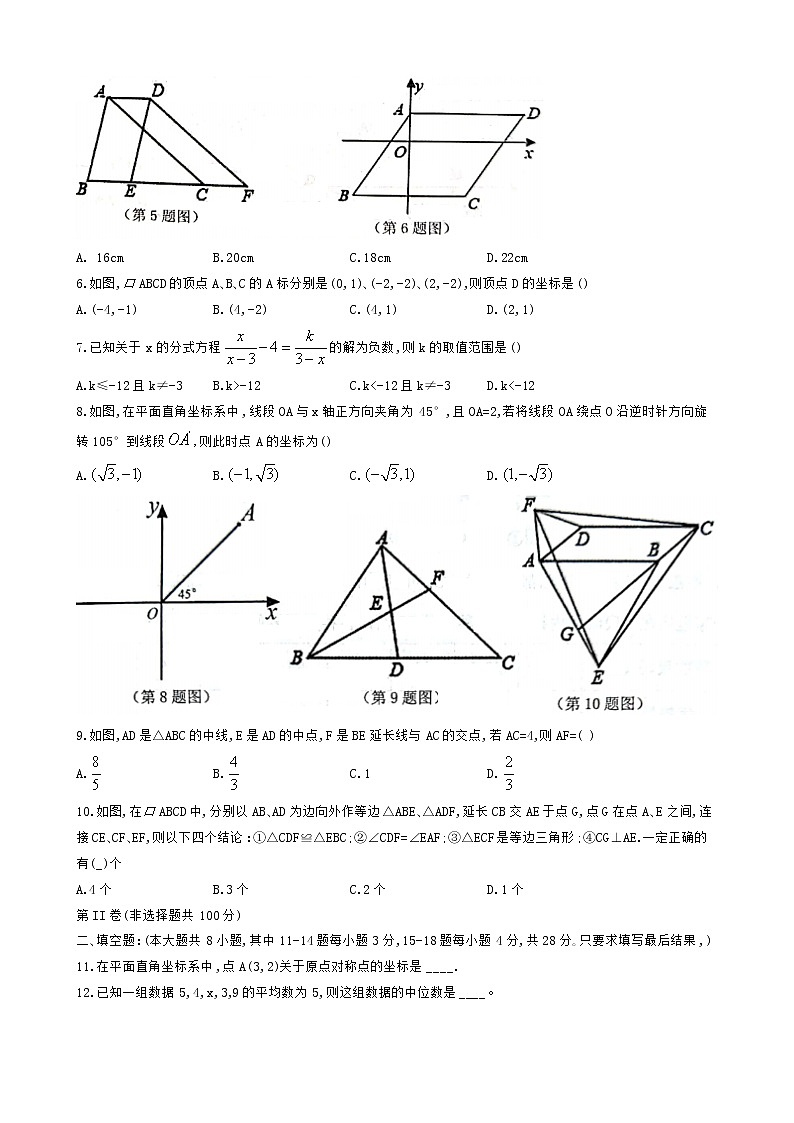
5.如图,将△ABC沿BC方向平移2cm得到△DEF,若△ABC的周长为16cm,则四边形ABFD的周长为( )
A. 16cm B.20cmC.18cmD.22cm
6.如图,口ABCD的顶点A、B、C的A标分别是(0,1)、(-2,-2)、(2,-2),则顶点D的坐标是()
A.(-4,-1)B.(4,-2)C.(4,1)D.(2,1)
7.已知关于x的分式方程的解为负数,则k的取值范围是()
A.k≤-12且k≠-3B.k>-12C.k<-12且k≠-3D.k<-12
8.如图,在平面直角坐标系中,线段OA与x轴正方向夹角为45°,且OA=2,若将线段OA绕点O沿逆时针方向旋转105°到线段则此时点A的坐标为()
A.B.C.D.
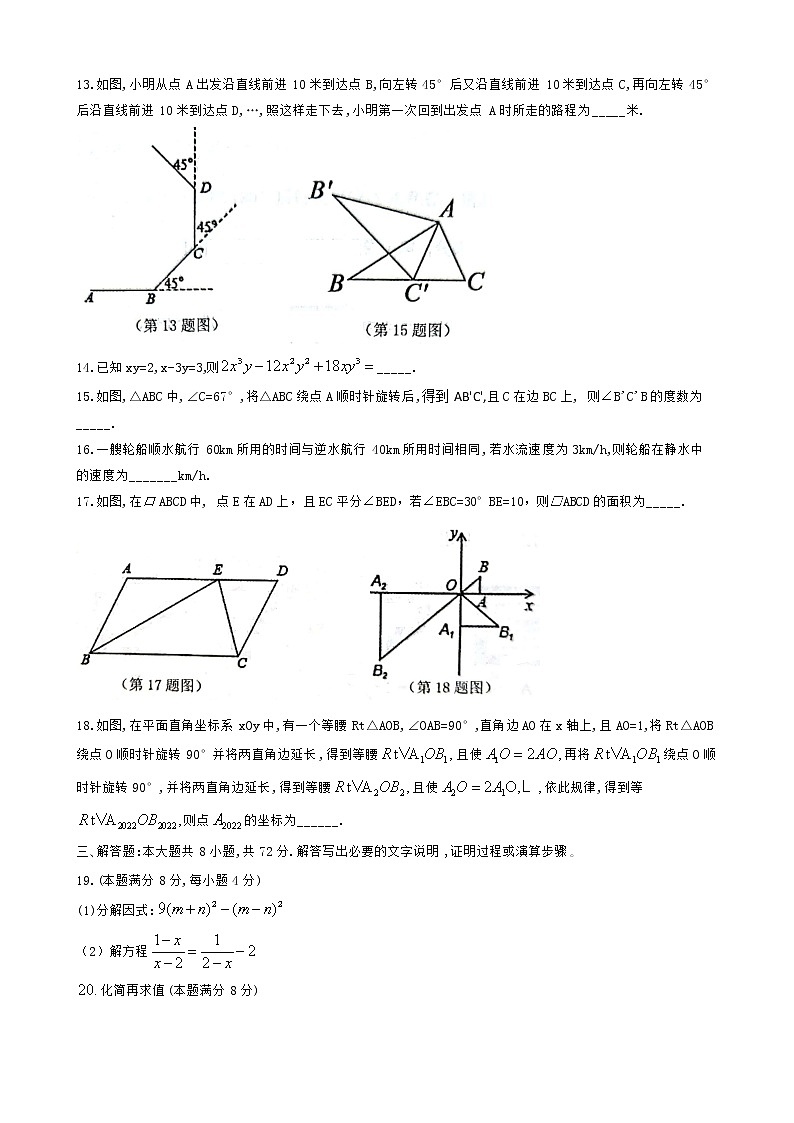
9.如图,AD是△ABC的中线,E是AD的中点,F是BE延长线与AC的交点,若AC=4,则AF=( )
A.B.C.1D.
10.如图,在口ABCD中,分别以AB、AD为边向外作等边△ABE、△ADF,延长CB交AE于点G,点G在点A、E之间,连接CE、CF、EF,则以下四个结论:①△CDF≌△EBC;②∠CDF=∠EAF;③△ECF是等边三角形;④CG⊥AE.一定正确的有(_)个
A.4个B.3个C.2个D.1个
第II卷(非选择题共100分)
二、填空题:(本大题共8小题,其中11-14题每小题3分,15-18题每小题4分,共28分。只要求填写最后结果,)
11.在平面直角坐标系中,点A(3,2)关于原点对称点的坐标是____.
12.已知一组数据5,4,x,3,9的平均数为5,则这组数据的中位数是____。
13.如图,小明从点A出发沿直线前进10米到达点B,向左转45°后又沿直线前进10米到达点C,再向左转45°后沿直线前进10米到达点D,…,照这样走下去,小明第一次回到出发点A时所走的路程为_____米.
14.已知xy=2,x-3y=3,则_____.
15.如图,△ABC中,∠C=67°,将△ABC绕点A顺时针旋转后,得到AB'C',且C在边BC上, 则∠B'C'B的度数为_____.
16.一艘轮船顺水航行60km所用的时间与逆水航行40km所用时间相同,若水流速度为3km/h,则轮船在静水中的速度为_______km/h.
17.如图,在口ABCD中, 点E在AD上,且EC平分∠BED,若∠EBC=30°BE=10,则□ABCD的面积为_____.
18.如图,在平面直角坐标系xOy中,有一个等腰Rt△AOB,∠OAB=90°,直角边AO在x轴上,且AO=1,将Rt△AOB绕点O顺时针旋转90°并将两直角边延长,得到等腰且使再将绕点O顺时针旋转90°,并将两直角边延长,得到等腰且使依此规律,得到等
则点的坐标为______.
三、解答题:本大题共8小题,共72分.解答写出必要的文字说明证明过程或演算步骤。
19.(本题满分8分,每小题4分)
(1)分解因式:
(2)解方程
化简再求值(本题满分8分)
已知,其中x是不等式组的整数解.
21.(本题满分10分)
2021年广饶县中学生篮球联赛于12月16日-18日举行,学校在全校选拔篮球队员组建篮球队,教练员为了从甲、乙两名同学中选拔一人参加校篮球队,对他们进行了8次定点投篮测试,每次投10个球,测试成绩(单位:个)如下表:
(1)根据表格中的数据,计算出甲的平均成绩是___个,乙的平均成绩是___个;
(2)分别计算甲、乙两名同学8次测试成绩的方差;
(3)根据(1)(2)计算的结果,你认为选谁参加校篮球队更合适,并说明理由.
22.(本题满分8分)
如图,在平面直角坐标系中,△ABC的三个顶点分别是A(1,3)、B(4,4)、C(2,1)。
(1)把△ABC向左平移4个单位后得到对应的△请画出平移后的△;
(2)把△ABC绕点O旋转180°后得到对应△请画出旋转后的△;
(3)观察图形,判断公与△是否成中心对称?如果是,直接写出对称中心的坐标.
23.(本题满分9分)
如图,□ABCD中,BD是它的一条对角线,过点A、C作AE⊥BD、CF⊥BD,垂足分别为E、F,延长AE、CF分别交CD、AB于点M、N.
(1)求证:四边形CMAN是平行四边形.
(2)已知DE=4,FN=3,求BN的长.
24.(本题满分9分)
2021年是中国共产党建党100周年,为深入了解党的光荣历史,东营市某中学团委组织全校共青团员到广饶刘集红色旅游区开展红色研学之旅,旅游区距学校120km部分学生乘慢车先行,出发20min后,另一部分学生乘快车前往,结果他们同时到达旅游区。已知快车的平均速度是慢车平均速度的1.2倍,求慢车的平均速度.
25.(本题满分10分)
【教材呈现】如图是鲁教版八年级上册教材第142页的第1题,请完成这道题的证明.
(1)如图①,在四边形ABCD中,AD=BC,P是对角线BD的中点,M是DC的中点,N是AB的中点,求证:∠PMN=∠PMM.
【教材延伸】
(2)如图②,延长图①中的线段AD交MM的延长线于点E,延长线段BC交MM的延长线于点F,求证:∠AEN=∠F.
【应用探究】
(3)如图③,在△ABC中,AC
已知△AOB和△MON都是等腰直角三角形(),∠AOB=∠MON=90°.
(1)如图1,连接求证:△AOM≌△BON;
(2)若将△MON绕点O顺时针旋转,
①如图2,当点N恰好在AB边上时,求证:;
②当点A、M、N在同一条直线上时,若OA=3,MN=4,请直接写出线段BN的长.
2021—2022学年第一学期期末考试
八年级数学参考答案
评卷说明:
1. 选择题和填空题中的每小题,只有满分和零分两个评分档,不给中间分.
2. 解答题中的每小题的解答中所对应的分数,是指考生正确解答到该步骤所应得的累计分数.对考生的其他解法,请参照评分意见相应评分.
3. 如果考生在解答的中间过程出现计算错误,但并没有改变试题的实质和难度,其后续部分酌情给分,但最多不超过正确解答分数的一半;若出现严重的逻辑错误,后续部分就不再给分.
一、选择题(每题3分,共30分)
二、填空题(11-14题每小题3分,15-18题每小题4分,共28分.)
11. (﹣3,﹣2) ; 12. 4 ; 13. 80 ; 14. 36 ;
15. 46°; 16. 15 ; 17. 50; 18.(-22022,0).
三、解答题
19.(本题满分8分,每小题4分)
解:(1)9(m+n)2﹣(m﹣n)2
=[3(m+n)]2﹣(m﹣n)2 …………………………………………1分
=[3(m+n)+(m﹣n)][3(m+n)﹣(m﹣n)]……………………2分
=(4m+2n)(2m+4n);…………………………………………………3分
=4(2m+n)(m+2n);…………………………………………………4分
(2)去分母得:1﹣x=﹣1﹣2x+4, ………………………………1分
解得:x=2, …………………………………………………………2分
检验:当x=2时,原分式方程分母等于0,应舍去 ………………………3分
因此,原分式方程无解.………………………………4分
20.(本题满分8分)
解:
………………………………1分
……………………………………2分
………………………………………………3分
………………………………………………………4分
由不等式组,得﹣2≤x<1.5,………………5分
又∵x取整数解,
∴x=-2,-1,0或1,………………………………………6分
∵当x=-2,-1,1时,原分式无意义,
∴x=0,………………………………………………………7分
当x=0时,原式==-1.………………………………8分
21.(本题满分10分)
解:(1)甲的平均成绩为:×(10+8+9+8+10+9+10+8)=9(环),
乙的平均成绩为:×(10+7+10+10+9+8+8+10)=9(环),
故答案为:9;9;(每空2分)……………………………………4分
(2)甲的方差为:[(10﹣9)2+(8﹣9)2+(9﹣9)2+(8﹣9)2+(10﹣9)2+(9﹣9)2+(10﹣9)2+(8﹣9)2]=0.75,………………………………6分
乙的方差为:[(10﹣9)2+(7﹣9)2+(10﹣9)2+(10﹣9)2+(9﹣9)2+(8﹣9)2+(8﹣9)2+(10﹣9)2]=1.25,……………………………………8分
(3)∵9=9,0.75<1.25,
∴甲乙平均值相等,且甲的方差小,
∴甲比较稳定,故选甲参加校篮球队更合适.………………………10分
22.(本题满分8分)
解:(1)如图,Δ即为所求;…………………………………3分
(2)如图,Δ即为所求;……………………………………6分
(3)由图得,Δ与Δ成中心对称图形,对称中心坐标为(﹣2,0).…8分
23.(本题满分9分)
(1)证明:∵四边形ABCD是平行四边形,
∴CD∥AB,………………………………………………………………1分
∵AM⊥BD,CN⊥BD,
∴AM∥CN,………………………………………………………………2分
∴CM∥AN,AM∥CN,
∴四边形AMCN是平行四边形.………………………………………4分
(2)∵四边形AMCN是平行四边形,
∴CM=AN,……………………………………………………………5分
∵四边形ABCD是平行四边形,
∴CD=AB,CD∥AB,………………………………………………6分
∴DM=BN,∠MDE=∠NBF,……………………………………7分
在△MDE和△NBF中,
,
∴△MDE≌△NBF(AAS),
∴BF=DE=3,………………………………………………………8分
在Rt△NBF中,∵∠BFN=90°,BF=4,NF=3,
∴BN===5,……………………………9分
24.(本题满分9分)
解:设慢车的速度为x km/h,则快车的速度为1.2x km/h,根据题意得
,………………………………………………………1分
﹣=,…………………………………………………4分
解得:x=60,………………………………………………………7分
经检验,x=60是原方程的根.……………………………………8分
答:慢车的平均速度是60km/h.……………………………………9分
25.(本题满分10分)
【教材呈现】
(1)证明:∵P是BD的中点,M是DC的中点,
∴PM=BC,………………………………1分
同理,PN=AD,…………………………2分
∵AD=BC,
∴PM=PN,………………………………3分
∴∠PMN=∠PNM,……………………4分
【教材延伸】
(2)证明:∵P是BD的中点,M是DC的中点,
∴PM∥BC,…………………………5分
∴∠PMN=∠F,……………………6分
同理,∠PNM=∠AEN,……………7分
∵∠PMN=∠PNM,
∴∠AEN=∠F;…………………8分
【应用探究】
(3)直角三角形.……………………………………………10分
证明:如图连接BD,取BD的中点P,连接PM、PN,
∵M是CD的中点,
∴PM∥BC,PM=BC,
同理,PN∥AD,PN=AD,
∵AD=BC
∴PM=PN,
∴∠PNM=∠PMN,
∵PN∥AD,
∴∠PNM=∠AMN=60°,
第26题图③
∴∠PNM=∠PMN=60°,
∵PM∥BC,
∴∠CGM=∠PMN=60°,
又∵∠CMG=∠AMN=60°
∴△CGM是等边三角形.
∵CM=GM,
又∵CM=DM
∴DM=GM,
∴∠MDG=∠MGD=30°
∴∠CGD=90°
即△CGD是直角三角形.
26.(本题满分10分)
(1)证明:如图1中,
∵∠AOB=∠MON=90°,
∴∠AOM=∠BON,………………………………………1分
∵AO=BO,OM=ON,………………………………………2分
∴△AOM≌△BON(SAS).…………………………………3分
(2)①证明:如图2中,连接AM.
同法可证△AOM ≌△BON,
∴AM=BN,∠OAM=∠B=45°,……………………………4分
∵∠OAB=∠B=45°,
∴∠MAN=∠OAM+∠OAB=90°,………5分
∴,……………………6分
∵△MON是等腰直角三角形,
∴,………………………7分
∴.………………………8分
②如图3﹣1中,∴BN=.…………………9分
如图3﹣2中,BN=.………………………………………10分
鞋的尺码/cm
22
22.5
23
23.5
24
24.5
25
销售量/双
1
2
5
11
7
3
1
第一次
第二次
第三次
第四次
第五次
第六次
第七次
第八次
甲
10
8
9
8
10
9
10
8
乙
10
7
10
10
9
8
8
10
1
2
3
4
5
6
7
8
9
10
A
D
C
A
B
C
D
C
B
B
山东省东营市广饶县2023-2024学年八年级上学期1月期末数学试题: 这是一份山东省东营市广饶县2023-2024学年八年级上学期1月期末数学试题,共5页。
2021-2022学年山东省东营市广饶县八年级上学期期末数学试题及答案: 这是一份2021-2022学年山东省东营市广饶县八年级上学期期末数学试题及答案,共26页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
山东省东营市广饶县2023-2024学年八年级上学期1月期末数学试题(图片版): 这是一份山东省东营市广饶县2023-2024学年八年级上学期1月期末数学试题(图片版),文件包含2023-2024学年第一学期期末考试八年级数学答案docx、山东省东营市广饶县2023-2024学年八年级上学期1月期末数学试题docx等2份试卷配套教学资源,其中试卷共11页, 欢迎下载使用。












