【备战2022】高考数学选择题专题强化训练：余弦函数的性质

展开

这是一份【备战2022】高考数学选择题专题强化训练：余弦函数的性质，共8页。试卷主要包含了选择题等内容，欢迎下载使用。

一、选择题（共29小题；共145分）
1. 下列不等式正确的是
A. sin130∘>sin40∘>lg34B. tan226∘C. cs−20∘sin80∘>lg52

2. 如果 π4<α<π2，那么下列不等式成立的是
A. csαC. sinα
3. 下列区间中，使函数 y=csx 为增函数的是
A. 0,πB. π2,3π2C. −π2,π2D. π,2π

4. 函数 y=csx，x∈−π6,π2 的值域是
A. 0,1B. −1,1C. 0,32D. −12,1

5. y=cs2x2 的最小正周期为
A. π3B. π4C. πD. 2π

6. 关于余弦函数 y=csx 的图象，有下列说法：
① 关于 y 轴对称；② 当 x=2kπ+πk∈Z 时，图象处于最低点；③ 在区间 0,π 上图象单调上升．
其中正确的有个．
A. 0B. 1C. 2D. 3

7. 下列函数中，图象关于坐标原点对称的是
A. y=lgxB. y=csxC. y=∣x∣D. y=sinx

8. 已知函数 fx=csx+π2 （ x∈R ），则下列叙述错误的是
A. fx 的最大值与最小值之和等于 π
B. fx 是偶函数
C. fx 在 4,7 上是增函数
D. fx 的图象关于点 −π2,π2 成中心对称

9. 函数 y=2csx，x∈0,2π 和 y=2 的图象围成的一个封闭的平面图形的面积是
A. 2B. 4C. 2πD. 4π

10. 如果函数 y=3cs2x＋φ 的图象关于点 4π3,0 中心对称，那么 ∣φ∣ 的最小值为
A. π6B. π4C. π3D. π2

11. 函数 fx=cssinx 的定义域是
A. 2kπ−π2,2kπ+π2 ， k∈ZB. 2kπ,2kπ+π2 ， k∈Z
C. 2kπ−π2,2kπ ， k∈ZD. R

12. 若函数 y=2csx0≤x≤2π 的图象和直线 y=2 围成一个封闭的平面图形，则这个封闭图形的面积是
A. 4B. 8C. 2πD. 4π

13. 已知 fx=asinx+bx3ccsx+3，若 f5=−2，则 f−5 等于
A. 2B. 5C. 8D. −3

14. 已知集合 A=αcsα>12，B=α0<α<π，且 A∩B=C，则 C=
A. α0<α<π6B. απ3<α<π2
C. α0<α<π3D. απ3<α<π

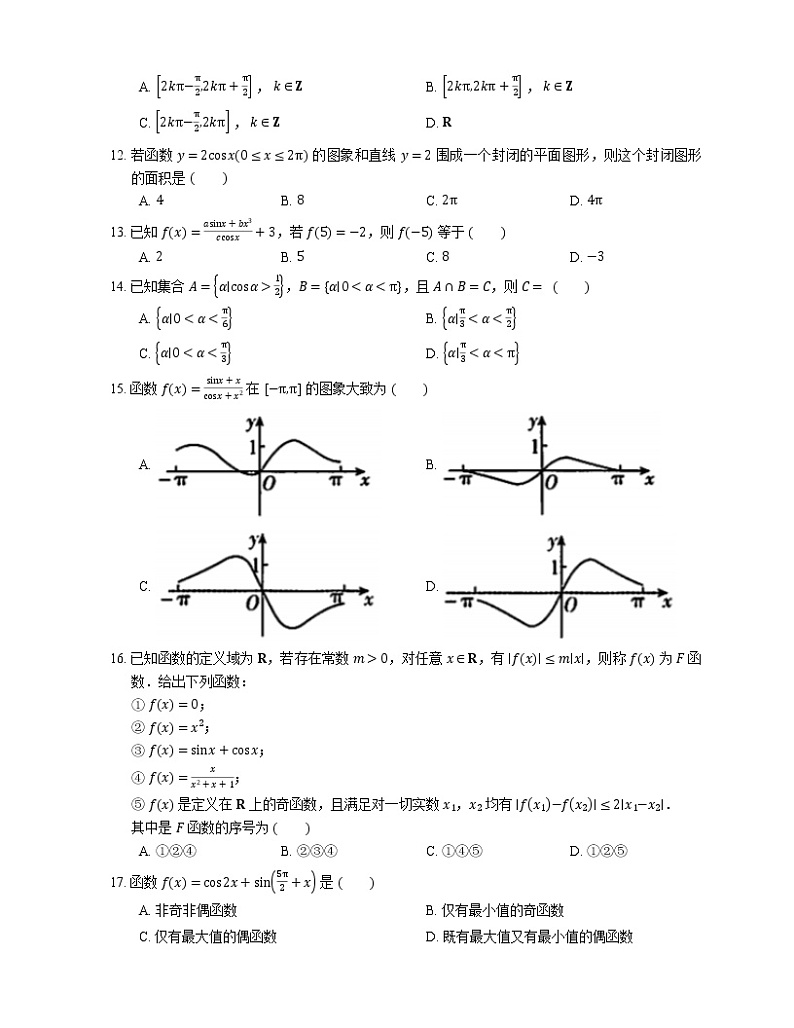
15. 函数 fx=sinx+xcsx+x2 在 −π,π 的图象大致为
A. B.
C. D.

16. 已知函数的定义域为 R，若存在常数 m>0，对任意 x∈R，有 ∣fx∣≤m∣x∣，则称 fx 为 F 函数．给出下列函数：
① fx=0；
② fx=x2；
③ fx=sinx+csx；
④ fx=xx2+x+1；
⑤ fx 是定义在 R 上的奇函数，且满足对一切实数 x1，x2 均有 ∣fx1−fx2∣≤2∣x1−x2∣．
其中是 F 函数的序号为
A. ①②④B. ②③④C. ①④⑤D. ①②⑤

17. 函数 fx=cs2x+sin5π2+x 是
A. 非奇非偶函数B. 仅有最小值的奇函数
C. 仅有最大值的偶函数D. 既有最大值又有最小值的偶函数

18. 函数 y=−sin2x−csx+94 的值域是
A. 1,134B. 134,154C. 1,154D. 54,154

19. 若函数 fx 满足 fx+1=fx，且 fx 在 −1,０上单调递增，又 α，β 为锐角三角形两内角，则
A. fsinα>fcsβB. fsinαC. fsinα>fsinβD. fcsα
20. 在下列四个函数中，在区间 0,π2 上为增函数，且以 π 为最小正周期的偶函数是
A. y=x2B. y=∣sinx∣C. y=cs2xD. y=esinx

21. 设函数 fx=csωxω>0，将 y=fx 的图象向右平移 π3 个单位后，所得的图象与原图象重合，则 ω 的最小值等于
A. 13B. 3C. 6D. 9

22. 在 △ABC 中，A>B，则以下不等式正确的个数为
① sinA>sinB ② csAsin2B ④ cs2AA. 0 个B. 1 个C. 2 个D. 3 个

23. 若 a=30.2，b=lgπ3，c=lg3cs24π，则
A. b>c>aB. b>a>cC. a>b>cD. c>a>b

24. 定义新运算 a*b 为：a*b=aa≤b,ba>b, 例如 1*2=1，3*2=2，则函数 fx=sinx*csx 的值域为
A. −1,22B. 0,22C. 0,2D. −22,22

25. 函数 y=sin2x+π3⋅csx−π6+cs2x+π3⋅sinπ6−x 的图象的一条对称轴方程是
A. x=π4B. x=π2C. x=πD. x=3π2

26. 函数 fx=cs2x+sin5π2+x 是
A. 非奇非偶函数B. 仅有最小值的奇函数
C. 仅有最大值的偶函数D. 有最大值又有最小值的偶函数

27. 函数 fx=x−1xcsx（−π≤x≤π 且 x≠0）的图象可能为
A. B.
C. D.

28. 下列命题中正确的是
A. 若 csα<0，则 α 是第一或第三象限角
B. 若 α>β，则 csαC. 若 sinα=sinβ，则 α 与 β 的终边相同
D. 若角 α 的终边在坐标轴上，则 α=12kπ，k∈Z

29. 设 a=2cs216∘−sin216∘，b=sin15∘+cs15∘，c=1+cs56∘，则 a，b，c 的大小关系为
A. c
二、选择题（共1小题；共5分）
30. 下列说法错误的是
A. y=sinx 在第一象限是增函数
B. y=cs∣x∣ 的最小正周期为 2π
C. y=tanx 是增函数
D. y=tanx 图象的所有对称中心坐标为 kπ,0，k∈Z
答案
第一部分
1. D【解析】因为 sin40∘<1sin65∘，
所以可排除A，B，C，
tan410∘=tan50∘>1>sin80∘>12>lg52，
所以D正确．
2. A
3. D【解析】因为 csx 的递增区间是 −π+2kπ,2kπ，k∈Z，
当 k=1 时，递增区间为：π,2π．
4. A
5. D
6. C【解析】①，② 正确．
7. D
8. C【解析】由题意得 fx=csx+π2=csx+π2，因此 fx 在 4,7 上是增函数是错误的．
9. D【解析】结合余弦函数的图象特征，将余弦函数图象在 x 轴下方的部分补到 x 轴上方，可得矩形 OABC，其面积为 4π．
10. A
【解析】由题意得 3cs2×4π3+φ=3cs2π3+φ+2π=3cs2π3+φ=0，
所以 2π3+φ=kπ+π2，k∈Z，
所以 φ=kπ−π6，k∈Z，取 k=0，得 ∣φ∣ 的最小值为 π6．
11. D
12. D【解析】作出函数 y=2csx,x∈0,2π 的图象，函数 y=2csx,x∈0,2π 的图象与直线 y=2 围成的平面图形，如图所示的阴影部分．
利用图象的对称性可知该封闭图形的面积等于矩形 OABC 的面积，又 ∣OA∣=2，∣OC∣=2π，所以 S封闭图形=S矩形OABC=2×2π=4π．
13. C【解析】设 gx=asinx+bx3ccsx，则 g−x=asin−x+b−x3ccs−x=−asinx+bx3ccsx=−gx，
所以 gx 是奇函数．
由 f5=−2 得 f5=g5+3=−2，
所以 g5=−5．
所以 f−5=g−5+3=−g5+3=8．
14. C【解析】因为 A=αcsα>12，B=α0<α<π，
所以 A∩B=αcsα>12,0<α<π=α0<α<π3，
即 C=α0<α<π3．
15. D
【解析】方法一：任取 x∈−π,π，
因为 f−x=sin−x+−xcs−x+−x2=−sinx+xcsx+x2=−fx，
所以 fx 在 −π,π 上为奇函数，故排除A；
当 x=π2 时，fπ2=1+π2π24=4+2ππ2>1，故排除B，C，故选D．
方法二：当 x=−π 时，f−π=sin−π+−πcs−π+−π2=−π−1+π2<0，故排除A，C；
当 x=π 时，fπ=sinπ+πcsπ+π2=π−1+π2>0.3，不是趋近于 0，故排除B．
16. C【解析】∣fx∣≤m∣x∣⇔x=0 时，f0=0，x≠0 时，fxx≤m，即过原点的弦斜率有界．
① fx=0 显然满足上面性质；
② fx=x2，f0=0 但 x≠0 时 fxx=∣x∣ 无界；
③ fx=sinx+csx，f0≠0；
④ fx=xx2+x+1，f0=0 且 x≠0 时，fxx=1x2+x+1≤43；
⑤如图所示，fx 是奇函数，则 f0=0；
又 ∣fx1−fx2∣≤2∣x1−x2∣ 恒成立，
所以所有的弦斜率绝对值有界 2，自然 2 也是过原点的弦的界，
所以 fxx≤2（也可以直接取 x2=0 得到）．
17. D【解析】因为 fx=cs2x+csx，f−x=cs−2x+cs−x=cs2x+csx=fx，
所以 fx=cs2x+csx 是偶函数．
由 fx=cs2x+csx=2cs2x+csx−1=2csx+142−98，
当 csx=1 时，fx 取得最大值 2；
当 csx=−14 时，fx 取得最小值 −98．
18. A
19. A
20. B
【解析】由 y=∣sinx∣ 的图象可以知道该函数的最小正周期是 π，并且在 0,π2 上为增函数，而 y=x2 不是周期函数；y=cs2x 在所给区间上是减函数．
21. C【解析】由题意可知 fx−π3=csωx−π3=csωx，
即 csωx−ωπ3=csωx，
所以 −ωπ3=2kπ+2πk∈Z⇒ω=−6k−6k∈Z，
所以当 k=−1 时，ωmin=6．
22. D【解析】sinA>sinB，csAsinB>0 可知 sin2A>sin2B，所以 cs2A23. C
24. A【解析】新运算 a*b 实际上是求两数（或式子）的最小值．故在同一坐标系中，画出 y=sinx 与 y=csx 在一个周期 0,2π 上的图象，如图所示，
由图可知 fxmax=22，fxmin=−1．
25. C
【解析】y=sin2x+π3−x+π6=sinπ2+x=csx，当 x=π 时，y=−1．
26. D【解析】fx=cs2x+sin5π2+x=2cs2x−1+csx=2csx+142−98 .显然有最大值又有最小值，而且在 R 上有 f−x=fx．
27. D【解析】因为 fx=x−1xcsx，
所以 f−x=−fx，
所以 fx 为奇函数，排除A，B；
当 x→π 时，fx<0，排除C．
28. D【解析】当 α=π 时，csα<0，但 α 不是第一或第三象限角，所以A不正确；
当 α=330∘，β=30∘ 时，csα=csβ，所以B不正确；
当 α=150∘，β=30∘ 时，sinα=sinβ，但是 α 与 β 的终边不相同，所以C不正确；
D 正确．
29. C【解析】a=2cs216∘−sin216∘=2cs32∘，
b=sin15∘+cs15∘=2sin60∘=2cs30∘，
c=1+cs56∘=2cs228∘=2cs28∘，
又因为 y=csx 在 0,π2 上单调递减，
所以 cs28∘>cs30∘>cs32∘，
所以 c>b>a．
第二部分
30. A， C， D
【解析】由于 390∘>30∘，且都是第一象限角，sin390∘=sin30∘=12，
故函数 y=sinx 在第一象限不是增函数，故A不正确；
y=cs∣x∣=csx，其最小正周期为 2π，故B正确；
y=tanx 的单调递增区间为 −π2+kπ,π2+kπ，k∈Z，故C不正确；
由于函数 y=tanx 图象的对称中心是 kπ2,0，k∈Z，故D不正确．
故选ACD．