精品解析：2021年内蒙古包头市昆都仑区中考二模数学试卷（解析版+原卷版）

这是一份精品解析：2021年内蒙古包头市昆都仑区中考二模数学试卷（解析版+原卷版），文件包含精品解析2021年内蒙古包头市昆都仑区中考二模数学试卷解析版doc、精品解析2021年内蒙古包头市昆都仑区中考二模数学试卷原卷版doc等2份试卷配套教学资源，其中试卷共40页， 欢迎下载使用。


2021年初中升学考试模拟试卷（二）
数学
注意事项：
1．本试卷共6页，满分为120分．考试时间为120分钟．
2．答题前，考生务必先将自己的座位号、准考证号、姓名等信息填写在试卷和答题卡的指定位置．请认真核对条形码上的相关信息后，将条形码粘贴在答题卡的指定位置上．
3．答选择题时，必须使用2B铅笔将答题卡上对应题目的答案标号涂黑，修改时用橡皮擦干净，再选涂其他答案．
4．答非选择题时，必须使用0.5毫米的黑色字迹的签字笔书写．要求字体工整，笔迹清晰，严格按题号所示的答题区域作答，超出答题区域书写的答案无效；在试卷，草稿纸上答题无效．
5．保持答题卡清洁、完整．严禁折叠、破损，严禁在答题卡上做任何标记，严禁使用涂改液、胶带纸、修正带．考试结束后，将本试卷和答题卡一并交回．
一、选择题：本大题共有12小题，每小题3分，共36分．每小题只有一个正确选项，请将答题卡上对应题目的答案标号涂黑．
1. 下列二次根式是最简二次根式的是( )
A. B. C. D.
【答案】D
【解析】
【分析】根据最简二次根式的概念逐一进行判断即可.
【详解】A. ，故A选项不符合题意；
B. ，故B选项不符合题意；
C. ，故C选项不符合题意；
D. 是最简二次根式，符合题意，
故选D.
【点睛】本题考查了最简二次根式的识别，熟练掌握二次根式的化简以及最简二次根式的概念是解题的关键.
2. 人民日报讯，2020年6月23日，中国成功发射北斗系统第55颗导航卫星，至此中国提前半年全面完成北斗三号全球卫星导航系统星座部署．北斗三号卫星上配置的新一代国产原子钟，使北斗导航系统授时精度达到了十亿分之一秒．十亿分之一用科学记数法可以表示为（ ）
A. B. C. D.
【答案】B
【解析】
【分析】十亿分之一即为，故用科学记数法表示之．
【详解】
故选：B．
【点睛】本题考查了科学记数法表示绝对值小于1的数，对于绝对值小于1的数，其科学记数法的形式为：，其中，n是正整数，它等于第一个非零数字前的零的个数．
3. 实数a、b在数轴上的对应点的位置如图所示，下列式子成立的是（　）

A. a＞b B. |a|＜|b| C. a+b＜0 D. ＞0
【答案】C
【解析】
【分析】先由数轴可知：-2＜a＜-1，0＜b＜1，且|a|＞|b|，再判断即可．
【详解】解：由数轴图可得：-2＜a＜-1，0＜b＜1，
∴a＜b，故选项A错误；
|a|＞|b|，故选项B错误；
a+b＜0，故选项C正确；
＜0，故选项D错误．
故选：C
【点睛】本题主要考查了实数与数轴，解题的关键是利用数轴确定a，b的取值范围．利用数轴可以比较任意两个实数的大小，即在数轴上表示的两个实数，右边的总比左边的大，在原点左侧，绝对值大的反而小．
4. 下列运算正确的是（ ）
A. B. C. D.
【答案】C
【解析】
【分析】利用合并同类项、积的乘方、单项式乘单项式、多项式乘多项式直接计算判断即可．
【详解】解：A. ，选项错误；
B. ，选项错误；
C. ，选项正确；
D. ，选项错误；
故选：C．
【点睛】本题考查了整式的运算，熟练掌握运算法则是解题的关键．
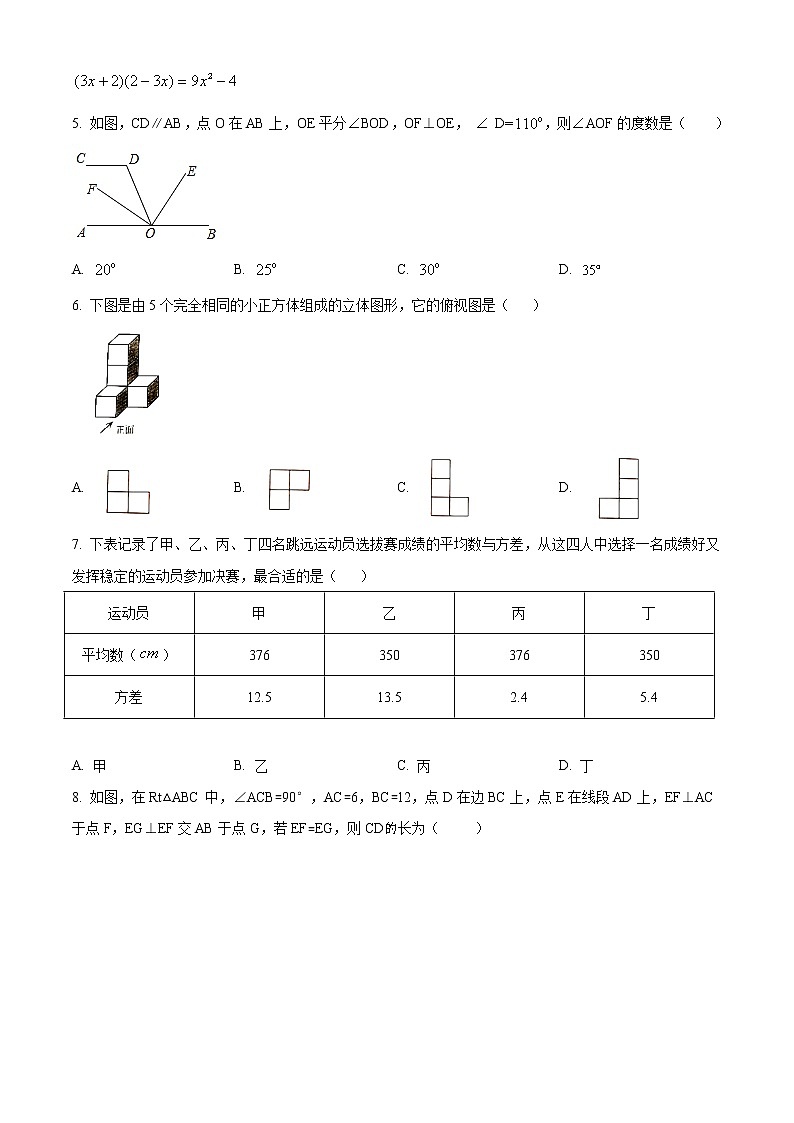
5. 如图，CD∥AB，点O在AB上，OE平分BOD，OF⊥OE， D=，则AOF的度数是（　　）

A. B. C. D.
【答案】D
【解析】
【分析】根据平行线的性质解答即可．
【详解】解：，
，

，
，
，
，
，
，
，
，
故选D．
【点睛】此题考查平行线的性质，关键是根据平行线的性质解答．
6. 下图是由5个完全相同的小正方体组成的立体图形，它的俯视图是（ ）

A. B. C. D.
【答案】B
【解析】
【分析】俯视图是从上往下看到的图形，注意能看到的棱都要体现出来，根据定义可得答案．
【详解】解：从上往下看上层看到两个正方形，下层一个正方形，
所以看到的是
故选B．
【点睛】本题考查的是简单组合体的三视图，掌握三视图的含义是解题的关键．
7. 下表记录了甲、乙、丙、丁四名跳远运动员选拔赛成绩平均数与方差，从这四人中选择一名成绩好又发挥稳定的运动员参加决赛，最合适的是（ ）
运动员
甲
乙
丙
丁
平均数（）
376
350
376
350
方差
12.5
13.5
2.4
5.4

A. 甲 B. 乙 C. 丙 D. 丁
【答案】C
【解析】
【分析】首先比较平均数，平均数相同时选择方差较小的运动员参加．
【详解】解：∵乙和丁的平均数最小，
∴从甲和丙中选择一人参加比赛，
∵丙的方差最小，
∴选择丙参赛；
故选：C．
【点睛】此题考查了平均数和方差，方差是用来衡量一组数据波动大小的量，方差越大，表明这组数据偏离平均数越大，即波动越大，数据越不稳定；反之，方差越小，表明这组数据分布比较集中，各数据偏离平均数越小，即波动越小，数据越稳定．
8. 如图，在Rt△ABC中，∠ACB=90°，AC=6，BC=12，点D在边BC上，点E在线段AD上，EF⊥AC于点F，EG⊥EF交AB于点G，若EF=EG，则CD的长为（ ）

A. 3.6 B. 4 C. 4.8 D. 5
【答案】B
【解析】
【分析】过点D作DH⊥BC交AB于点H，根据△AFE∽△ACD和△AEG∽△ADH可得DC=DH，再由△BDH∽△BCA，根据相似三角形的性质列出方程即可求出CD.
【详解】解：过点D作DH⊥BC交AB于点H，
∵EF⊥AC，∴EF∥BC，
∴△AFE∽△ACD，∴，
∵DH⊥BC，EG⊥EF，∴DH∥EG，
∴△AEG∽△ADH，∴，
∴
∵EF=EG，
∴DC=DH，
设DH=DC=x，则BD=12-x，
又∵△BDH∽△BCA，
∴，即，
解得：x=4，即CD=4，
故选B.

【点睛】本题考查了相似三角形的判定和性质，根据相似的性质得到DC=DH是解题关键.
9. 如图，⊙O是等边△ABC的内切圆，分别切AB，BC，AC于点E，F，D，P是上一点，则∠EPF的度数是（ ）

A. 65° B. 60° C. 58° D. 50°
【答案】B
【解析】
【分析】连接OE，OF．求出∠EOF的度数即可解决问题．
【详解】解：如图，连接OE，OF．
∵⊙O是△ABC的内切圆，E，F是切点，
∴OE⊥AB，OF⊥BC，
∴∠OEB=∠OFB=90°，
∵△ABC是等边三角形，
∴∠B=60°，
∴∠EOF=120°，
∴∠EPF=∠EOF=60°，
故选：B．

【点睛】本题考查三角形的内切圆与内心，切线的性质，圆周角定理等知识，解题的关键是熟练掌握基本知识，属于中考常考题型．
10. 若菱形ABCD的一条对角线长为8，边CD的长是方程x2﹣10x+24＝0的一个根，则该菱形ABCD的周长为（　　）
A 16 B. 24 C. 16或24 D. 48
【答案】B
【解析】
【分析】解方程得出x＝4或x＝6，分两种情况：①当AB＝AD＝4时，4+4＝8，不能构成三角形；②当AB＝AD＝6时，6+6＞8，即可得出菱形ABCD的周长．
【详解】解：如图所示：
∵四边形ABCD是菱形，
∴AB＝BC＝CD＝AD，
∵x2﹣10x+24＝0，
因式分解得：（x﹣4）（x﹣6）＝0，
解得：x＝4或x＝6，
分两种情况：
①当AB＝AD＝4时，4+4＝8，不能构成三角形；
②当AB＝AD＝6时，6+6＞8，
∴菱形ABCD的周长＝4AB＝24．
故选：B．

【点睛】本题考查菱形的性质、解一元二次方程-因式分解法、三角形的三边关系，熟练掌握并灵活运用是解题的关键．
11. 如图，在平面直角坐标系中，矩形ABCD的顶点A，C分别在x轴，y轴的正半轴上，点D（-2，3），AD=5，若反比例函数 （k＞0，x＞0）的图象经过点B，则k的值为（　　）

A. B. 8 C. 10 D.
【答案】D
【解析】
【分析】先由D（-2，3），AD=5，求得A（2，0），即得AO=2；设AD与y轴交于E，求得E（0，1.5），即得EO=1.5；作BF垂直于x轴于F，求证△AOE ∽△CDE，可得，求证△AOE∽△BFA，可得AF=2，BF=，进而可求得B（4，）；将B（4，）代入反比例函数，即可求得k的值．
【详解】解：如图，过D作DH垂直x轴于H，设AD与y轴交于E，过B作BF垂直于x轴于F，

∵点D（-2，3），AD=5，
∴DH=3，
∴，
∴A（2，0），即AO=2，
∵D（-2，3），A（2，0），
∴AD所在直线方程为：，
∴E（0，1.5），即EO=1.5，
∴,
∴ED=AD- AE=5-=，
∵∠AOE=∠CDE，∠AEO=∠CED，
∴△AOE ∽△CDE，
∴,
∴,
∴在矩形ABCD中，，
∵∠EAO+∠BAF=90°，
又∠EAO+∠AEO=90°，
∴∠AEO=∠BAF，
又∵∠AOE=∠BFA，
∴△BFA∽△AOE，
∴,
∴代入数值，可得AF=2，BF=，
∴OF=AF+AO=4，
∴B（4，），
∴将B（4，）代入反比例函数，得，
故选：D．
【点睛】本题主要考查了待定系数法求反比例函数的系数、相似三角形的判定与性质、勾股定理、矩形的性质等知识．解题关键是通过求证△AOE ∽△CDE，△AOE∽△BFA，得到B点坐标，将B点坐标代入反比例函数，即可得解．
12. 如图，矩形中，相交于点O，过点B作交于点F，交于点M，过点D作交于点E，交于点N，连接．则下列结论：
①；②；
③；④当时，四边形是菱形．
其中，正确结论的个数是（ ）

A. 1个 B. 2个 C. 3个 D. 4个
【答案】D
【解析】
【分析】通过判断△AND≌△CMB即可证明①，再判断出△ANE≌△CMF证明出③，再证明出△NFM≌△MEN，得到∠FNM=∠EMN，进而判断出②，通过 DF与EB先证明出四边形为平行四边形，再通过三线合一以及内角和定理得到∠NDO=∠ABD=30°，进而得到DE=BE，即可知四边形为菱形．
【详解】∵BF⊥AC
∴∠BMC=90°
又∵
∴∠EDO=∠MBO，DE⊥AC
∴∠DNA=∠BMC=90°
∵四边形ABCD为矩形
∴AD=BC，AD∥BC，DC∥AB
∴∠ADB=∠CBD
∴∠ADB-∠EDO=∠CBD-∠MBO即∠AND=∠CBM
在△AND与△CMB
∵
∴△AND≌△CMB(AAS)
∴AN=CM，DN=BM，故①正确．
∵AB∥CD
∴∠NAE=∠MCF
又∵∠DNA=∠BMC=90°
∴∠ANE=∠CMF=90°
在△ANE与△CMF中
∵
∴△ANE≌△CMF（ASA）
∴NE=FM，AE=CF，故③正确．
在△NFM与△MEN中
∵
∴△NFM≌△MEN（SAS）
∴∠FNM=∠EMN
∴NF∥EM，故②正确．
∵AE=CF
∴DC-FC=AB-AE，即DF=EB
又根据矩形性质可知DF∥EB
∴四边形DEBF为平行四边
根据矩形性质可知OD=AO，
当AO=AD时，即三角形DAO为等边三角形
∴∠ADO=60°
又∵DN⊥AC
根据三线合一可知∠NDO=30°
又根据三角形内角和可知∠ABD=180°-∠DAB-∠ADB=30°
故DE=EB
∴四边形DEBF为菱形，故④正确．
故①②③④正确
故选D．
【点睛】本题矩形性质、全等三角形性质与证明、菱形的判定，能够找对相对应的全等三角形是解题关键．
二、填空题：本大题共有8小题，每小题3分，共24分．请将答案填在答题卡上的对应横线上．
13. 函数自变量x的取值范围是 _____.
【答案】x≥1且x≠3
【解析】
【分析】根据分式成立的条件，二次根式成立的条件列不等式组，从而求解.
【详解】解：根据题意得：，
解得x≥1，且x≠3，
即：自变量x取值范围是x≥1且x≠3．
故答案为x≥1且x≠3．
【点睛】本题考查函数自变量的取值范围；分式有意义的条件；二次根式有意义的条件．
14. 已知关于x的分式方程的解为非负数，则正整数m的所有个数为_______个．
【答案】4
【解析】
【分析】求出分式方程的解，根据题意建立不等式，求得解集，后确定正整数解得个数，注意方程的增根时对应的m值，要删除．
【详解】∵，
∴m+2（x-1）=3，
解得x=，
∵分式方程的解为非负数，
∴≥0，
解得m≤5，
∴正整数m的值为1,2,3,4,5，
∵x=1是分式方程的增根，
∴m=3，要扣除，
∴正整数m的所有个数为4个，
故答案为：4．
【点睛】本题考查了分式方程的解法，解不等式，求不等式的正整数解，分式方程的增根，熟练解分式方程，根据解的非负数性质构造不等式并求其特殊解是解题的关键，注意增根．
15. 计算：的结果是______．
【答案】
【解析】
【分析】利用积的乘方的逆运算和同底数幂乘法的逆运算解答．
【详解】
=
=
=，
故答案为：．
【点睛】此题考查积的乘方的逆运算和同底数幂乘法的逆运算，平方差计算公式，二次根式的混合运算，熟记运算公式是解题的关键．
16. 如图，正方形ABCD中，点E、F分别在边CD，AD上，BE与CF交于点G．若BC＝4，DE＝AF＝1，则GF的长为_____．

【答案】2.6
【解析】
【分析】先证明△CDF≌△BCE，得到∠BGC＝90°，利用面积法求出，求出CF＝5，即可求出GF．
【详解】解：∵四边形ABCD为正方形，BC＝4，
∴∠CDF＝∠BCE＝90°，AD＝DC＝BC＝4，
又∵DE＝AF＝1，
∴CE＝DF＝3，
∴在△CDF和△BCE中，
，
∴△CDF≌△BCE（SAS），
∴∠DCF＝∠CBE，
∵∠DCF+∠BCF＝90°，
∴∠CBE+∠BCF＝90°，
∴∠BGC＝90°，
∵在Rt△BCE中，BC＝4，CE＝3，
∴
∴BE•CG＝BC•CE，
∴，
∵△CDF≌△BCE（SAS），
∴CF＝BE＝5，
∴GF＝CF﹣CG＝5﹣＝2.6．
故答案为：2.6．
【点睛】本题考查了正方形的性质，勾股定理等知识，证明△CDF≌△BCE是解题关键．
17. 婷婷和她妈妈玩猜拳游戏．规定每人每次至少要出一个手指，两人出拳的手指数之和为偶数时婷婷获胜．那么，婷婷获胜的概率为______．

【答案】
【解析】
【分析】根据题意，可用列举法、列表法或树状统计图来计算出总次数和婷婷获胜的次数，从而求出婷婷获胜的概率
【详解】解：根据题意，一共有25个等可能的结果，即(1,1)，(1,2)，(1,3)，(1,4)，(1,5)，(2,1)，(2,2)，(2,3)，(2,4)，(2,5)，(3,1)，(3,2)，(3,3)，(3,4)，(3,5)，(4,1)，(4,2)，(4,3)，(4,4)，(4,5)，(5,1)，(5,2)，(5,3)，(5,4)，(5,5);
两人出拳的手指数之和为偶数的结果有13个，
所以婷婷获胜的概率为
故答案为：
【点睛】本题考查的是用列举法等来求概率，找出所有可能的结果数和满足要求的结果数是解决问题的关键．
18. 如图，在矩形中，．分别以点为圆心，以大于的长为半径画弧，两弧相交于点和．作直线分别与交于点，则__________．

【答案】2．
【解析】
【分析】连接DN，在矩形ABCD中，AD=4，AB=8，根据勾股定理可得BD的长，根据作图过程可得，MN是BD的垂直平分线，所以DN=BN，在Rt△ADN中，根据勾股定理得DN的长，在Rt△DON中，根据勾股定理得ON的长，进而可得MN的长．
【详解】如图，连接DN，

在矩形ABCD中，AD=4，AB=8，
∴BD=，
根据作图过程可知：
MN是BD的垂直平分线，
∴DN=BN，OB=OD=2，
∴AN=AB-BN=AB-DN=8-DN，
在Rt△ADN中，根据勾股定理，得
DN2=AN2+AD2，
∴DN2=（8-DN）2+42，
解得DN=5，
在Rt△DON中，根据勾股定理，得
ON=，
∵CD∥AB，
∴∠MDO=∠NBO，
∠DMO=∠BNO，
∵OD=OB，
∴△DMO≌△BNO（AAS），
∴OM=ON=，
∴MN=2．
故答案为：2．
【点睛】本题考查了作图-基本作图、线段垂直平分线的性质、勾股定理、矩形的性质，解决本题的关键是掌握线段垂直平分线的性质．
19. 将二次函数的图象先向下平移1个单位，再向右平移3个单位，得到的图象与一次函数的图象有公共点，则实数b的取值范围是_____________．
【答案】
【解析】
【分析】先根据平移原则：上→加，下→减，左→加，右→减写出解析式，再列方程组，有公共点则△≥0，则可求出b的取值．
【详解】解：由题意得：平移后得到的二次函数的解析式为：y=（x-3）2-1，
则，
∴（x-3）2-1=2x+b，
整理得，x2-8x+8-b=0，
∴△=（-8）2-4×1×（8-b）≥0，
解得，b≥-8，
故答案是：b≥-8．
【点睛】主要考查的是函数图象的平移和两函数的交点问题，两函数有公共点：说明两函数有一个交点或两个交点，可利用方程组→一元二次方程→△≥0的问题解决．
20. 如图，在平面直角坐标系中，点A的坐标是，点B在第一象限内，，点E是线段上的一个动点，连接，将射线绕点E顺时针旋转交于点F，当最短时点F的坐标是____________．

【答案】
【解析】
【分析】由已知易得△BEF∽△BAE，则对应边成比例，可得，从而当BE最小时，BF最小，而当BE⊥x轴时，BE最小即垂线段最短，此时可得EF⊥AB，过点F作FD⊥x轴于点D，利用30゜角的直角三角形的性质和勾股定理，即可求得F点的坐标．
【详解】∵∠BEF=∠BAO=60゜，∠B=∠B
∴△BEF∽△BAE
∴
∴
∴当BE最小时，BF也最小
而当BE⊥x轴时，垂线段最短，故BE最小，因而BF也最小
∴∠FEA=90゜−∠BEF=30゜
∴∠EFA=180゜−∠FEA−∠BAO=90゜
即EF⊥AB
过点F作FD⊥x轴于点D，如图
在Rt△BEA中，∠ABE=90゜-∠BAO=30゜
∴AE=
∵在Rt△FEA中，∠FEA=30゜
∴
在Rt△FDA中，∠AFD=90゜-∠BAO=30゜
∴
由勾股定理得：
∵OD=
∴D点坐标为

【点睛】本题考查了垂线段最短，相似三角形的判定与性质，30゜角的直角三角形的性质，勾股定理等知识，关键是根据相似三角形的性质，把BF最短转化为线段BE最短．
三、解答题：本大题共有6小题，共60分．请将必要的文字说明、计算过程或推理过程写在答题卡的对应位置．
21. 一只不透明袋子中装有1个白球和若干个红球，这些球除颜色外都相同，某课外学习小组做摸球试验：将球搅匀后从中任意摸出1个球，记下颜色后放回、搅匀，不断重复这个过程，获得数据如下：
摸球的次数
200
300
400
1000
1600
2000
摸到白球的频数
72
93
130
334
532
667
摸到白球的频率
0.3600
0.3100
0.3250
0.3340
0.3325
0.3335
（1）该学习小组发现，随着摸球次数的增多，摸到白球的频率在一个常数附近摆动，请直接写出这个常数（精确到0.01），由此估出红球有几个？
（2）在这次摸球试验中，从袋中随机摸出1个球，记下颜色后放回，再从中随机摸出1个球，利用画树状图或列表的方法表示所有可能出现的结果，并求两次摸到的球恰好1是个白球，1个是红球的概率．
【答案】（1）这个常数是0.33，由此估出红球有2个；（2）
【解析】
【分析】（1）计算频率的平均数，后按照精确度求得近似数即可；根据概率公式建立方程求解即可；
（2）画树状图求解即可．
【详解】（1）根据题意，得

＝0.3325
≈0.33，
设有x个红球，根据题意，得，
解得x≈2
经检验，符合题意．
故这个常数是0.33，由此估出红球有2个．
（2）画树状图如下：

据图知，所有等可能的情况有9种，其中恰好摸到1个白球，1个红球的情况有4种，
则P（恰好摸到1个白球，1个红球）．
所以从该袋中摸出2个球，恰好摸到1个白球、1个红球的结果的概率为．
【点睛】本题考查了用频率估计概率，画树状图计算概率，准确理解频率估计概率的意义，熟练画树状图是解题的关键．
22. 如图，一艘渔船位于小岛的北偏东方向，距离小岛的点处，它沿着点的南偏东的方向航行．

（1）渔船航行多远距离小岛最近(结果保留根号)？
（2）渔船到达距离小岛最近点后，按原航向继续航行到点处时突然发生事故，渔船马上向小岛上的救援队求救，问救援队从处出发沿着哪个方向航行到达事故地点航程最短，最短航程是多少(结果保留根号)？
【答案】（1）；（2）南偏东；
【解析】
【分析】（1）过点作的垂线交于点，则AD为所求，根据已知条件得到∠BAD=45°即可解答；
（2）根据特殊角的锐角三角函数值得到∠C=30°，∠DBC=60°，从而求出BC的长度，再求出∠DBE的度数，即可得到∠EBC的度数．
【详解】解：（1）过点作的垂线交于点，

∵垂线段最短，上的点距离点最近，即为所求，
由题意可知：∠BAF=30°，∠CAF=15°，
∴，
∴渔船航行时，距离小岛最近．
（2）在中，，
∠DBC=60°，

∵∠ABD=45°，∠ABE=90°-30°=60°，
∴，
.
答：从处沿南偏东出发，最短行程.
【点睛】本题考查了解直角三角形的应用中的方向角问题，结合航海中的实际问题，将解直角三角形的相关知识有机结合，体现了数学应用于实际生活的思想．
23. 某企业接到生产一批设备的订单，要求不超过12天完成．这种设备的出厂价为1200元/台，该企业第一天生产22台设备，第二天开始，每天比前一天多生产2台．若干天后，每台设备的生产成本将会增加，设第x天（x为整数）的生产成本为m（元台），m与x的关系如图所示．

（1）若第x天可以生产这种设备y台，则y与x的函数关系式为______，x的取值范围为______；
（2）第几天时，该企业当天的销售利润最大？最大利润为多少？
（3）求当天销售利润低于10800元的天数．
【答案】（1）；
（2）第6天时，该企业利润最大，12800元.
（3）7天
【解析】
【分析】（1）根据题意确定一次函数的解析式，实际问题中x的取值范围要使实际问题有意义；
（2）求出当天利润与天数的函数解析式，确定其最大值即可；
（3）根据（2）中的函数解析式列出不等式方程即可解答．
【详解】（1）根据题意，得y与x的解析式为：（）
（2）设当天的当天的销售利润为w元，则根据题意，得
当1≤x≤6时，
w=（1200-800）（2x+20）=800x+8000，
∵800＞0，∴w随x的增大而增大，
∴当x=6时，w最大值=800×6+8000=12800．
当6＜x≤12时，
易得m与x的关系式：m=50x+500
w=[1200-（50x+500）]×（2x+20）
=-100x2+400x+14000=-100（x-2）2+14400．
∵此时图象开口向下，在对称轴右侧，w随x的增大而减小，天数x为整数，
∴当x=7时，w有最大值，为11900元，
∵12800＞11900，
∴当x=6时，w最大，且w最大值=12800元，
答：该厂第6天获得的利润最大，最大利润是12800元．
（3）由（2）可得，
1≤x≤6时，

解得：x＜3.5
则第1-3天当天利润低于10800元，
当6＜x≤12时，

解得x＜-4（舍去）或x＞8
则第9-12天当天利润低于10800元，
故当天销售利润低于10800元的天数有7天．
【点睛】本题主要考查一次函数和二次函数的应用，解题关键在于理解题意，利用待定系数法确定函数的解析式，并分类讨论．
24. 已知，如图，AB是⊙O的直径，点C为⊙O上一点，OF⊥BC于点F，交⊙O于点E，AE与BC交于点H，点D为OE的延长线上一点，且∠ODB=∠AEC．
（1）求证：BD是⊙O的切线；
（2）求证：CE2=EH•EA；
（3）若⊙O的半径为5，sinA=，求BH的长．

【答案】（1）见解析；（2）见解析；（3）.
【解析】
【分析】（1）由圆周角定理和已知条件证出∠ODB=∠ABC，再证出∠ABC+∠DBF=90°，即∠OBD=90°，即可得出BD是⊙O的切线；
（2）连接AC，由垂径定理得出，得出∠CAE=∠ECB，再由公共角∠CEA=∠HEC，证明△CEH∽△AEC，得出对应边成比例，即可得出结论；
（3）连接BE，由圆周角定理得出∠AEB=90°，由三角函数求出BE，再根据勾股定理求出EA，得出BE=CE=6，由（2）的结论求出EH，然后根据勾股定理求出BH即可．
【详解】（1）证明：∵∠ODB=∠AEC，∠AEC=∠ABC，
∴∠ODB=∠ABC，
∵OF⊥BC，
∴∠BFD=90°，
∴∠ODB+∠DBF=90°，
∴∠ABC+∠DBF=90°，
即∠OBD=90°，
∴BD⊥OB，
∴BD是⊙O的切线；
（2）证明：连接AC，如图1所示：

∵OF⊥BC，
∴，
∴∠CAE=∠ECB，
∵∠CEA=∠HEC，
∴△CEH∽△AEC，
∴，
∴CE2=EH•EA；
（3）解：连接BE，如图2所示：

∵AB是⊙O的直径，
∴∠AEB=90°，
∵⊙O的半径为5，sin∠BAE=，
∴AB=10，BE=AB•sin∠BAE=10×=6，
∴EA===8，
∵，
∴BE=CE=6，
∵CE2=EH•EA，
∴EH==，
在Rt△BEH中，BH===．
25. 如图，在平面直角坐标系xOy中，矩形ABCD的边AB＝4，BC＝6．若不改变矩形ABCD的形状和大小，当矩形顶点A在x轴的正半轴上左右移动时，矩形的另一个顶点D始终在y轴的正半轴上随之上下移动．
(1)当∠OAD＝30°时，求点C的坐标；
(2)设AD的中点为M，连接OM、MC，当四边形OMCD的面积为时，求OA的长；
(3)当点A移动到某一位置时，点C到点O的距离有最大值，请直接写出最大值，并求此时cos∠OAD的值．

【答案】(1)点C的坐标为(2，3+2)；(2)OA＝3；(3)OC的最大值为8，cos∠OAD＝．
【解析】
【分析】(1)作CE⊥y轴，先证∠CDE＝∠OAD＝30°得CE＝CD＝2，DE＝，再由∠OAD＝30°知OD＝AD＝3，从而得出点C坐标；
(2)先求出S△DCM＝6，结合S四边形OMCD＝知S△ODM＝，S△OAD＝9，设OA＝x、OD＝y，据此知x2+y2＝36，xy＝9，得出x2+y2＝2xy，即x＝y，代入x2+y2＝36求得x的值，从而得出答案；
(3)由M为AD的中点，知OM＝3，CM＝5，由OC≤OM+CM＝8知当O、M、C三点在同一直线时，OC有最大值8，连接OC，则此时OC与AD的交点为M，ON⊥AD，证△CMD∽△OMN得，据此求得MN＝，ON＝，AN＝AM﹣MN＝，再由OA＝及cos∠OAD＝可得答案．
【详解】(1)如图1，过点C作CE⊥y轴于点E，

∵矩形ABCD中，CD⊥AD，
∴∠CDE+∠ADO＝90°，
又∵∠OAD+∠ADO＝90°，
∴∠CDE＝∠OAD＝30°，
∴在Rt△CED中，CE＝CD＝2，DE＝＝2，
在Rt△OAD中，∠OAD＝30°，
∴OD＝AD＝3，
∴点C的坐标为(2，3+2)；
(2)∵M为AD的中点，
∴DM＝3，S△DCM＝6，
又S四边形OMCD＝，
∴S△ODM＝，
∴S△OAD＝9，
设OA＝x、OD＝y，则x2+y2＝36，xy＝9，
∴x2+y2＝2xy，即x＝y，
将x＝y代入x2+y2＝36得x2＝18，
解得x＝3(负值舍去)，
∴OA＝3；
(3)OC的最大值为8，
如图2，M为AD的中点，

∴OM＝3，CM＝＝5，
∴OC≤OM+CM＝8，
当O、M、C三点在同一直线时，OC有最大值8，
连接OC，则此时OC与AD的交点为M，过点O作ON⊥AD，垂足为N，
∵∠CDM＝∠ONM＝90°，∠CMD＝∠OMN，
∴△CMD∽△OMN，
∴，即，
解得MN＝，ON＝，
∴AN＝AM﹣MN＝，
在Rt△OAN中，OA＝，
∴cos∠OAD＝．
【点睛】本题是四边形的综合问题，解题的关键是掌握矩形的性质、勾股定理、相似三角形的判定与性质等知识点．
26. 如图，抛物线与x轴交于A，B两点（点A在点B的左侧），与y轴交于点C．直线l与抛物线交于A，D两点，与y轴交于点E，点D的坐标为．

（1）求A，B两点的坐标及直线l的函数表达式；
（2）若点P是抛物线上的点，点P的横坐标为，过点P作轴，垂足为M．与直线l交于点N，当点N是线段的三等分点时，求点P的坐标；
（3）若点Q是y轴上的点，且，求点Q的坐标．
【答案】（1）；；（2）点P的坐标为或；（3）点Q的坐标为或
【解析】
【分析】（1）令y=0，便可由抛物线的解析式求得A、B点坐标，用待定系数法求得直线AD的解析式；
（2）设P（m，m2-m-3），用m表示N点坐标，分两种情况：PM=3MN；PM=3PN．分别列出m的方程进行解答便可；
（3）分两种情况，Q点在y轴正半轴上时；Q点在y轴负半轴上时．再分别解决问题．
【详解】解：（1）令，得，解得，，或，
∴，
设直线l的解析式为，
把，D代入，则有，
解得，，
∴直线l的解析式为；
（2）如图1，根据题意可知，点P与点N的坐标分别为，
∴，，，

分两种情况：
①当时，得，
解得，，或（舍），
∴；
②当时，
得，
解得，，或（舍），
∴；
∴当点N是线段的三等分点时，点P的坐标为或；
（3）∵直线与y轴交于点E，
∴点E的坐标为，
分两种情况：①如图2.当点Q在y轴的正半轴上时，记为点，

过作于点H，则，
∵，
∴，
∴，即，
∴，
∵，
∴，
∴，
∴，
连接，
∵，
∴轴，
∴，
∴，
∴，
∴，
∴；
②如图3，当点Q在y轴的负半轴上时，记为点，

过作于G，则，
∵，
∴，
∴，即，
∴，
∵，，
∴，
∴，
∴，
由①可知，，
∴，
∴，
∴，
∴，
∴，
∴，
综上，点Q的坐标为或
【点睛】本题是二次函数的综合题，主要考查了二次函数的图象与性质，待定系数法，等腰三角形的性质与判定，勾股定理，相似三角形的判定与性质，熟练掌握相似三角形的判定与性质是解题的关键．