初中数学北师大版八年级下册1 等腰三角形优秀达标测试

这是一份初中数学北师大版八年级下册1 等腰三角形优秀达标测试，共7页。
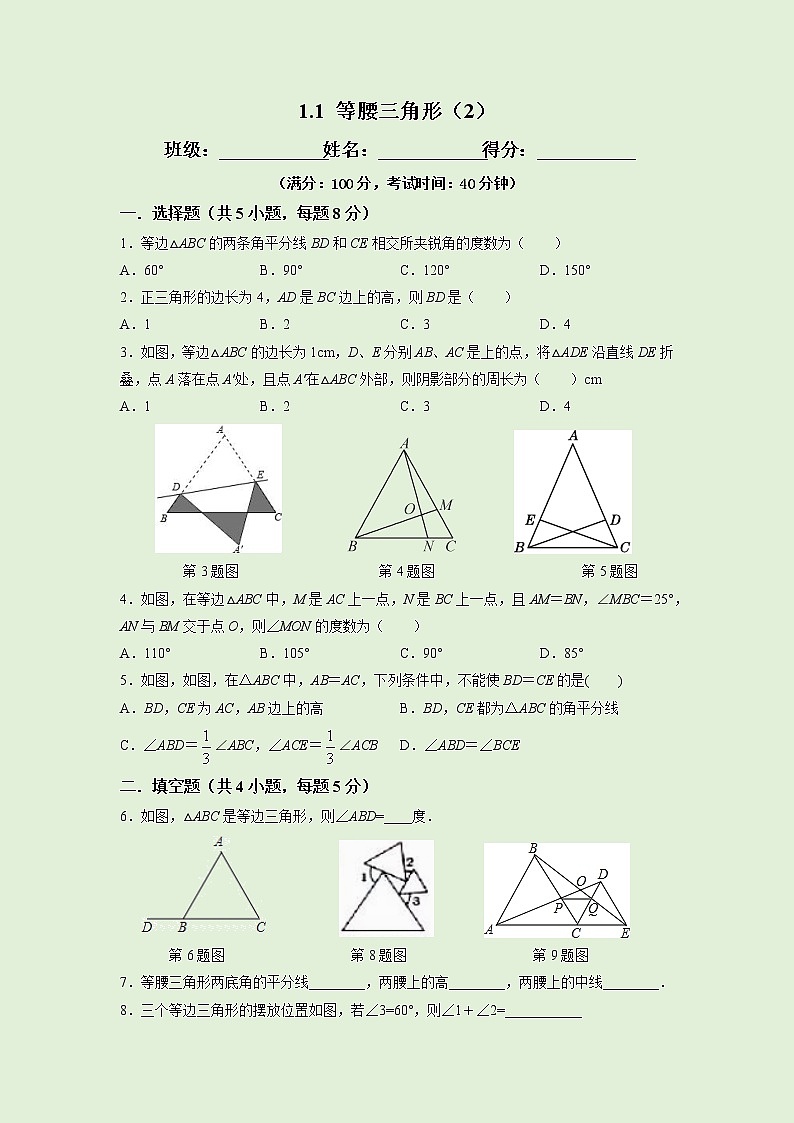
1.1 等腰三角形（2）班级：___________姓名：___________得分：__________（满分：100分，考试时间：40分钟）一．选择题（共5小题，每题8分）1．等边△ABC的两条角平分线BD和CE相交所夹锐角的度数为（    ）A．60°       B．90°       C．120°       D．150°2．正三角形的边长为4，AD是BC边上的高，则BD是（    ）A．1          B．2          C．3         D．43．如图，等边△ABC的边长为1cm，D、E分别AB、AC是上的点，将△ADE沿直线DE折叠，点A落在点A′处，且点A′在△ABC外部，则阴影部分的周长为（    ）cmA．1       B．2       C．3       D．4                 第3题图                    第4题图                     第5题图4．如图，在等边△ABC中，M是AC上一点，N是BC上一点，且AM＝BN，∠MBC＝25°，AN与BM交于点O，则∠MON的度数为（    ）A．110°       B．105°       C．90°       D．85°5．如图，如图，在△ABC中，AB＝AC，下列条件中，不能使BD＝CE的是(　　)A．BD，CE为AC，AB边上的高    B．BD，CE都为△ABC的角平分线 C．∠ABD＝∠ABC，∠ACE＝∠ACB D．∠ABD＝∠BCE二．填空题（共4小题，每题5分）6．如图，△ABC是等边三角形，则∠ABD=____度．                 第6题图                  第8题图                  第9题图7．等腰三角形两底角的平分线________，两腰上的高________，两腰上的中线________．8．三个等边三角形的摆放位置如图，若∠3=60°，则∠1＋∠2=___________9．如图，C为线段AE上一动点（不与点A，E重合），在AE同侧分别作等边△ABC和等边△CDE，AD与BE交于点O，AD与BC交于点P，BE与CD交于点Q，连接PQ．则下列结论：①AD=BE；②PQ∥AE；③AP=BQ；④DE=DP．其中正确的是______．三．解答题（共3小题，第10题10分，第11、12题各15分）10．如图,在△ABC中,AB=AC,D,E分别是AB,AC的中点,且CD=BE,△ADC与△AEB全等吗?请说明理由.    11．如图，在等边三角形ABC中，D是AB边上的动点，以CD为一边，向上作等边三角形EDC，连接AE.(1)△DBC和△EAC全等吗？请说出你的理由；(2)试说明AE∥BC.  12．如图，△ABC为等边三角形，点P为边BC上一点，在AC上取一点D，使AD＝AP.(1)若∠APD＝80°，求∠DPC的度数；(2)若∠APD＝α，求∠BAP(用含α的式子表示)．     试题解析1．A【解析】据已知条件和等边三角形的性质可知：∠1=∠2=∠ABC=30°，所以∠3=∠1+∠2=60°．2．B【解析】根据等边三角形三线合一的性质即可解答.解：因为在△ABC中，AD是BC边上的高，所以BD.故B项正确.【点睛】3．C【解析】由题意得到DA′＝DA，EA′＝EA，经分析判断得到阴影部分的周长等于△ABC的周长即可解决问题．解：如图，由题意得：DA′＝DA,EA′＝EA，∴阴影部分的周长＝DA′＋EA′＋DB＋CE＋BG＋GF＋CF＝(DA＋BD)＋(BG＋GF＋CF)＋(AE＋CE)＝AB＋BC＋AC＝1＋1＋1＝3(cm)故选C.4．A【解析】根据等边三角形的性质可得∠A=∠B=60°，又因为AM=BN，AB=AB，所以△AMB≌△BNA，从而得到∠NAB=∠MBA=60°-∠MBC=35°，则∠MON=∠AOB=180°-2×35°=110°．解：∵△ABC是等边三角形，∴∠A=∠B=60°，∵AM=BN，AB=AB，在△AMB与△BNA中，，∴△AMB≌△BNA（SAS），∴∠NAB=∠MBA=60°-∠MBC=35°，∴∠AOB=180°-2×35°=110°，∵∠MON=∠AOB，∴∠MON=110°．故选A．5．D【解析】利用等腰三角形的性质及特殊的性质进行判断即可得出答案.解：根据等腰三角形腰上的高相等、底角的平分线相等，即可得出BD＝CE，故选项A、B不符题意；根据等腰三角形特殊性质，由∠ABD＝∠ABC，∠ACE＝∠ACB，即可得出BD＝CE，故选项C不符题意；故选D.6．120【解析】根据等边三角形的三个内角都等于60度求得∠ABC=60°，然后根据邻补角互补即可求出∠ABD的度数．解：∵△ABC是等边三角形，∴∠ABC=60°，∴∠ABD=180°-∠ABC=120°．故答案为：120．7．相等，相等，相等【解析】根据等腰三角形特殊的性质：等腰三角形两底角的平分线相等，两腰上的高相等，两腰上的中线相等，即可得出答案．故答案为：相等，相等，相等．8．120°【解析】先根据图中是三个等边三角形可知三角形各内角等于60°，用∠1，∠2，∠3表示出△ABC各角的度数，再根据三角形内角和定理即可得出结论．解：∵图中是三个等边三角形，∠3＝60°，∴∠ABC＝180°﹣60°﹣60°＝60°，∠ACB＝180°﹣60°﹣∠2＝120°﹣∠2，∠BAC＝180°﹣60°﹣∠1＝120°﹣∠1．∵∠ABC+∠ACB+∠BAC＝180°，∴60°+（120°﹣∠2）+（120°﹣∠1）＝180°，∴∠1+∠2＝120°．故答案为：120°．9．①②③【解析】利用三角形全等，得到结论，利用排除法即可求解．解：∵等边△ABC和等边△CDE，∴AC=BC，CD=CE，∠ACB=∠DCE=60°，∴∠ACB+∠BCD=∠DCE+∠BCD，即∠ACD=∠BCE，∴△ACD≌△BCE（SAS），∴AD=BE①成立， 由（1）中的全等得∠CBE=∠DAC，又∠ACB=∠DCE=60°，∴∠BCD=60°，即∠ACP=∠BCQ，又AC=BC，∴△CQB≌△CPA（ASA），∴CP=CQ，又∵∠PCQ=60°可知△PCQ为等边三角形，∴∠PQC=∠DCE=60°，∴PQ∥AE②成立， 由△CQB≌△CPA得AP=BQ③成立，故答案为：①②③10．答案见解析【解析】由中点定义及AB=AC，可得到AD=AE，再通过SAS证明△ADC≌△AEB即可．证明：△ADC≌△AEB．理由如下：∵AB=AC，D，E分别是AB，AC的中点，∴AD=AE．在△ADC和△AEB中，∵AC=AB，∠A=∠A(公共角)，AD=AE，∴△ADC≌△AEB(SAS)．11．(1)△DBC和△EAC全等，理由见解析；（2）见解析【解析】(1)要证两个三角形全等，已知的条件有AC=BC，CE=CD，我们发现∠BCD和∠ACE都是60°减去一个∠ACD，因此两三角形全等的条件就都凑齐了(SAS)；(2)要证AE∥BC，关键是证∠EAC=∠ACB，由于∠ACB=∠ACB，那么关键是证∠EAC=∠ACB，根据(1)的全等三角形，我们不难得出这两个角相等，也就得出了证平行的条件．解：(1)△DBC和△EAC全等．理由：∵△ABC和△EDC都是等边三角形，∴∠ACB＝60°，∠DCE＝60°，AC＝BC，DC＝EC，∴∠BCD＝60°－∠ACD，∠ACE＝60°－∠ACD，∴∠BCD＝∠ACE.    在△DBC和△EAC中，∵BC＝AC，∠BCD＝∠ACE，DC＝EC，∴△DBC≌△EAC(SAS)．(2)∵△DBC≌△EAC，∴∠EAC＝∠B＝60°.又∵∠ACB＝60°，∴∠EAC＝∠ACB，∴AE∥BC.12．(1)∠DPC＝20°；(2)∠BAP＝2α－120°.【解析】（1）在△APD中，求得∠PAD的度数，进而求得∠APC的度数，进而即可求解；（2）由（1）解题思路和三角形的内角和定理即可求出∠BAP的度数．解：（1）在△APD中，AP=AD，∴∠APD=∠ADP=80°∴∠PAD=180°-80°-80°=20°∴∠BAP=60°-20°=40°∴∠APC=∠B+∠BAP=60°+40°=100°∴∠DPC=∠APC-∠APD=100°-80°=20°．（2）∵在△APD中，AP=AD，∴∠APD=∠ADP=α°∴∠PAD=180°-α°-α°=180°-2α°∴∠BAP=60°-（180°-2α°）=（2α-120）°.