数学八年级下册2 直角三角形获奖ppt课件

这是一份数学八年级下册2 直角三角形获奖ppt课件，共25页。PPT课件主要包含了新知导入，新知讲解，是直角三角形，几何语言，在Rt△ABC中，∵∠C90°，在△ABC中，它们都是真命题吗，互逆定理，课堂练习等内容，欢迎下载使用。

1.什么是直角三角形？
有一个内角是直角的三角形叫做直角三角形.
2.直角三角形的两个锐角有怎样的关系？
直角三角形的两个锐角互余.
想一想：直角三角形的两个锐角为什么互余呢？
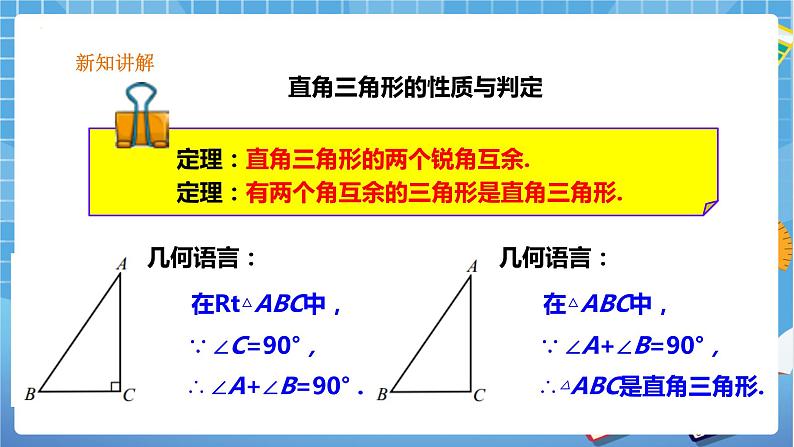
已知：如图所示，在Rt△ABC中，∠C＝90°.求证： ∠A +∠B＝90°.
证明：在Rt△ABC中，∵∠A +∠B+∠C＝90°. 又∵∠C＝90°，∴ ∠A +∠B＝90°. 即：直角三角形的两个锐角互余.
思考：如果一个三角形有两个角互余，那么这个三角形是直角三角形吗？为什么？
已知：如图所示，在△ABC中，∠A +∠B＝90°. 求证：△ABC是直角三角形
证明：在△ABC中，∵∠A +∠B+∠C＝90°. 又∵∠A +∠B＝90°，∴ ∠C＝90°. ∴△ABC是直角三角形.即：有两个角互余的三角形是直角三角形.
直角三角形的性质与判定
定理：直角三角形的两个锐角互余.定理：有两个角互余的三角形是直角三角形.
∴ ∠A+∠B=90° .
∵ ∠A+∠B=90°，
∴△ABC是直角三角形.
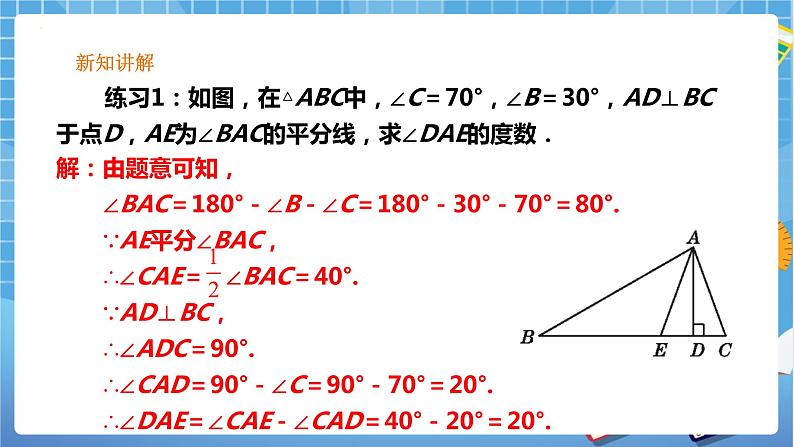
练习1：如图，在△ABC中，∠C＝70°，∠B＝30°，AD⊥BC于点D，AE为∠BAC的平分线，求∠DAE的度数．
解：由题意可知，∠BAC＝180°－∠B－∠C＝180°－30°－70°＝80°.∵AE平分∠BAC，∴∠CAE＝ ∠BAC＝40°.∵AD⊥BC，∴∠ADC＝90°.∴∠CAD＝90°－∠C＝90°－70°＝20°.∴∠DAE＝∠CAE－∠CAD＝40°－20°＝20°.
说一说：在上学期，我们通过数方格和割补法得到了勾股定理，谁能说一说勾股定理的内容呢？
勾股定理：直角三角形两条直角边的平方和等于斜边的平方.
∵△ABC直角是三角形，且∠C＝90 ° ，
∴AC 2+BC 2=AB 2.
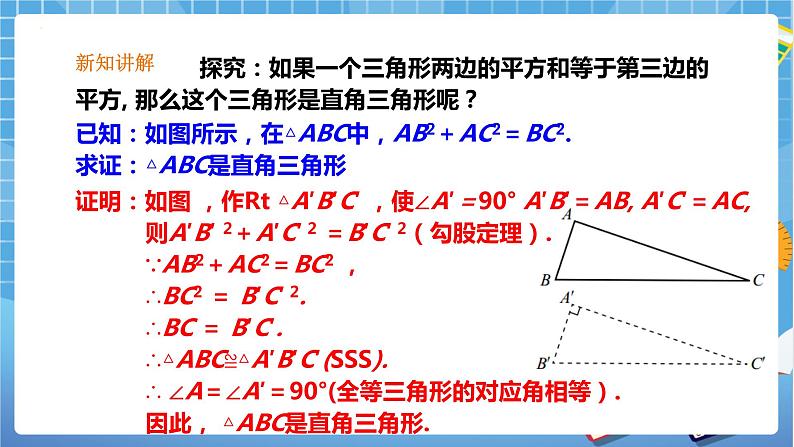
证明：如图 ，作Rt △A′B′C′ ，使∠A′＝90° A′B′＝AB, A′C′＝AC,则A′B′ 2＋A′C′ 2 ＝B′C′ 2（勾股定理）.∵AB2＋AC2＝BC2 ，∴BC2 ＝ B′C′ 2.∴BC ＝ B′C′.∴△ABC≌△A′B′C′(SSS). ∴ ∠A＝∠A′＝90°(全等三角形的对应角相等）.因此， △ABC是直角三角形.
探究：如果一个三角形两边的平方和等于第三边的平方, 那么这个三角形是直角三角形呢？
已知：如图所示，在△ABC中，AB2＋AC2＝BC2.求证：△ABC是直角三角形
定理：如果三角形两边的平方和等于第三边的平方，那么这个三角形是直角三角形.
在△ABC中∵ AC 2+BC 2=AB 2，
∴ △ABC是直角三角形.
练习2：如图，已知∠ABD=90 ° ，AB=8m，AD=17m，DC=20m，BC=25m． （1）求BD的长度；（2）求四边形ABCD的面积．
解：（1）在∴△ABD中，∵∠ABD=90°，∴AB 2+BD 2=AD 2，即：82+BD 2=172，∴BD=15（m）；
解：(2)∵BD=15m，DC=20m，BC=25m，∴BD2+DC2=BC2，∴∠BDC=90°，∴四边形ABCD的面积= AB×BD+ CD×BD= ×8×15+ ×20×15=210(m2) ．
议一议：观察下的两组定理，它们的之间有怎样的关系？
它们的条件和结论交换了位置
再观察下面三组命题：（1）如果两个角是对顶角，那么它们相等； 如果两个角相等，那么它们是对顶角.（2）如果小明患了肺炎，那么他一定会发烧； 如果小明发烧，那么他一定患了肺炎.（3）一个三角形中相等的边所对的角相等； 一个三角形中相等的角所对的边相等.每组中两个命题的条件和结论也有类似的关系吗？
在两个命题中，如果一个命题的条件和结论分别 是另一个命题的结论和条件，那么这两个命题称为互逆命题，其中一个命题称为另一个命题的逆命题．
你能写出命题“如果两个有理数相等,那么它们的平方相等”的逆命题吗?
如果两个有理数的相等平方相等,那么这两个有理数相等.
第一个命题是真命题，它的逆命题是假命题.
一个命题是真命题，它的逆命题不一定是真命题.
判断一个命题是真命题需要进行逻辑推理，判断一个命题是假命题只需要举反例就可以．
如果一个定理的逆命题经过证明是真命题，那么它也是一个定理，其中一个定理称为另一个定理的逆定理，这两个定理称为互逆定理．
练习3：说出下列命题的逆命题，并判断每对命题的真假：(1)五边形是多边形；(2)两直线平行，内错角相等.
解：(1)逆命题：多边形是五边形， 原命题是真命题，逆命题是假命题；(2)逆命题：内错角相等，两直线平行， 原命题是真命题，逆命题也是真命题．
1．一个三角形三个内角的度数之比为1：2：3，则这个三角形一定是(　　)A．锐角三角形 B．直角三角形C．钝角三角形 D．等腰直角三角形
2．已知下列命题：①若 >1，则a>b；②若a＋b＝0，则|a|＝|b|；③等边三角形的三个内角都相等；④底角相等的两个等腰三角形全等．其中原命题与逆命题均为真命题的个数是(　　)A．1个 B．2个 C．3个 D．4个
已知：在△ABC中，AB＝13cm，BC＝10cm，BC边上的中线AD＝12cm. 求证：AB＝AC.
证明： ∵ AD是BC边上的中线，∴ BD＝ BC＝ ×10＝5(cm)．在△ABD中，∵ AB＝13 cm，AD＝12 cm，BD＝5 cm，∴ AB2＝AD2＋BD2.∴ △ABD为直角三角形．∴ AD⊥BC.在Rt△ADC中，∴ AB＝AC.
(2018·青岛) 如图，三角形纸片ABC，AB=AC，∠BAC=90°，点E为AB中点．沿过点E的直线折叠，使点B与点A重合，折痕现交于点F．已知EF= ，则BC的长是（　　）
1、说一说直角三角形在角上的性质与判定？
性质：直角三角形的两个锐角互余.判定：有两个角互余的三角形是直角三角形.
2、说一说直角三角形在边上的性质与判定？
性质：勾股定理：直角三角形两条直角边的平方和等于斜边的平方.
判定： 勾股定理的逆定理：如果三角形两边的平方和等于第三边的平方，那么这个三角形是直角三角形.
3、什么是互逆命题、互逆定理？
在两个命题中，如果一个命题的条件和结论分别 是另一个命题的结论和条件，那么这两个命题称为互逆命题，其中一个命题称为另一个命题的逆命题．
课题：1.2直角三角形（1） 
1、直角三角形的性质与判定2、勾股定理及逆定理3、互逆命题4、互逆定理