初中数学北师大版八年级下册4 角平分线优秀巩固练习

这是一份初中数学北师大版八年级下册4 角平分线优秀巩固练习，共8页。
一．选择题（共5小题，每题8分）
1．在Rt△ABC中，∠C＝90°，D为BC上一点，要使点D到AB的距离等于DC，则必须满足（ ）
A．点D是BC的中点B．点D在∠BAC的平分线上
C．AD是△ABC的一条中线D．点D在线段BC的垂直平分线上
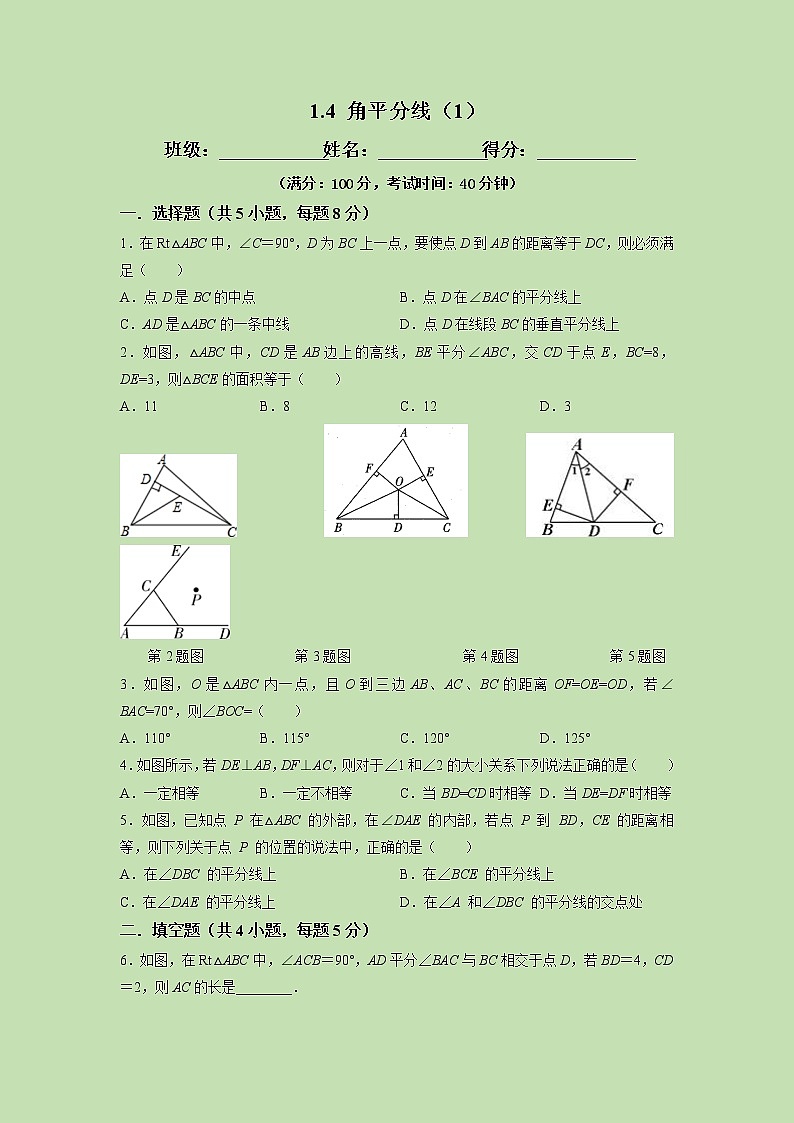
2．如图，△ABC中，CD是AB边上的高线，BE平分∠ABC，交CD于点E，BC=8，DE=3，则△BCE的面积等于（ ）
A．11 B．8 C．12 D．3

第2题图 第3题图 第4题图 第5题图
3．如图，O是△ABC内一点，且O到三边AB、AC、BC的距离OF=OE=OD，若∠BAC=70°，则∠BOC=（ ）
A．110° B．115° C．120° D．125°
4．如图所示，若DE⊥AB，DF⊥AC，则对于∠1和∠2的大小关系下列说法正确的是（ ）
A．一定相等 B．一定不相等 C．当BD=CD时相等D．当DE=DF时相等
5．如图，已知点 P 在△ABC 的外部，在∠DAE 的内部，若点 P 到 BD，CE 的距离相 等，则下列关于点 P 的位置的说法中，正确的是（ ）
A．在∠DBC 的平分线上 B．在∠BCE 的平分线上
C．在∠DAE 的平分线上 D．在∠A 和∠DBC 的平分线的交点处
二．填空题（共4小题，每题5分）
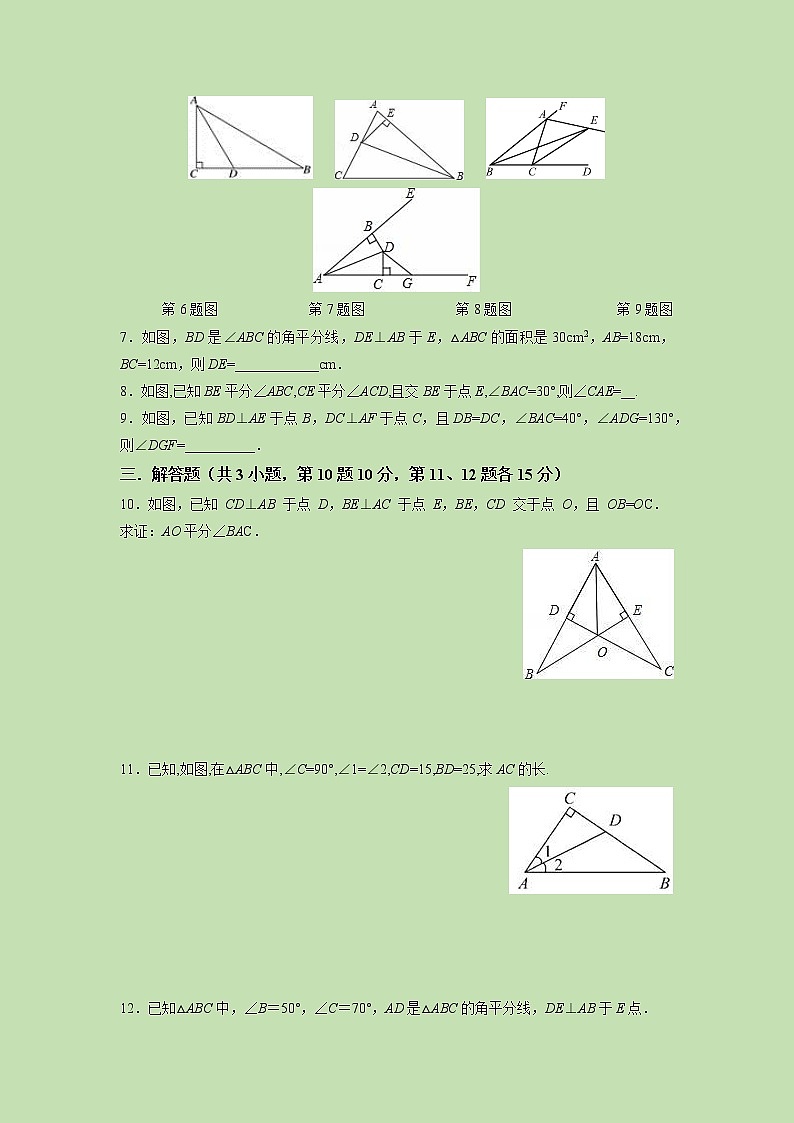
6．如图，在Rt△ABC中，∠ACB＝90°，AD平分∠BAC与BC相交于点D，若BD＝4，CD＝2，则AC的长是________．

第6题图 第7题图 第8题图 第9题图
7．如图，BD是∠ABC的角平分线，DE⊥AB于E，△ABC的面积是30cm2，AB=18cm，BC=12cm，则DE=____________cm．
8．如图,已知BE平分∠ABC,CE平分∠ACD,且交BE于点E,∠BAC=30°,则∠CAE=__.
9．如图，已知BD⊥AE于点B，DC⊥AF于点C，且DB=DC，∠BAC=40°，∠ADG=130°，则∠DGF=__________．
三．解答题（共3小题，第10题10分，第11、12题各15分）
10．如图，已知 CD⊥AB 于点 D，BE⊥AC 于点 E，BE，CD 交于点 O，且 OB=OC．
求证：AO平分∠BAC．
11．已知,如图,在△ABC中,∠C=90°,∠1=∠2,CD=15,BD=25,求AC的长.
12．已知△ABC中，∠B＝50°，∠C＝70°，AD是△ABC的角平分线，DE⊥AB于E点．
（1）求∠EDA的度数；
（2）AB＝10，AC＝8，DE＝3，求S△ABC．
试题解析
1．B
【解析】根据角平分线的判定定理解答即可．
解：如图所示，DE为点D到AB的距离．
∵DC＝DE，∠C＝90°，DE⊥AB，
∴AD平分∠CAD，
则点D在∠BAC的平分线上．
故选B．
2．C
【解析】过E作EF⊥BC于F，根据角平分线性质得出EF=DE=3，根据三角形的面积公式求出即可．
解：过E作EF⊥BC于F，
∵CD是AB边上的高线，BE平分∠ABC，DE=3，
∴EF=DE=3，
∴△BCE的面积S=12×BC×EF=12×8×3＝12，
故选：C．
3．D
【解析】根据在角的内部到角的两边距离相等的点在角的平分线上判断出OB、OC分别平分∠ABC和∠ACB，再根据三角形的内角和定理求出∠ABC＋∠ACB，然后求出∠OBC＋∠OCB，再次利用三角形的内角和定理列式计算即可得解．
解：∵OF＝OD＝OE，
∴OB、OC分别平分∠ABC和∠ACB，
∵∠BAC＝70°，
∴∠ABC＋∠ACB＝180°－70°＝110°，
∴∠OBC＋∠OCB＝12(∠ABC＋∠ACB)＝12×110°＝55°，
∴∠BOC＝180°－(∠OBC＋∠OCB)＝180°－55°＝125°.
故答案为：D.
4．D
【解析】已知有点到∠BAC的两边的距离，根据角平分线性质的逆定理：到角的两边距离相等的点在角的平分线上，要满足∠1=∠2，须有DE=DF，于是答案可得．
解：根据到角的两边距离相等的点在角的平分线上，
故选D．
5．C
【解析】利用平分线性质的逆定理分析．由已知点 P 到 BD，CE 的距离相等进行思考可得出结论．
解： ∵点 P 到 BD，CE 的距离相等,
∴点P在∠DAE 的平分线上,
无法证明在其余角的角平分线上.
故选C.
6．23
【解析】作DE⊥AB于E，根据角平分线的性质得到DE=DC，根据勾股定理求出BE，再根据勾股定理计算即可．
解：作DE⊥AB于E，
∵AD是∠BAC的平分线，∠ACB＝90°，DE⊥AB，
∴DE＝DC＝2，
∴AC＝AE，
由勾股定理，得BE＝BD2-DE2＝23，
设AC＝AE＝x，
由勾股定理，得x2＋62＝(x＋23)2，
解得x＝23.
故答案为：23.
7．2
【解析】作DF⊥BC，由BD是∠ABC的角平分线知DE=DF，再利用△ABC的面积等于△ABD的面积与△BCD的面积之和求解即可.
解：如图作DF⊥BC，∵BD是∠ABC的角平分线，DE⊥AB
∴DE=DF，
设DE=x,
∵S△ABC=S△ABD+S△BCD,
即30=12AB×DE+12BC×DF,
30=12×18x +12×12x,
解得x=2，即DE=2.
8．75°
【解析】如图过点E分别作EG⊥BD、EH⊥BA、EI⊥AC，垂足分别为G、H、I，根据角平分线的性质可得EH=EG，EI=EG，再根据角平分线的性质的逆定理可证AE平分∠FAC，再根据∠FAC与∠BAC互补即可．
证明：如图所示：过点E分别作EG⊥BD、EH⊥BA、EI⊥AC，垂足分别为G、H、I，
∵BE平分∠ABC，EG⊥BD，EH⊥BA，
∴EH=EG．
∵CE平分∠ACD，EG⊥BD，EI⊥AC，
∴EI=EG，
∴EI=EH，
∵EH⊥BA，EI⊥AC，
∴AE平分∠FAC
∵∠BAC=30°
∴∠FAC=180°-∠BAC=150°
∴∠CAE=12∠FAC=75°
故答案为：75°
9．150°
【分析】先根据到角的两边距离相等的点在角的平分线上得到AD是∠BAC的平分线，求出∠CAD的度数，再根据三角形的一个外角等于与它不相邻的两个内角的和即可求解．
解：∵BD⊥AE于B，DC⊥AF于C，且DB=DC，
∴AD是∠BAC的平分线，
∵∠BAC=40°，
∴∠CAD=12∠BAC=20°，
∴∠DGF=∠CAD+∠ADG=20°+130°=150°．
故答案为：150°
10．详见解析.
【解析】根据已知条件证明△BOD≌△COE（AAS），再利用全等三角形性质即可解题.
解：证明：∵CD⊥AB，BE⊥AC，
∴∠BDO=∠CEO=90°，
在△BOD 和△COE 中，
∴△BOD≌△COE（AAS），
∴OD=OE，
∴点 O 在∠BAC 的平分线上， 即 AO 平分∠BAC．
11．AC=30.
【解析】过D作DE⊥AB,垂足为E，利用AD为∠CAB的角平分线得CD=DE，再证Rt△ACD≌Rt△AED,得AC=AE，然后在Rt△ABC中利用勾股定理求出AC即可.
解：过D作DE⊥AB,垂足为E,

∵∠1=∠2,
∴CD=DE=15,
在Rt△BDE中,BE=252-152=20,
∵CD=DE,AD=AD,
∴Rt△ACD≌Rt△AED,
∴AC=AE.
在Rt△ABC中,由勾股定理得AB2=AC2+BC2,
即(AC+20)2=AC2+(15+25)2,
解得AC=30.
12．（1）60°；（2）27.
【解析】（1）先求出∠BAC＝ 60°，再用AD是△ABC的角平分线求出∠BAD，再根据垂直，即可求解；（2）过D作DF⊥AC于F，三角形ABC的面积为三角形ABD和三角形ACD的和即可求解.
解：（1）∵∠B＝50°，∠C＝70°，
∴∠BAC＝180°﹣∠B﹣∠C＝180°﹣50°﹣70°＝60°，
∵AD是△ABC的角平分线，
∴∠BAD＝12∠BAC＝12×60°＝30°，
∵DE⊥AB，
∴∠DEA＝90°，
∴∠EDA＝180°﹣∠BAD﹣∠DEA＝180°﹣30°﹣90°＝60°；