初中数学北师大版八年级下册3 中心对称完整版课件ppt

这是一份初中数学北师大版八年级下册3 中心对称完整版课件ppt，共23页。PPT课件主要包含了新知导入，新知讲解，观察图2再试一试，中心对称的定义，中心对称的性质，3－1，轴对称，中心对称，中心对称图形，平行四边形等内容，欢迎下载使用。

1、观察下面图形，它们都属于什么图形？
答：它们都是轴对称图形
2、什么是轴对称图形？
如果一个平面图形沿一条直线折叠后，直线两旁的部分能够互相重合，那么这个图形叫做轴对称图形，这条直线叫做对称轴.
观察：如图1所示，图（1）经过怎样的运动变化就可以与图（2）重合？
如果把一个图形绕着某一点旋转180°，它能够与另一个图形重合，那么就说这两个图形关于这个点对称或中心对称.这个点叫做它们的对称中心.
注意：中心对称不改变图形的形状和大小.
中心对称也是一种全等变换
“两个图形关于一个点对称”可以简称为“两个图形成中心对称”.
练习1：下列各组图形中，右边的图形与左边的图形成中心对称的是(　　)
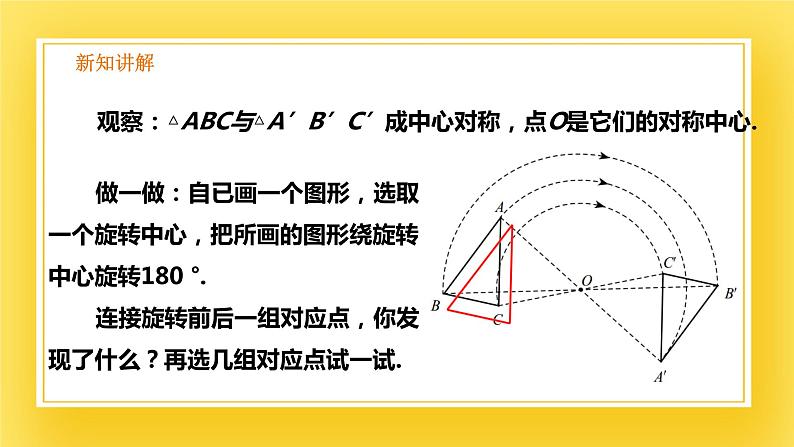
观察：△ABC与△A’B’C’成中心对称，点O是它们的对称中心.
做一做：自已画一个图形，选取一个旋转中心，把所画的图形绕旋转中心旋转180 °.连接旋转前后一组对应点，你发现了什么？再选几组对应点试一试.
成中心对称的两个图形中，对应点所连线段经过对称中心，且被对称中心平分.
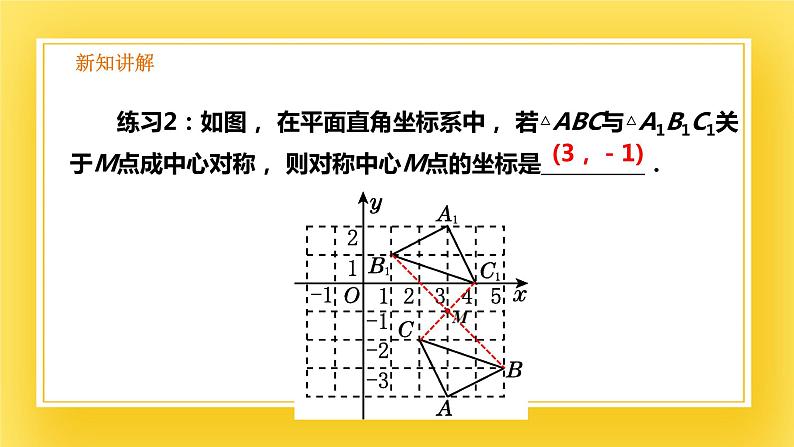
练习2：如图， 在平面直角坐标系中， 若△ABC与△A1B1C1关于M点成中心对称， 则对称中心M点的坐标是__________．
中心对称与轴对称的联系与区别
翻转后和另一个图形重合
旋转后和另一个图形重合
试一试：你能利用中心对称的性质画出一个图形关于某个点成中心对称的图形吗？
例：如图所示，点O 是线段AE 的中点，以点O 为对称中心，画出五边形ABCDE 成中心对称的图形.
解：如图, 连接BO并延长至B′，使得OB′ =OB ;连接CO并延长至C'，使得OC′ =OC ;连接DO并延长至D′，使得OD′ =OD ; 顺次连接A, D′, C′, B′,E.图形AD′C′B′E 就是以点O为对称中心、与五边形ABCDE成中心对称的图形.
（1）连接原图形上的关键点和对称中心；（2）再将以上各线段延长找对称点，使得关键点与对称中心的距离和其对称点与对称中心的距离相等；（3）将对称点按原图形的形状连接起来，即可得出原图形关于某点中心对称的图形．
说一说：画已知图形关于某个点成中心对称的图形的步骤.
练习3：如图，点O是△ABC外一点，画△A′B′C′，使△A′B′C′与△ABC关于点O成中心对称.
解：△ A’B’C’如图所示.
议一议：下面这些图形有什么共同特征？你还能举出一些类似的图形吗？
把一个图形绕着某一点旋转180°，如果旋转后的图形能与原来的图形重合，那么这个图形叫做中心对称图形.这个点叫做它的对称中心.
议一议：（1）在你所学过的平面图形中，哪些图形是中心对称图形？
（2）在上面的例题中，图形ABCDEB′ C′D′ 是中心对称图形？
中心对称与中心对称图形的联系与区别
区别: 中心对称指两个全等图形的相互位置关系,中心对称图形指一个图形本身成中心对称.
联系: 如果将中心对称图形的两个图形看成一个整体,则它们是中心对称图形.
如果将中心对称图形对称的部分看成两个图形,则它们成中心对称.
1．如图，在平行四边形ABCD中，对角线AC，BD相交于点O，则与△AOB成中心对称的三角形是(　　)A．△BOC B．△COD C．△AOD D．△ACD
2．如图，四边形ABCD与四边形FGHE关于一个点成中心对称，则这个点是(　　)A．O4 B．O3 C．O2 D．O1
在平面直角坐标系中，点P(－3，－5)关于原点对称的点的坐标是(　　)A．(3，－5) B．(－3，5)C．(3，5) D．(－3，－5)
两个点关于原点对称时，它们的坐标符号相反. 即：点P（x，y）关于原点的对称点为P’（-x，-y）
如果把一个图形绕着某一点旋转180°，它能够与另一个图形重合，那么就说这两个图形关于这个点对称或中心对称.
2、中心对称的性质是什么？
3、什么是中心对称图形？
把一个图形绕着某一点旋转180°，如果旋转后的图形能与原来的图形重合，那么这个图形叫做中心对称图形.
成中心对称的两个图形全等.
课题：3.3 中心对称 
一、中心对称二、中心对称的性质三、中心对称图形