初中数学北师大版八年级下册2 平行四边形的判定优秀课件ppt

这是一份初中数学北师大版八年级下册2 平行四边形的判定优秀课件ppt，共21页。PPT课件主要包含了复习回顾，新知讲解，证明连接BD，证明连接AC，∵AD∥BC，∴∠DAC∠ACB，∴ΔABC≌ΔCDA，∴∠BAC∠ACD，∴AB∥CD，数学语言表示为等内容，欢迎下载使用。

1．平行四边形的定义是什么？2．平行四边形的性质有哪些？
平行四边形的对边平行且相等平行四边形的对角相等，邻角互补平行四边形的对角线互相平分
两组对边分别平行的四边形是平行四边形。
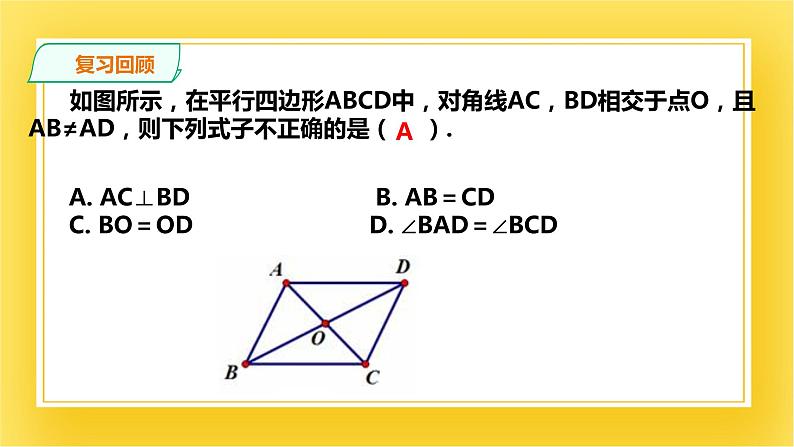
如图所示，在平行四边形ABCD中，对角线AC，BD相交于点O，且AB≠AD，则下列式子不正确的是（　 ）. 　　　　　　　　　　　　　　　　
　　A. AC⊥BD　　　　　　　　B. AB＝CD　　 　　C. BO＝OD　　　　　 　　 D. ∠BAD＝∠BCD 　
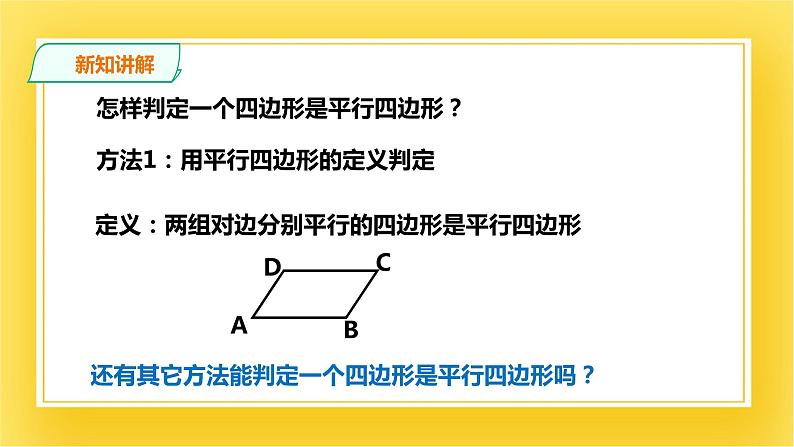
怎样判定一个四边形是平行四边形？
方法1：用平行四边形的定义判定
定义：两组对边分别平行的四边形是平行四边形
还有其它方法能判定一个四边形是平行四边形吗？
活动探究一：做一做 :小组活动，回答下列问题。（小组讨论，3min）
活动：工具:四根细木条，其中两根长度相同，另外两根长度也相同动手:能否合理摆放这四根细木条,使得连接四个顶点后成为平行四边形？思考：你能说明你得到的四边形是平行四边形吗？
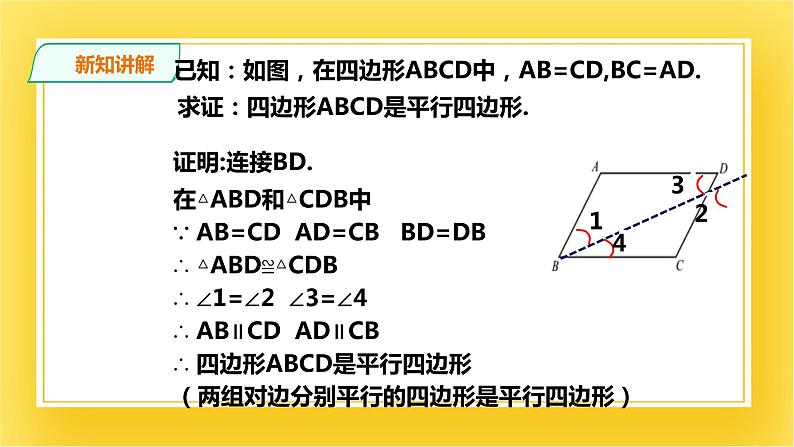
已知：如图，在四边形ABCD中，AB=CD,BC=AD.
∴ 四边形ABCD是平行四边形
在△ABD和△CDB中
∵ AB=CD AD=CB BD=DB
∴ △ABD≌△CDB
∴ ∠1=∠2 ∠3=∠4
∴ AB∥CD AD∥CB
求证：四边形ABCD是平行四边形.
（两组对边分别平行的四边形是平行四边形）
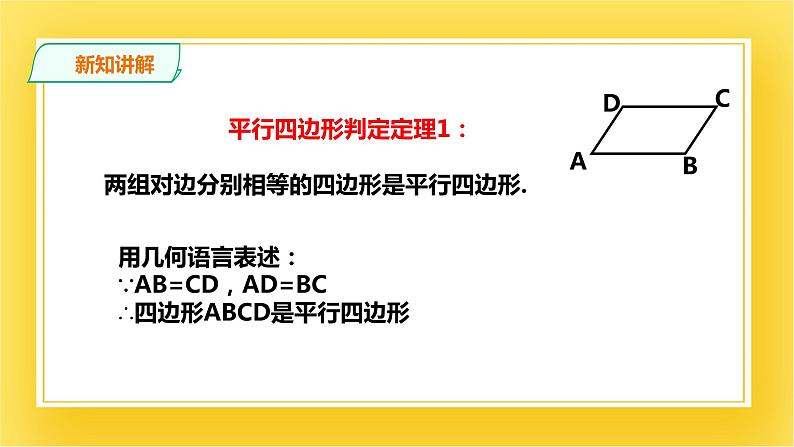
平行四边形判定定理1： 两组对边分别相等的四边形是平行四边形.
用几何语言表述：∵AB=CD，AD=BC∴四边形ABCD是平行四边形
工具: 两根长度相等的线段.动手:1.利用两根长度相等的线段，能摆出以线段端点为顶点的平行四边形吗?3.利用两根长度相等的线段和两条平行线,能摆出以线段端点为顶点的平行四边形吗?
猜想：一组对边平行且相等的四边形是平行四边形
思考：你能说明你所摆出的四边形是平行四边形吗？
活动探究二：做一做 :小组活动，回答下列问题。（小组讨论，3min）
求证：四边形ABCD是平行四边形。
又∵AD=BC，AC=CA
∴四边形ABCD是平行四边形（ 平行四边形的定义）
∵ AD=BC，AD∥BC （已知） ∴四边形ABCD是平行四边形（一组对边平行且相等的四边 形是平行四边形。）
一组对边平行且相等的四边形是平行四边形
平行四边形的判定定理2:
例1 如图6-10，在平行四边形ABCD中，E、F分别是AD和BC的中点．求证：四边形BFDE是平行四边形.
∴ 四边形BFDE是平行四边形
证明：∵ 四边形ABCD是平行四边形
∴ AD=CB AD//BC
又∵E、F分别是AD和BC的 中点
已知,如图,在平行四边形ABCD中,E,F分别是边AD,BC的中点. 求证:EB=DF
证明: ∵ ABCD是平行四边形 ∴ AD=BC AD//BC ∵E,F分别是边AD,BC的中点 ED=1/2AD BF=1/2BC ∴ED=BF,且ED//BF ∴四边形BFDE是平行四边形∴ EB=DF
变式1：在下列条件中,不能判定四边形是平行四边形的是( )AB=CD,AD∥BC AB=CD,AB ∥CD (C)AB∥CD, AD∥BC (D) AB=CD,AD=BC
变式2：已知：四边形ABCD, ∠A=∠C，∠B=∠D求证：四边形ABCD是平行四边形
∴四边形ABCD是平行四边形(两组对边分别平行的四边形是平行四边形)
又∵∠A+ ∠B+ ∠C+ ∠D =360 °
∴ 2∠A+ 2∠B=360 °
∵∠A=∠C，∠B=∠D（已知）
即∠A+ ∠B=180 °
∴ AD∥BC （同旁内角互补，两直线平行）
已知：如图，AD⊥AC,BC⊥AC,且AB=CD.求证：AB∥CD.
∵AD⊥AC, BC⊥AC,
∴AD∥BC, ∠BCA=∠DAC=90O,
又∵AB=CD, AC=CA,
∴Rt⊿ACB≌Rt⊿CAD.
∴四边形ABCD是平行四边形（一组对边平行且相等的四边形是平行四边形）。
∴AB∥CD(平行四边形的定义)。
如图，在平形四边形ABCD中，AB＝3，AD＝4，∠ABC＝60°，过BC的中点E作EF⊥AB，垂足为点F，与DC的延长线相交于点H，则△DEF的面积是__________.
1、两组对边分别平行的四边形是平行四边形。
2、两组对边分别相等的四边形是平行四边形。
3、一组对边平行且相等的四边形是平行四边形。
判定一个四边形是平行四边形的方法：
定义、两组对边分别平行的四边形是平行四边形。定理1、两组对边分别相等的四边形是平行四边形。定理2、一组对边平行且相等的四边形是平行四边形。
6.2.1 平行四边形的判定（一）
1、已知：如图，CD是线段AB经平移所得的像，连结AD,BC. 求证：四边形ABCD是平行四边形。
　2、如图所示，E、F分别为四边形ABCD的边AD、BC上的点，且四边形AECF和DEBF都是平行四边形，AF和BE相交于点G，DF和CE相交于点H．求证：四边形EGFH为平行四边形．