数学八年级下册第六章 平行四边形4 多边形的内角与外角和获奖教案设计

这是一份数学八年级下册第六章 平行四边形4 多边形的内角与外角和获奖教案设计，共4页。


课题
6.4.2 多边形内角和与外角和(二)
单元
第六章第4节第2课时
学科
数学
年级
八年级下
教材分析
《多边形内角和》选自北师大版义务教育教科书《数学》八年级下册第六章第四节《多边形及内角和与外角和》的第2课时。通过这节课的学习，可以培养学生积极参与的习惯及探索与归纳的能力，体会从简单到复杂，从特殊到一般，以及类比，转化等重要的数学思想方法。
学情分析
学生在上节课已经学习了求多边形的内角和的方法，这为本节课的学习打下了一定的基础。通过多边形外角和定理的推导,感悟“从特殊到一般”的“化归”思想，激发学生学习兴趣，培养学生合作的团队精神.
学习
目标
（1）经历探索多边形的外角和公式的过程;会应用公式解决问题；
（2） 培养学生把未知转化为已知进行探究的能力，在探究活动中，进一步发展学生的说理能力与简单的推理能力．
（3）让学生体验猜想得到证实的成功喜悦和成就感，在解题中感受生活中数学的存在，体验数学充满着探索和创造．
重点
多边形外角和定理的探索和应用．
难点
灵活运用公式解决简单的实际问题；转化的数学思维方法的渗透．
教学过程
教学环节
教师活动
学生活动
设计意图
导入新课
1、多边形的内角和公式是什么?
2、正n边形的内角怎么计算？
老师提问并解答问题；
通过设立悬念进入新课
复习旧知识，导入新知识。
讲授新课
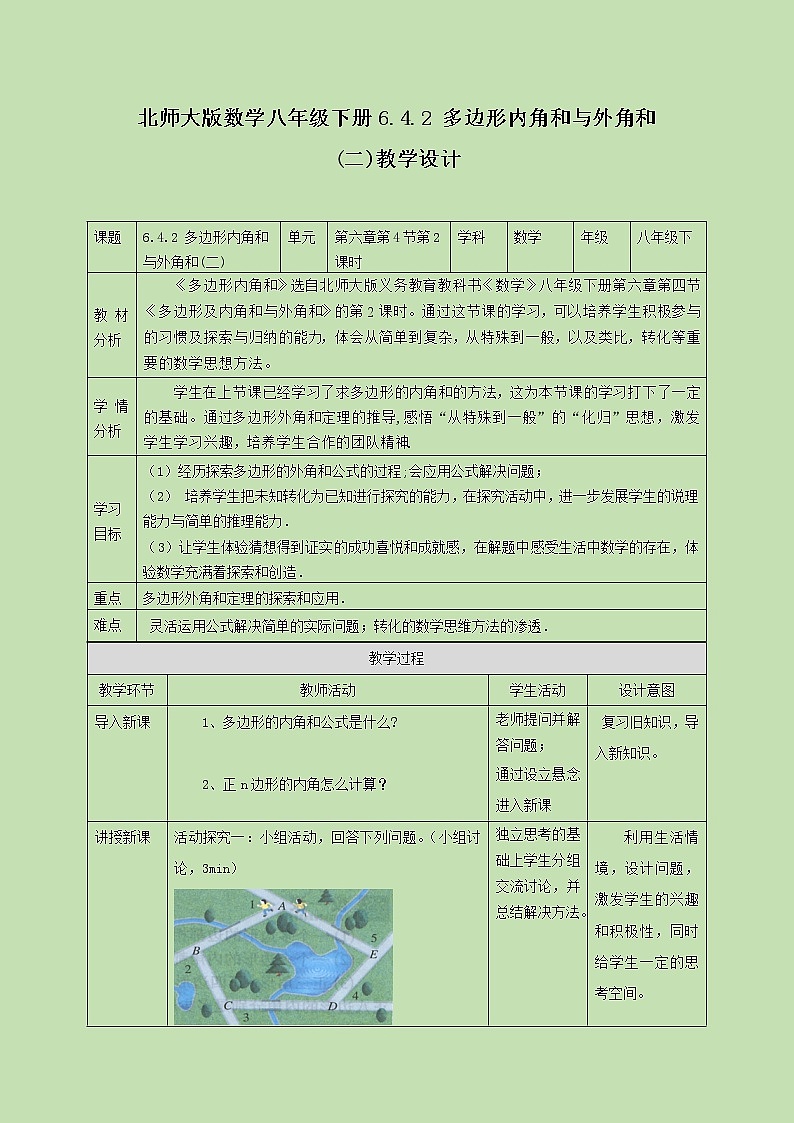
活动探究一：小组活动，回答下列问题。（小组讨论，3min）
（1）小刚每从一条小路转到下一条小路时，跑步方向改变的角是哪个角？
（2）他每跑完一圈，身体转过的角度之和是多少？
（3）在下图中，你能求出1+2+3+4+5的结果吗？你是怎样得到的？
∵∠1+∠EAB=1800
∠2+∠ABC=1800
∠3+∠BCD=1800
∠4+∠CDE=1800
∠5+∠DEA=1800
∴ ∠1+∠EAB+ ∠2+∠ABC+∠3+∠BCD+ ∠4+∠CDE+ ∠5+∠DEA=9000
∵五边形的内角和为（5-2）×1800=5400
∠δ，∠θ，其中，∠α=∠1，∠β=∠2，∠γ=∠3，∠δ=∠4，∠θ=∠5．
这样，∠1+∠2+∠3+∠4+∠5=360°
【想一想】如果广场的形状是六边形、八边形，那么还有类似的结论吗？
多边形内角的一边与另一边的反向延长线所组成的角叫做这个多边形的外角.
在每个顶点处取这个多边形的一个外角，它们的和叫做这个多边形的外角和.
则根据题意，
得（n-2）﹒180°=3×360°
解得n=8
所以这个多边形是八边形。
变式1：下列命题是假命题的是（ ）
A.三角形的内角和是180°．
B.多边形的外角和都等于360°．
C.五边形的内角和是900°．
D.三角形的一个外角等于和它不相邻的两个内角的和．
变式2： 正五边形的每一个外角等于____，每一个内角等于_____。
变式3：一大门的栏杆如图所示，BA垂直于地面AE于A，CD平行于地面AE，则∠ABC+∠BCD＝ 度．
拓展提高：
已知一个多边形，它的内角和等于外角和的2倍，求这个多边形的边数。
作业布置：
1.如果十二边形的每一个内角都相等，那么每个内角是_______度.
2.若正n边形的一个内角是144度，则n=______.
必做题：课本P156 随堂练习
选做题：课本P157 习题6.8中1、2题
独立思考的基础上学生分组交流讨论，并总结解决方法。
通过问题的解决和延伸，引发学生自主思考，由特殊到一般，培养学生解决问题的逻辑思维能力，也为多边形外角和的得出做好铺垫。
利用生活情境，设计问题，激发学生的兴趣和积极性，同时给学生一定的思考空间。
通过问题的解决和延伸，引发学生自主思考，由特殊到一般，培养学生解决问题的逻辑思维能力，也为多边形外角和的得出做好铺垫。
课堂小结
1.多边形的外角及外角和的定义
多边形内角的一边与另一边的反向延长线所组成的角叫做这个多边形的外角.
在每个顶点处取这个多边形的一个外角，它们的和叫做这个多边形的外角和.
2.多边形的外角和等于360°
学生总结
老师对学生的总结点评
总结对本节课的收获和体会，自主构建知识体系，锻炼学生的口头表达能力，培养学生的自信能心。
板书
6.4.2多边形内角和与外角和（二）
1.多边形的外角及外角和的定义
2.多边形的外角和等于360°