沪科版17.5 一元二次方程的应用优质课件ppt

这是一份沪科版17.5 一元二次方程的应用优质课件ppt，文件包含175一元二次方程的应用ppt、175一元二次方程的应用教学设计doc、175一元二次方程的应用同步练习doc等3份课件配套教学资源，其中PPT共31页， 欢迎下载使用。

解一元二次方程有哪些方法？
直接开平方法配方法公式法因式分解法
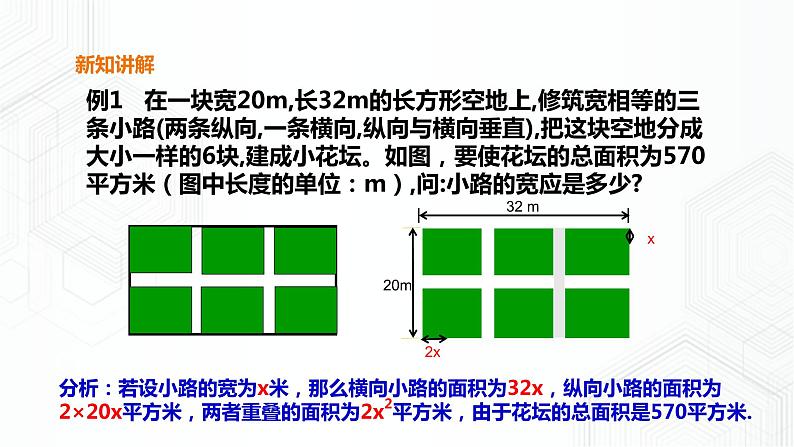
例1 在一块宽20m,长32m的长方形空地上,修筑宽相等的三条小路(两条纵向,一条横向,纵向与横向垂直),把这块空地分成大小一样的6块,建成小花坛。如图，要使花坛的总面积为570平方米（图中长度的单位：m）,问:小路的宽应是多少?
分析：若设小路的宽为x米，那么横向小路的面积为32x，纵向小路的面积为2×20x平方米，两者重叠的面积为2x2平方米，由于花坛的总面积是570平方米.
解:设小路的宽是xm，根据题意，得
结合题意，x=35不可能，因此，只能取x=1.
答:所求小路的宽应为1m.
注意：在解方程时，注意解法。并且根据实际问题考虑方程根的取舍。
图形面积的转化： 平移转化是列一元二次方程解决面积类应用题常用的方法。其核心思想是将不在一起的几块图形通过平移转化为一块规则的图形，然后根据面积列出一元二次方程。
例2　原来每盒27元的一种药品，经两次降价后每盒售价为9元。求该药品两次降价的平均降价率是多少？（精确到1﹪）
解：设两次降价的平均降价率是x，
根据题意，得： 27·（1-x）2 = 9 （1-x）2 ≈ 0.3333 1-x ≈ ± 0.5773 1-x ≈ 0.5773 或 1+x ≈–0.5773 x1 ≈ 0.4227 x2 ≈1.5773(舍去)答；两次降价的平均降价率约为42% .
连续两次增长（或降低）的形式：
2.如果设平均每次降低的百分数为x，原产值（基数）a 经过两次降低到 b ， 可列出关系式为：
a（1+ x） 2 = b
1.如果设平均每次增长的百分数为x，原产值（基数）a 经过两次增长到 b ， 可列出关系式为：
a（1- x） 2 = b
第n次增长后的量是a(1+x)n=b，这就是重要的增长率公式.
注意:增长率不可为负，但可以超过1.
分析：设新品种花生产量的增长率为x ，这个新品种花生出油率的增长率为 x ，根据新品种花生每公顷产量×新品种花生出油率＝1980 ，可列出方程，
解：设新品种花生产量的增长率为x ，根据题意得，
3000（1+x)[50%(1+ x)]=1980
x1 =0.2=20%,x2 =-3.2(不符合题意，舍去)
答 ：新品种花生产量的增长率为20% .
注意:在列方程解应用题时，找到关键描述语，找到等量关系，准确列出方程，是解决问题的关键.
例4　正方形金属片一块，将其四个角各截去一个相同大小的小正方形，围成高20厘米，容积为2880立方厘米的开口方盒，问原金属片的边长是多少？
分析：根据图形，有体积公式可得方程，解方程即可.
解：设原金属片的边长为x厘米，则方盒的底边长是（x-40）厘米，
20（x-40)2=2880
x1 =52,x2 =28(不符合题意，舍去)
答 ：原金属片的边长是52厘米.
（x-40)2=144
列方程(组)解应用题的步骤：
①设②审③找④列⑤解⑥验⑦答
审清题意:已知什么,求什么?已、未知之间有什么关系?
语句要完整,有单位(统一)的要注明单位;
如果是分式方程务必要检验
答案也必需是完整的语句,注明单位且要贴近生活.
等量关系是方程的雏形，务必学会从题目里找出等量关系
列一元二次方程解应用题的步骤，与列一元一次方程解应用题的步骤类似，即审、找、列、解、答，这里要特别注意，在列一元二次方程解应用题时，由于所得的根一般有两个，所以要检验这两个根是否符合实际问题的要求.
例5　一组学生组织春游，预计共需费用120元，后来又有两人参加进来，费用不变，这样每人可少分摊3元，问原来这组学生的人数是多少？
分析: 设原来这组学生的人数是 x人,根据问题本身和它的本质,列出下面的关系
等量关系是: 原来每人费用－加人后每人的费用=3元
两边同乘x(x+2),整理得
分解得: ( x+10 )( x －8 )=0
解这个方程,得 x1=-10, x2=8
经检验, x1=-10, x2=8都是原方程的解,但x1=-10不符合应用题实际(学生数不可能为负数),所以取x=8 答：原来这组学生是8人.
对于可化为一元二次方程的分式方程应用题，要根据它的特点，借助适当的方式(列表,示意图,关系式等)合理理解题目意思，规范解题.
1.如图,长方形ABCD,AB=15m,BC=20m,四周外围环绕着宽度相等的小路,已知小路的面积为246m2,求小路的宽度.
解:设小路宽为x米，则
2 有长为24米的篱笆，一面利用墙（墙长a=10米），围成中间隔有一道篱笆的长方形花圃，如果围成面积为45 平方米的花圃，AB的长是多少？
分析：设花圃的宽为x，用总长减去三个宽，即为ＢＣ的长，则ＢＣ＝（24-3x）米，再利用矩形的面积公式列出方程，求解即可，
3.为了响应国家关于抚贫工作的文件精神，某单位开展了对贫困户的捐款活动。第一天收到捐款10000元，第三天收到捐款12100元。(1)如果第二天、第三天收到捐款的增长率相同，求捐 款的增长率；(2)按照( 1)中收到捐款的增长速度，第四天该单位能收到多少捐款？
=10000（1+x）
10000（1+x）x
=10000（1+x）2
解：(1)设捐款的增长率为x，则
(2)方法一：12 100×(1＋10%)=13310(元)．
4.某百货大楼服装柜在销售中发现：“好孩子”牌服装平均每天可售出 20 件，每件盈利 40 元．为了迎接“十一”国庆节，商场决定采取适当的降价措施，扩大销售量，增加盈利，减少库存．经市场调查发现：如果每件童装降价 4 元，那么平均每天就可多售出 8 件．要想平均每天销售这种服装盈利 1200 元，那么每件童装应降价多少元？
解：设每件童装应降价x元，根据题意得（40-x）（20+2x）=1200，∴x1=10，x2=20，根据题意，x1=10不合题意，应取x=20．答：每件童装应降价20元.
为什么取20而不取10呢？
1.(2018安徽）据省统计局发布，2017年我省有效发明专利数比2016年增长22.1%，假定2018年的平均增长率保持不变，2016年和2018年我省有效发明专利分别为a万件和b万件，则（ ）
【分析】根据题意可知2017年我省有效发明专利数为（1+22.1%）a万件，2018年我省有效发明专利数为（1+22.1%）•（1+22.1%）a，由此即可得.
Ａ. b=(1+22.1%×2)aＢ. b=(1+22.1%)2aＣ. b=(1+22.1%) ×2aＤ. b=22.1%×2a
解:由题意得：2017年我省有效发明专利数为（1+22.1%）a万件，2018年我省有效发明专利数为（1+22.1%）•（1+22.1%）a万件，即b=（1+22.1%）2a万件，故选B.
2.(2018宁夏)某企业2018年初获利润300万元，到2020年初计划利润达到507万元.设这两年的年利润平均增长率为x.应列方程是( )A.300（1+x）=507 B.300（1+x）2=507C.300（1+x）+300（1+x）2=507D.300+300（1+x）+300（1+x）2=507
分析:设这两年的年利润平均增长率为x，根据2018年初及2020年初的利润，即可得出关于x的一元二次方程，此题得解．
解：设这两年的年利润平均增长率为x， 根据题意得：300（1+x）2=507． 故选：B．
a(1+x)2 = b其中a为增长前的量，x为增长率，2为增长次数，b为增长后的量.
a(1- x)2 = b其中a为降低前的量，x为降低率，2为降低次数，b为增长后的量，注意1与x位置不可调换.
常见几何图形面积是等量关系
通过今天的学习，你有哪些收获？和同学相互交流。
1.列方程(组)解应用题的步骤：
2.连续两次增长（或降低）的形式：
a(1± x)2 = b
1.必做题：课本45页习题17.5 2、3、4、2.选做题：课本45页习题17.5 5、6