





初中数学沪科版八年级下册18.2 勾股定理的逆定理一等奖课件ppt
展开1.直角三角形有哪些性质?
2.如何判断三角形是直角三角形?
(1)有一个角是90°;
(2)两个锐角的和是90° ;
(1)有一个角为90°的三角形是直角三角形;
(2)如果一个三角形中,有两个角的和是90°,那么这个三角形也是直角三角形.
(3)勾股定理:直角三角形两条直角边的平方和,等于斜边的平方
(4)30°的角所对的直角边等于斜边的一半.
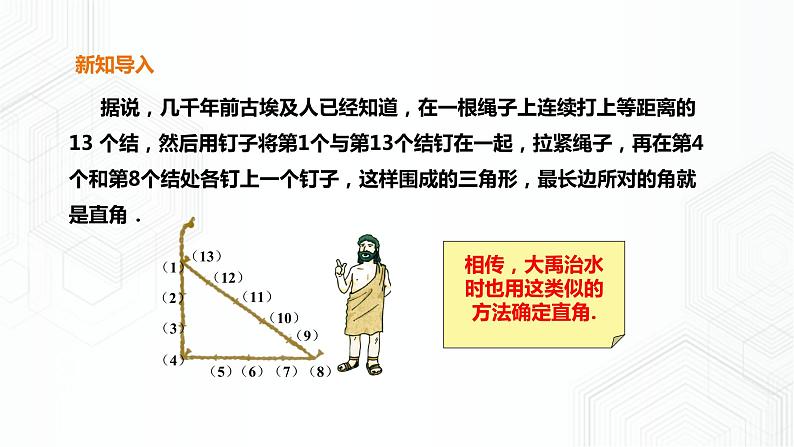
据说,几千年前古埃及人已经知道,在一根绳子上连续打上等距离的13 个结,然后用钉子将第1个与第13个结钉在一起,拉紧绳子,再在第4个和第8个结处各钉上一个钉子,这样围成的三角形,最长边所对的角就是直角.
相传,大禹治水时也用这类似的方法确定直角.
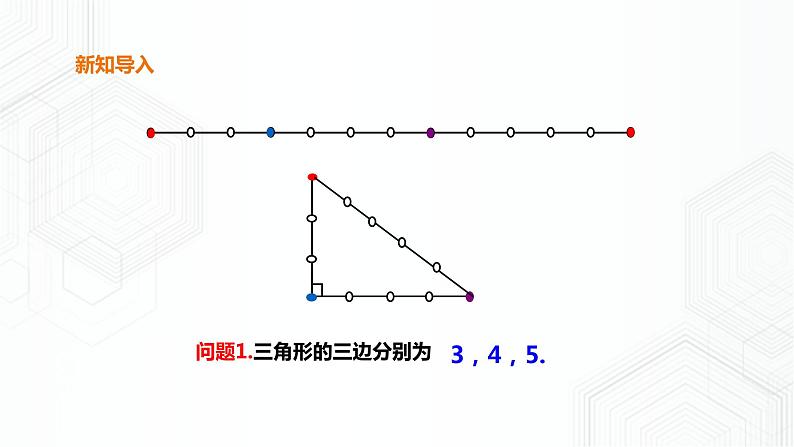
问题1.三角形的三边分别为
实验操作: 分别以这些数为边长画出三角形(单位:cm),它们一定是直角三角形吗? ① 3, 4, 5; ② 6,8,10.
用量角器分别测量上述各三角形的最大角的度数
这三组数都满足a2+b2=c2吗?
如果三角形的三边长a,b,c满足 a2+b2=c2那么这个三角形是直角三角形.
我们发现这个定理可以用来判定一个三角形是直角三角形.
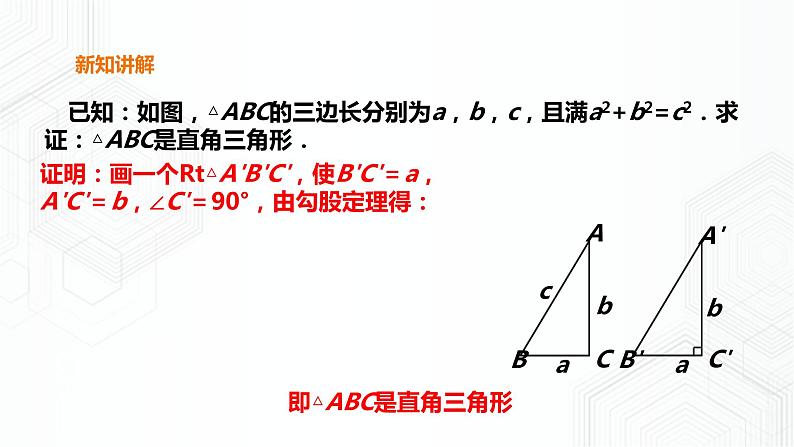
已知:如图,△ABC的三边长分别为a,b,c,且满a2+b2=c2.求证:△ABC是直角三角形.
证明:画一个Rt△A'B'C',使B'C'=a,A'C'=b,∠C'=90°,由勾股定理得:
即△ABC是直角三角形
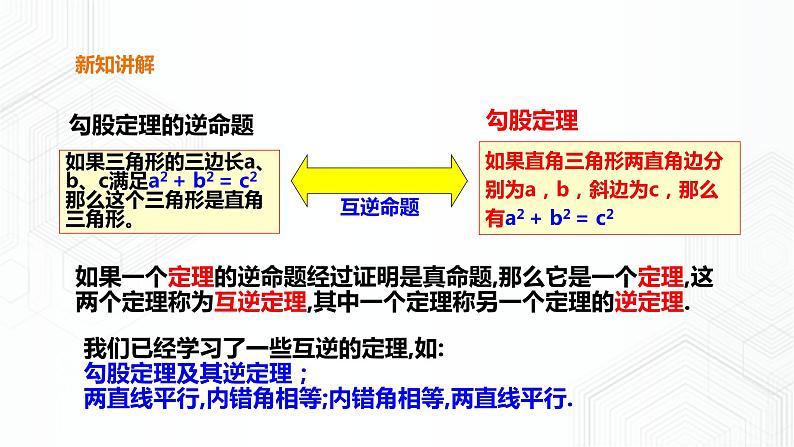
如果直角三角形两直角边分别为a,b,斜边为c,那么有a2 + b2 = c2
如果三角形的三边长a、b、c满足a2 + b2 = c2那么这个三角形是直角三角形。
我们已经学习了一些互逆的定理,如:勾股定理及其逆定理;两直线平行,内错角相等;内错角相等,两直线平行.
如果一个定理的逆命题经过证明是真命题,那么它是一个定理,这两个定理称为互逆定理,其中一个定理称另一个定理的逆定理.
例1 判断由a、b、c组成的三角形是不是直角三角形:(1) a=7 , b =24 , c=25
(2) a=7, b =8 , c=11
分析:由勾股定理的逆定理,判断三角形是不是直角三角形,只要看两条较小边的平方和是否等于最大边的平方。
解: (1) ∵ 最大边是c=25, c2 = 252=625 a2 + b2 =72+242=49+576 =625 ∴ a2 + b2 = c2 ∴ 这个三角形是直角三角形
解:(2) ∵最大边是a=11,a2=121, b2+c2=72+82=113,
∴ △ABC不是直角三角形.
像7、24、25能够成为直角三角形三条边长度的三个正整数,称为勾股数.
例2 下列各组数是勾股数的是( ) A.6,8,10 B.7,8,9 C.0.3,0.4,0.5 D.52,122,132
方法点拨:根据勾股数的定义,勾股数必须为正整数,先排除小数,再计算最长边的平方是否等于其他两边的平方和即可.
分析:先来判断a,b,c三边哪条最长,可以代n为满足条件的特殊值来试,n=4.则a=15,b=8,c=17,c最大.
例3 已知:在△ABC中,三条边长分别为 a=n2 - 1, b=2n,c=n2 +1( n>1,n是正整数), 求证:△ABC为直角三角形.
证明:∵a2+b2=(n2-1)2+(2n)2 =n4-2n2+1+4n2 =n4+2n2+1 =(n2+1)2=c2,
∴ △ABC是直角三角形,(勾股定理的逆定理).
1. 三角形中,大边对 角,小边对 角,直角三角形中的最大角是 ,是 边所对的角.
2. 判定一个三角形是否是直角三角形的步骤有哪些?
(1)找到最大边并计算它的平方,
(2)计算另两边的平方和,
(3)若两数相等,则三角形是直角三角形, 若不相等,则这个三角形不是直角三角形
1.如果线段a,b,c能组成直角三角形,则它们的比可以是 ( )A.3:4:7 B.5:12:13 C.1:2:4 D.1:3:5
分析:根据勾股定理的逆定理,要能组成一个直角三角形的三边应满足:两条较小边的平方和等于最大边的平方.
∵ 52+122=132∴三条线段能组成直角三角形
将直角三角形的三边长扩大同样的倍数,则得到的三角形 ( )A.是直角三角形 B.可能是锐角三角形C.可能是钝角三角形 D.不可能是直角三角形
分析:由于三角形是直角三角形,所以三边满足勾股定理,当各边扩大或者缩小k倍时,再利用勾股定理的逆定理,判断三角形的形状,
设直角三角形的直角边分别是a、b,斜边为c,则满足a2+b2=c2,若各边都扩大k倍,则三边分别是ax、bk、cK,∵ (ax)2+ (bk) 2=k2(a2+b2)= (cK) 2∴三角形为直角三角形
3.三角形三边a,b,c 满足条件:(a+b)2-c2=2ab,此三角形是( )A.锐角三角形B.直角三角形C.钝角三角形D.等边三角形
分析:因为a、b、c,分别为三角形的三边,可化简:(a+b)2-c2=2ab得到结论,
4.以△ABC的三条边为边长向外作正方形, 依次得到的面积是25, 144 , 169, 则这个三角形是 ______三角形.
分析:根据勾股定理的几何意义, 25+ 144= 169,即52+122=132则这个三角形的形状可判定,
∵ 25+ 144= 169 ∴ 52+122=132∴三条线段能组成直角三角形
5.如图,在正方形ABCD中,AB=4,AE=2,DF=1, 图中有几个直角三角形,你是如何判断的? 与你的同伴交流.
解:△ABE,△DEF,△FCB均为直角三角形. 由勾股定理知 BE2=22+42=20,EF2=22+12=5, BF2=32+42=25, ∴BE2+EF2=BF2, ∴ △BEF是直角三角形.
1.(2018南通)下列长度的三条线段能组成直角三角形的是( )A.3,4,5 B.2,3,4 C.4,5,6 D.5,11,12
分析:利用勾股定理的逆定理,如果三角形两条边的平方和等于第三边的平方,那么这个三角形就是直角三角形,最长边所对的角为直角,由此可判定即可,
∵ 32+42=52∴三条线段能组成直角三角形
2.(2017益阳)如图,△ABC中,AC=5,BC=12,AB=13,CD是AB边上的中线.则CD= .
分析:先根据勾股定理的逆定理判定△ABC为直角三角形,然后根据直角三角形的性质即可得到结论.
解:∵在△ABC中,AC=5,BC=12,AB=13,∴AC2+BC2=52+122=132=AB2,∴△ABC为直角三角形,且∠ACB=90°,∵CD是AB边上的中线,∴CD=6.5;故答案为:6.5.
勾股定理的逆定理:如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形是直角三角形.
勾股数:满足a2+b2=c2的三个正整数
选做题:P60习题18.2:第5、6题
必做题:P60习题18.2:第1、2 、3 、4题
初中数学沪科版八年级下册18.2 勾股定理的逆定理教学课件ppt: 这是一份初中数学沪科版八年级下册18.2 勾股定理的逆定理教学课件ppt,共25页。PPT课件主要包含了知识要点,勾股定理的逆定理,勾股数,直角三角形,钝角三角形,即A′B′c,特别说明,c2625,c2121,练一练等内容,欢迎下载使用。
初中数学沪科版八年级下册18.2 勾股定理的逆定理教学ppt课件: 这是一份初中数学沪科版八年级下册18.2 勾股定理的逆定理教学ppt课件,共23页。PPT课件主要包含了逐点学练,本节小结,作业提升,学习目标,本节要点,学习流程,感悟新知,知识点,勾股定理的逆定理,勾股数等内容,欢迎下载使用。
初中数学沪科版八年级下册18.2 勾股定理的逆定理优质课件ppt: 这是一份初中数学沪科版八年级下册18.2 勾股定理的逆定理优质课件ppt,文件包含第1课时勾股定理的逆定理ppt、第2课时勾股定理的逆定理的应用ppt、182勾股定理的逆定理doc等3份课件配套教学资源,其中PPT共36页, 欢迎下载使用。













