八年级下册19.2 平行四边形评优课ppt课件

这是一份八年级下册19.2 平行四边形评优课ppt课件，文件包含1923平行四边形的判定ppt、1923平行四边形的判定教学设计doc、1923平行四边形的判定同步练习doc等3份课件配套教学资源，其中PPT共29页， 欢迎下载使用。

平行四边形的定义：两组对边分别平行的四边形叫做平行四边形
定义是平行四边形的原始的判定方法
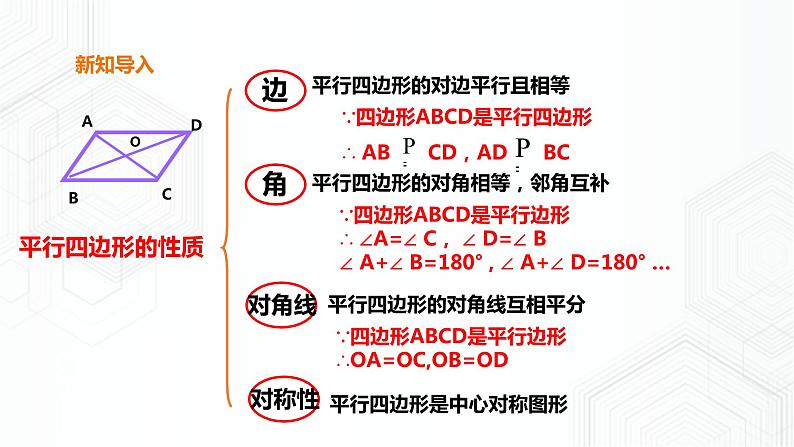
平行四边形的对边平行且相等
平行四边形的对角线互相平分
平行四边形的对角相等，邻角互补
∵四边形ABCD是平行边形 ∴OA=OC,OB=OD
平行四边形是中心对称图形
∵四边形ABCD是平行边形 ∴ ∠A=∠ C， ∠ D=∠ B∠ A+∠ B=180° , ∠ A+∠ D=180° …
平行四边形的两组对边分别相等；
我们得到的这些逆命题都成立？我们一起探讨一下吧
平行四边形的对角线互相平分；
思考：我们已经学习了平行四边形的性质，那么这些的逆命题各是什么呢？
一组对边平行且相等的四边形是平行四边形；
对角线互相平分的四边形是平行四边形.
两组对边分别相等的四边形是平行四边形；
平行四边形的任一组对边平行且相等；
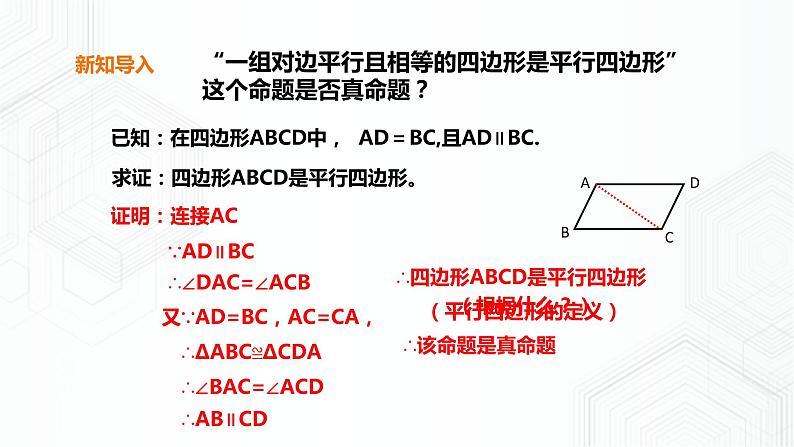
“一组对边平行且相等的四边形是平行四边形”这个命题是否真命题？
求证：四边形ABCD是平行四边形。
又∵AD=BC，AC=CA，
∴四边形ABCD是平行四边形
已知：在四边形ABCD中， AD＝BC,且AD∥BC.
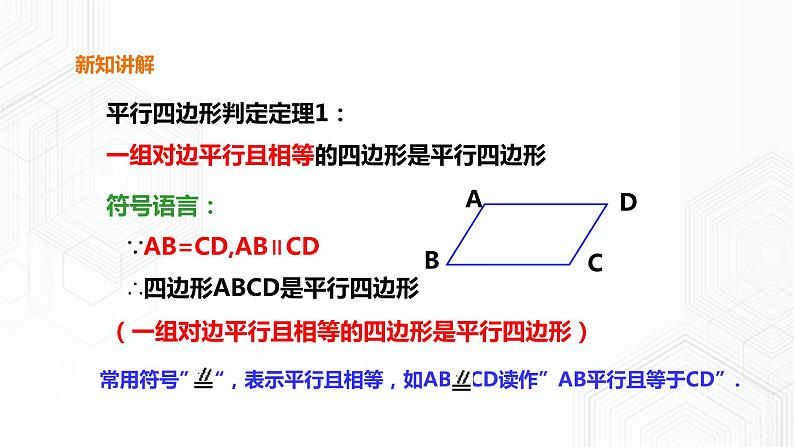
平行四边形判定定理1：一组对边平行且相等的四边形是平行四边形
∵AB=CD,AB∥CD
∴四边形ABCD是平行四边形
（一组对边平行且相等的四边形是平行四边形）
常用符号” “，表示平行且相等，如AB CD读作”AB平行且等于CD”.
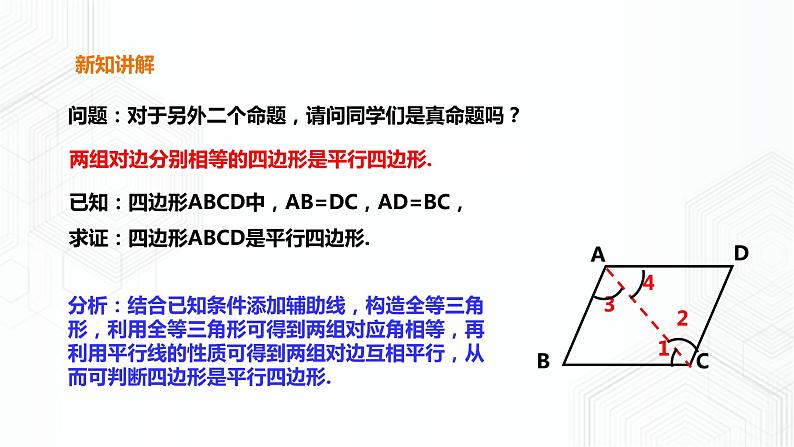
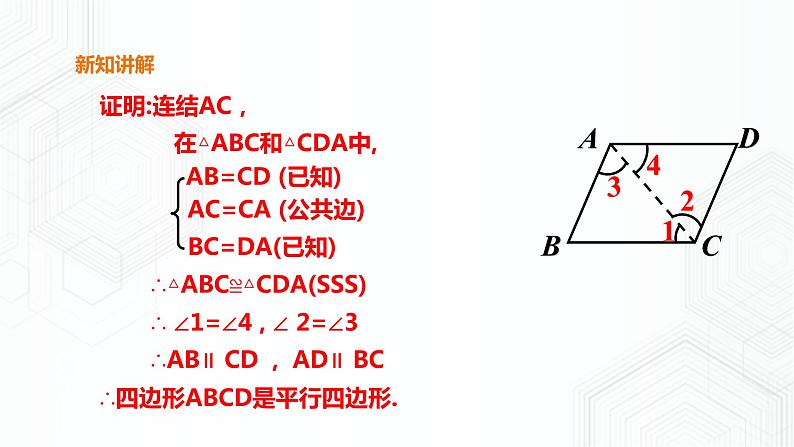
已知：四边形ABCD中，AB=DC，AD=BC，求证：四边形ABCD是平行四边形.
两组对边分别相等的四边形是平行四边形.
分析：结合已知条件添加辅助线，构造全等三角形，利用全等三角形可得到两组对应角相等，再利用平行线的性质可得到两组对边互相平行，从而可判断四边形是平行四边形.
问题：对于另外二个命题，请问同学们是真命题吗？
在△ABC和△CDA中,
AC=CA (公共边)
∴△ABC≌△CDA(SSS)
∴ ∠1=∠4 , ∠ 2=∠3
∴AB∥ CD , AD∥ BC
∴四边形ABCD是平行四边形.
已知：四边形ABCD中，OA=OC，OB=OD，求证：四边 形ABCD是平行四边形.
分析：根据已知条件构造全等三角形，利用全等三角形可得到两组对应角相等，再利用平行线的性质可得到两组对边互相平行，从而可判断四边形是平行四边形.
在△AOB和△COD中,
∠AOB=∠COD (对顶角相等)
∴△AOB≌△COD(SAS)
∴ ∠BAO=∠OCD , ∠ ABO=∠CDO
两组对边分别相等的四边形是平行四边形
平行四边形的判定定理2:
平行四边形的判定定理3：
对角线互相平分的四边形是平行四边形
OA=OC OB=OD
AB=DC AD=BC
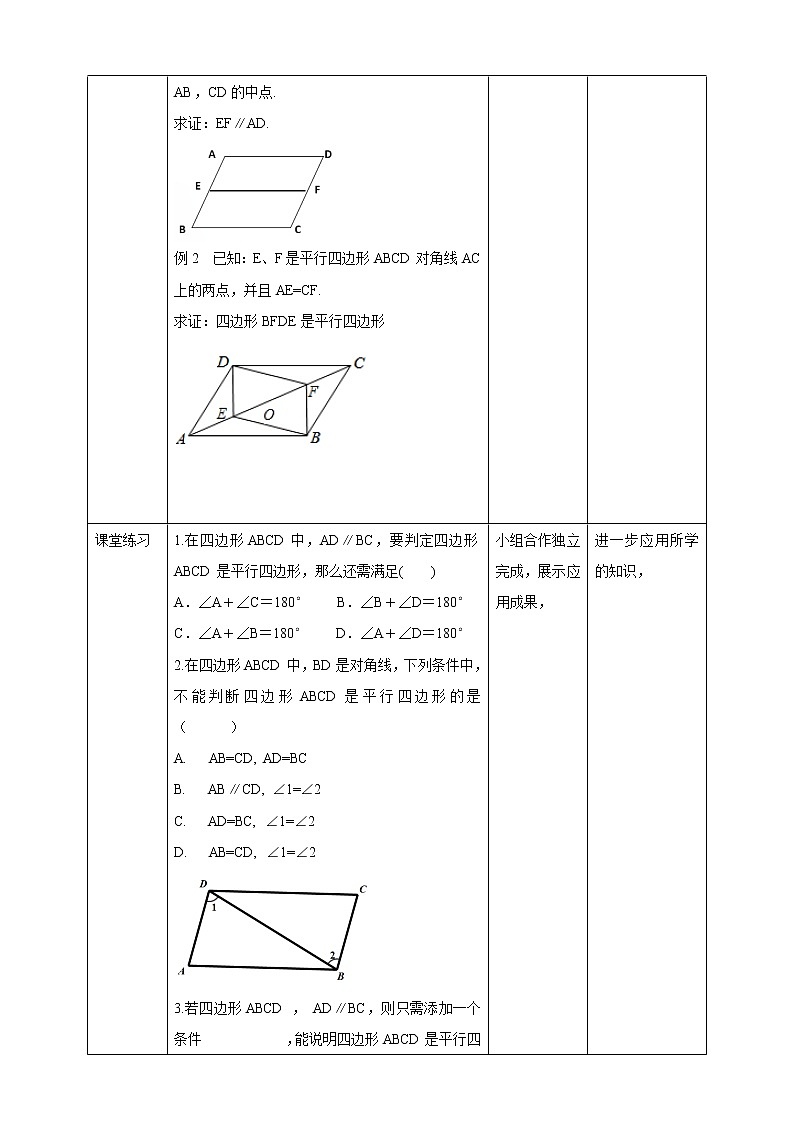
例1 　已知：如图，在□ABCD中，E、F分别是AB，CD的中点.求证：EF∥AD.
分析：由E、F分别是AB，CD的中点，可得AE=DF,接合平行四边形的判定定理1：一组对边平行且相等的四边形是平行四边形，最后由平行四边形的性质可证结果.
例2　已知：E、F是平行四边形ABCD对角线AC上的两点，并且AE=CF.求证：四边形BFDE是平行四边形
分析：方法1，由平行四边形的性质接合已知可证得△ AED ≌ △ CFB(SAS)进而得BF=DE，利用对角线互相平分来证明即可.
∴AD ∥ BC且AD =BC
在△AED和△CFB中
方法2 分析：连接BD，接合已知条件，由平行四边形的判定定理3：对角线互相平分的四边形是平行四边形，可证结果.
1.在四边形ABCD中，AD∥BC，要判定四边形ABCD是平行四边形，那么还需满足(　　)A．∠A＋∠C＝180° B．∠B＋∠D＝180°C．∠A＋∠B＝180° D．∠A＋∠D＝180°
2.在四边形ABCD中，BD是对角线，下列条件中，不能判断四边形ABCD是平行四边形的是（ ）
A. AB=CD, AD=BCB. AB∥CD, ∠1=∠2C. AD=BC, ∠1=∠2D. AB=CD, ∠1=∠2
3.若四边形ABCD ， AD∥BC，则只需添加一个条件_ __ __，能说明四边形ABCD是平行四边形.
AD=BC或AB//CD
4. 如图所示，△ABC是等边三角形，P是其内任意一点，PD//AB,PE//BC,PF//AC,若△ABC的周长为24，则PD+PE+PF= .
5.能判定四边形ABCD是平行四边形的条件：∠A:∠B:∠C:∠D的值为（　　）
A. 1:2:3:4
B. 1:4:2:3
C. 1:2:2:1
D. 3:2:3:2
1.(2018玉林)在四边形ABCD中：①AB∥CD②AD∥BC③AB=CD④AD=BC，从以上选择两个条件使四边形ABCD为平行四边形的选法共有（　　）A．3种B．4种C．5种D．6种
【分析】根据平行四边形的判定方法中，①②、③④、①③、③④均可判定是平行四边形．
解：根据平行四边形的判定，符合条件的有4种，分别是：①②、③④、①③、③④．故选：B．
1.(2018玉林)在四边形ABCD中：①AB∥CD②AD∥BC③AB=CD④AD=BC，从以上选择两个条件使四边形ABCD为平行四边形的选法共有（　　）A．3种 B．4种 C．5种 D．6种
2.(2018东营)如图，在四边形ABCD中，E是BC边的中点，连接DE并延长，交AB的延长线于点F，AB=BF．添加一个条件使四边形ABCD是平行四边形，你认为下面四个条件中可选择的是（ ）AD=BC B. CD=BF C. ∠A=∠C D. ∠F=∠CDF
【分析】根据已知条件和平行四边形的判定,要证明四边形ABCD是平行四边形，只需AB ∥ CD ，而要证AB ∥ CD ，平行线的判定方法，可从4个选项中选出正确的选项.
解：正确答案是D,理由如下，
∵∠F=∠CDF, ∠CED=∠BEF,EC=BF
∴ △CDE ≌△BFE(AAS),CD ∥ AF
通过这节课的学习，你有哪些收获？
定义法：两组对边分别平行的四边形是平行四边形定理1：一组对边平行且相等的四边形是平行四边形定理2：两组对边分别相等的四边形是平行四边形定理3：对角线互相平分的四边形是平行四边形
对角线互相平分的四边形是平行四边形(判定定理3)
两组对边分别平行的四边形是平行四边形(定义法)
两组对边分别相等的四边形是平行四边形(判定定理1)
一组对边平行且相等的四边形是平行四边形(判定定理2)
两组对角分别相等的四边形是平行四边形(定义拓展)
1.必做：课本85页习题19.2第9,11题2.选做：自主探究平行四边形的其他判定方法.