沪科版八年级下册19.2 平行四边形优秀课件ppt

这是一份沪科版八年级下册19.2 平行四边形优秀课件ppt，文件包含1924三角形的中位线定理ppt、1924三角形的中位线定理教学设计doc、1924三角形的中位线定理同步练习doc等3份课件配套教学资源，其中PPT共34页， 欢迎下载使用。

对角线互相平分的四边形是平行四边形(判定定理3)
两组对边分别平行的四边形是平行四边形(定义法)
两组对边分别相等的四边形是平行四边形(判定定理1)
一组对边平行且相等的四边形是平行四边形(判定定理2)
两组对角分别相等的四边形是平行四边形(定义拓展)
(1)在横格纸上画直线l1，使得l1与横线垂直，观察l1被个条子横线分成的线段是否相等？(2)再画一条直线l1那么 l2被各条横线分成的线段有何关系？
如果一组平行线在一条直线上截得的线段相等，那么在其他直线上截得的线段也相等.如何来证明？
已知直线l1 、 l2 、 l3互相平行，直线AC与直线A1C1分别交直线l1 、 l2 、 l3于点A ， B ， C，和点A1 ， B1 ， C1，且AB=BC，求证A1B1=B1C1
证明:过点B1作EF平行AC ，分别交直线L1 、 L2于点EF,∴四边形ABB1E，BCFB1都是平行四边形
结论：如果一组平行线在一条直线截得的线段相等，那么在其他直线上接的线段也相等．
符号语言∵直线l1 ∥ l2 ∥ l3 ， AB=BC， ∴ A1B1=B1C1
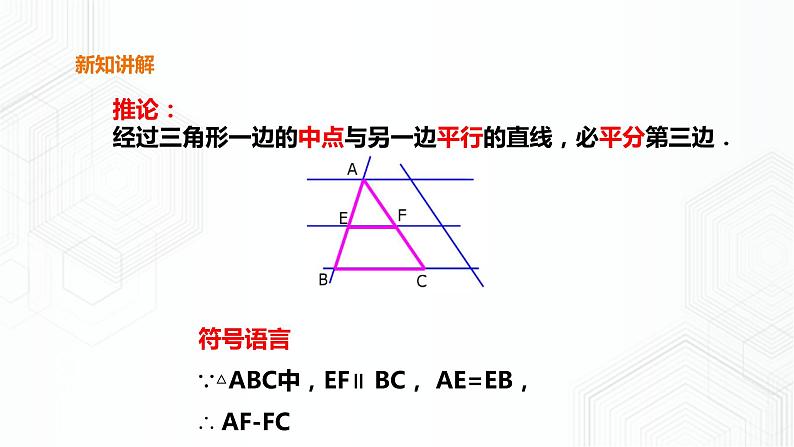
推论：经过三角形一边的中点与另一边平行的直线，必平分第三边．
符号语言∵△ABC中，EF∥ BC， AE=EB， ∴ AF-FC
定义：像EF这样，连接三角形两边中点的线段叫做三角形的中位线．
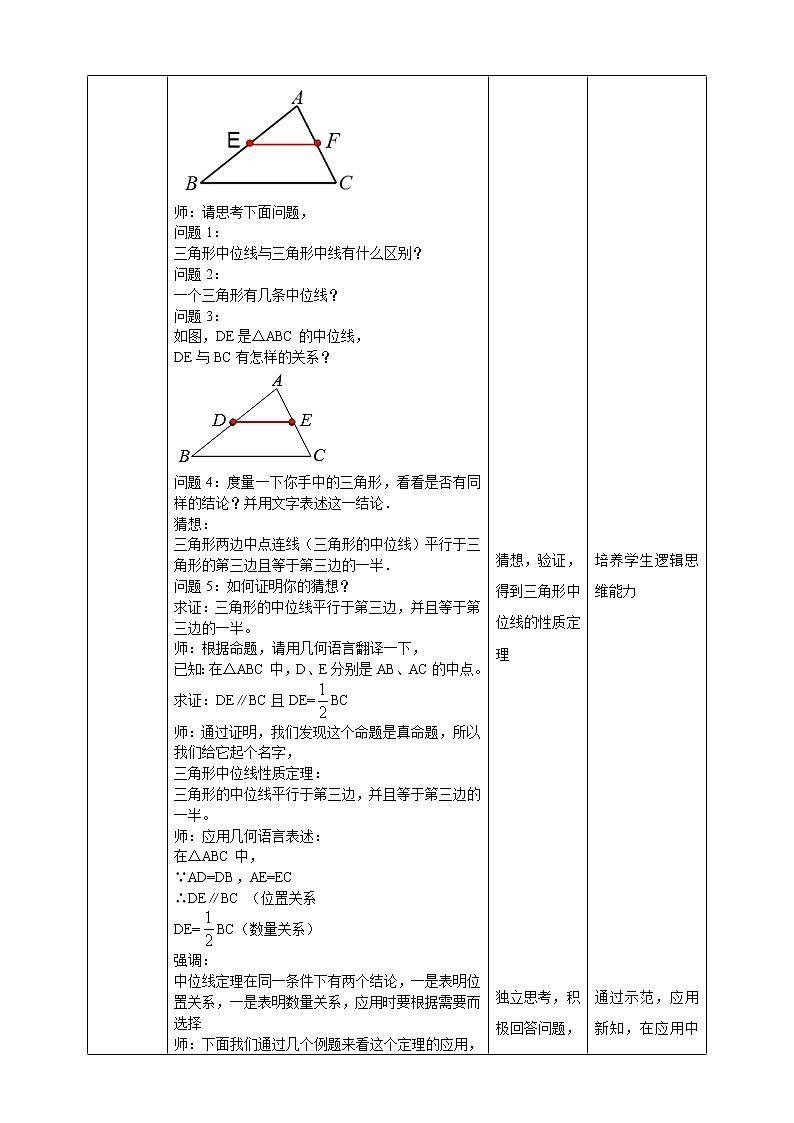
问题1：一个三角形有几条中位线？
所以前的推论也被称为三角形的中位线的判定：经过三角形一边的中点与另一边平行的直线，必平分第三边．
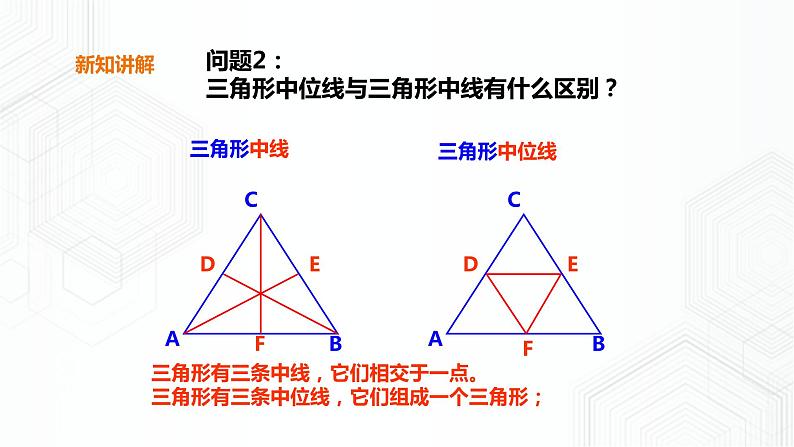
三角形有三条中线，它们相交于一点。三角形有三条中位线，它们组成一个三角形；
问题2：三角形中位线与三角形中线有什么区别？
问题3：如图，DE是△ABC的中位线，DE与BC有怎样的关系？
度量一下你手中的三角形，看看是否有同样的结论？并用文字表述这一结论．
猜想：三角形两边中点连线（三角形的中位线）平行于三角形的第三边且等于第三边的一半．
问题5：如何证明你的猜想？
已知：点D、E分别为△ABC的边AB、AC的中点.
先过点D作DE′∥BC， DE′交AC于点E′ ，由三角形中位线的判定，可知点E′与点E重合，
再过点D作DF∥AC， DF交BC于点F，由三角形中位线的判定，可知BF=CF ，最后由四边形DFCE是平行四边形， 进而可得结论，
过点D作DE′∥BC， DE′交AC于点E′ ，由三角形中位线的判定，可知点E′与点E重合，∴ DE∥BC
同理，过点D作DF∥AC， DF交BC于点F，由三角形中位线的判定，则点F为BC的中点，∴四边形DFCEO为平行四边形
三角形中位线性质定理：
三角形的中位线平行于第三边，并且等于第三边的一半。
在△ABC中，∵AD=DB，AE=EC ∴DE∥BC （位置关系）
强调：中位线定理在同一条件下有两个结论，一是表明位置关系，一是表明数量关系，应用时要根据需要而选择。
由_____得△ADE≌△CFE
四边形BCFD是平行四边形。
延长DE到F，EF=DE，连接FC
延长DE到F，使EF=DE．
∴四边形BCFD是平行四边形．
∴△ADE≌△CFE．
∴∠ADE=∠F,AD=CF,
∵AE=CE，∠AED=∠CEF， DE=EF ，
在△ADE与△CFE中．
1.图中有几个全等三角形，你是怎么知道的？你能证明吗？
2.图中有几个平行四边形？你能证明吗？
①中位线DE、EF、DF把△ABC分成四个全等的三角形；有三个共边的平行四边形，它们是四边形ADFE和BDEF和DFCE.
②顶点是中点的三角形，我们称之为中点三角形；
中点三角形的周长是原三角形的周长的一半.
中点三角形的面积是原三角形的面积的四分之一
例1　已知，如图，在△ABC中，AD=DB，BF =FC，AE=EC求证：AF、DE互相平分.
分析：连接DF 、EF，有已知条件，根据中位线的性质可得四边形ADFE是平行四边形，再由平行四边形的性质可得结果.
证明：连接DF、EF
∵AD=DB，BF=FC
∴四边形ADFE是平行四边形
∴AF、DE互相平分
三角形一条边中位线与第三边上的中线互相平分，
例2 已知:如图,在四边形ABCD中, E,F,G,H分别为各边的中点.求证:四边形EFGH是平行四边形.
分析:将四边形ABCD分割为三角形,利用三角形的中位线可转化两组对边分别平行或一组对边平行且相等来证明.
∵E,F,G,H分别为各边的中点,
∴ EF∥HG, EF=HG.
∴四边形EFGH是平行四边形.
应用三角形中位线定理的关键在于：
1.如图，在△ABC中，D、E分别为AB、AC的中点,DE=3cm, ∠C＝70°,那么BC= cm, ∠AED＝ °.
2.若在△ABC中， D、E、F分别是AB、AC、BC的中点, AB、AC、BC的长分别为6cm、8cm和10cm. 则△DEF的周长是 cm.
3.A,B两村相隔一座大山，你能想办法测出A,B两村的直线距离AB的大小吗？若MN=360 m，则AB=_______.
测出MN的长，就可知A、B两点的距离.
解析：在AB外选一点C，使C能直接到达A和B，
连结AC和BC，并分别找出AC和BC的中点M、N.
如果，M、N两点之间还有阻隔，你有什么解决办法？
两次利用中位线，分别取CM和CN的中点.
4.如图，在Rt△ABC 中，∠C=90°, D是斜边AB的中点，E是BC的中点.
（2）若AB=10,DE=4, 求△ABC 的面积.
（1）DE⊥BC吗？为什么？
解：∵DE∥BC，∠C=90°，∴DE⊥BC.
解：∵DE=4，∴AC=8.
∵AB=10，AC=8,∴BC=6.
1.(2018巴中)如图，在Rt△ABC中，∠ACB=90°，点D、点E分别是边AB、AC的中点，点F在AB上，且EF∥CD．若EF=2，则AB=　 　．
【分析】由于E是AC的中点,而且EF ∥ CD ，可知CD=2EF=4,再根据三角形ABC中D是AB的中点，AB=2CD，据此可得结果.
解：∵E是AC中点，且EF∥CD，∴EF是△ACD的中位线，则CD=2EF=4，在Rt△ABC中，∵D是AB中点，∴AB=2CD=8，故答案为：8．
2.(2018达州)如图，△ABC的周长为19，点D，E在边BC上，∠ABC的平分线垂直于AE，垂足为N，∠ACB的平分线垂直于AD，垂足为M，若BC=7，则MN的长度为（　　）
【分析】证明△BNA≌△BNE，得到BA=BE，即△BAE是等腰三角形，同理△CAD是等腰三角形，根据题意求出DE，根据三角形中位线定理计算即可．
解：∵BN平分∠ABC，BN⊥AE，∴∠NBA=∠NBE，∠BNA=∠BNE，在△BNA和△BNE中，
∴△BNA≌△BNE，∴BA=BE，∴△BAE是等腰三角形，同理△CAD是等腰三角形，∴点N是AE中点，点M是AD中点（三线合一），∴MN是△ADE的中位线，∵BE+CD=AB+AC=19﹣BC=19﹣7=12，∴DE=BE+CD﹣BC=5，
1，本节课你通过怎样的学习收获到了什么？
3，定理有几个结论，如何应用？
两个结论，一是表明位置关系，一是表明数量关系，应用时要根据需要而选择。
1.知识方面：三角形中位线概念； 三角形中位线定理．
2.思想方法方面：转化思想．
必做题：P85习题19.2第14、15题，
选做题：顺次连接任意四边形的各边中点，所得到的一个新的四边形，判断这个新四边形是否一定是平行四边形？并说明理由．