初中沪科版19.4 综合与实践 多边形的镶嵌完整版课件ppt

这是一份初中沪科版19.4 综合与实践 多边形的镶嵌完整版课件ppt，文件包含194综合与实践多边形的镶嵌ppt、194综合与实践多边形的镶嵌教学设计doc、194综合与实践多边形的镶嵌同步练习doc等3份课件配套教学资源，其中PPT共35页， 欢迎下载使用。
一点空隙也没有.这是怎么铺设的呢?
请问:拼接点处是否被瓷砖完全覆盖，有空隙吗？是否重叠？
通过观察上面的地面及墙面，你发现它们有哪些共同特点？
用形状相同或不同的平面封闭图形，覆盖平面区域，使图形间既无缝隙又不重叠地全部覆盖，这在几何里叫做平面镶嵌。平面镶嵌也叫密铺。
各种图形拼接后要求既无缝隙，又不重叠
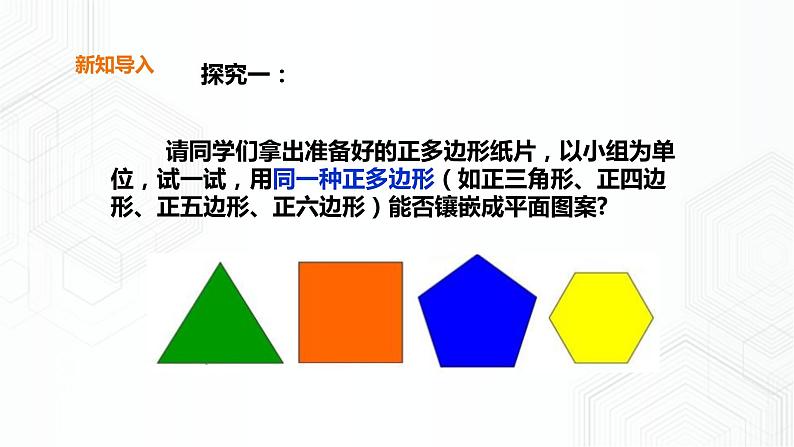
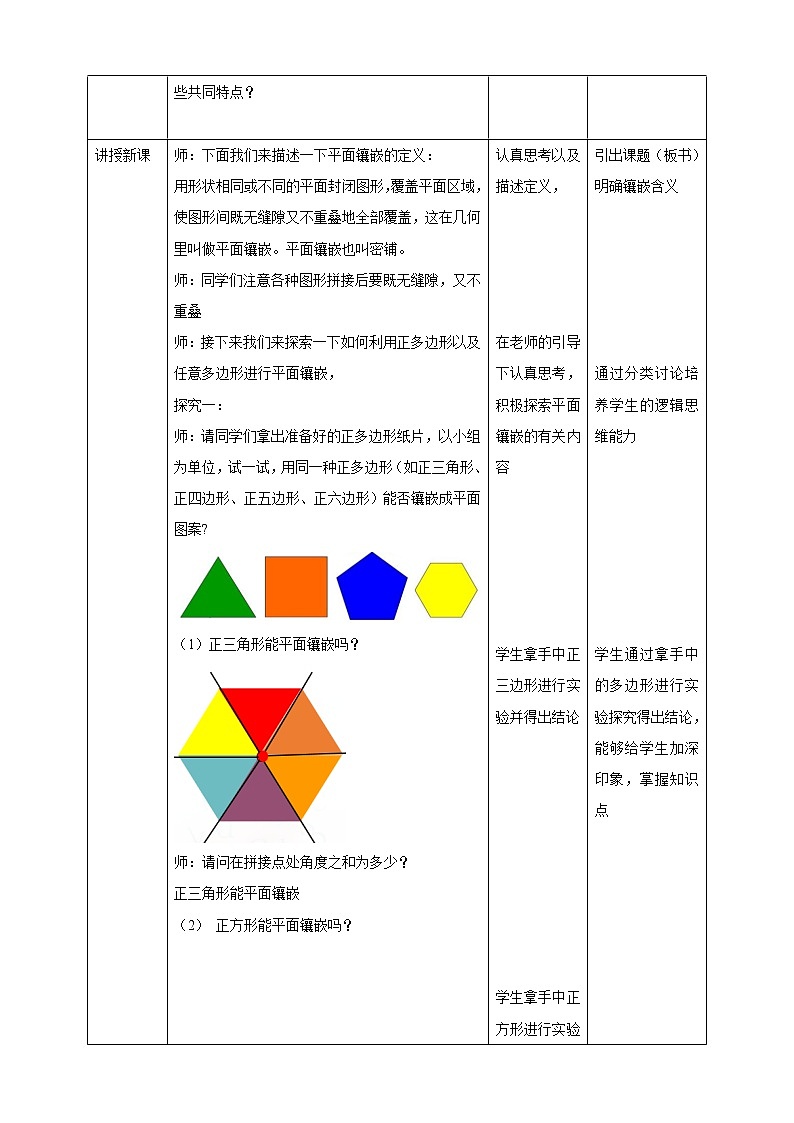
请同学们拿出准备好的正多边形纸片，以小组为单位，试一试，用同一种正多边形（如正三角形、正四边形、正五边形、正六边形）能否镶嵌成平面图案?
请问在拼接点处角度之和为多少？
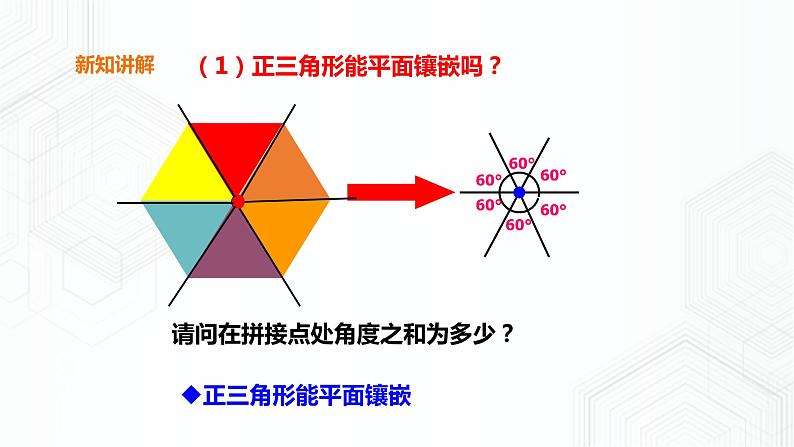
（1）正三角形能平面镶嵌吗？
（2） 正方形能平面镶嵌吗？
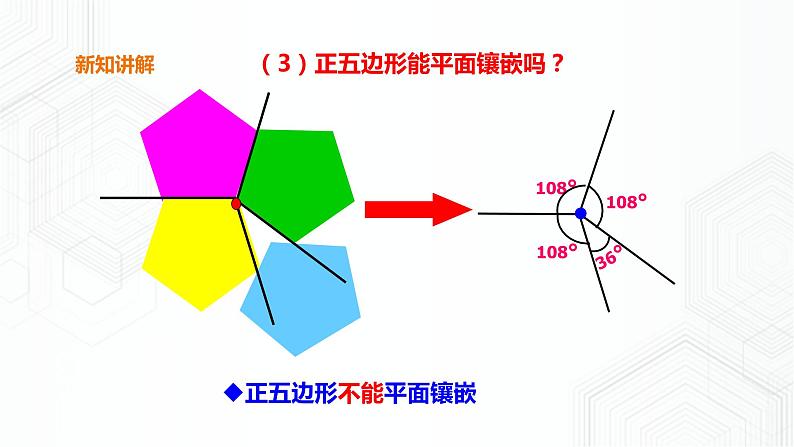
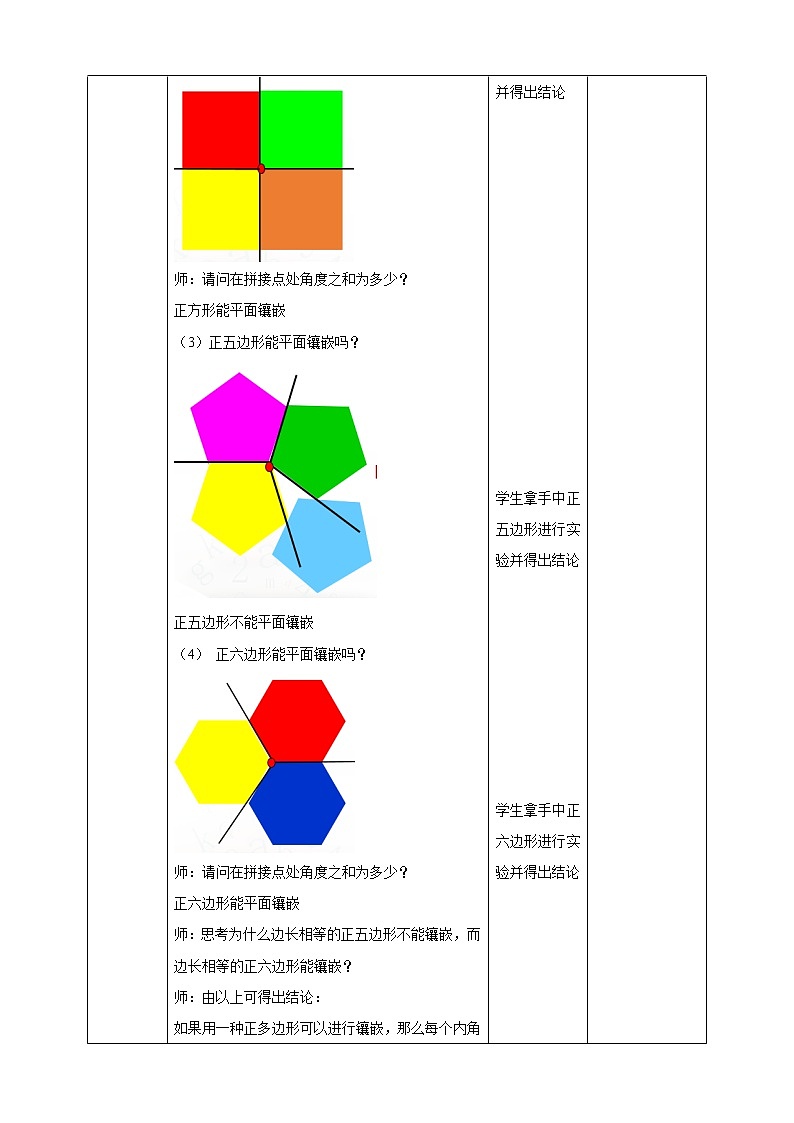
（3）正五边形能平面镶嵌吗？
（4） 正六边形能平面镶嵌吗？
6×60°= 360°
4×90°= 360°
4×108°＞ 360°
3×120°= 360°
3×108°＜ 360°
如果用一种正多边形可以进行镶嵌，那么每个内角都是360°的约数.
为什么边长相等的正五边形不能镶嵌，而边长相等的正六边形能镶嵌？
所以说：在正多边形里只有正三角形、正四边形、正六边形可以镶嵌，而其他的正多边形不能镶嵌．
小明搬新家了,他的房间要自己设计,地板想用两种正多边形来镶嵌，帮忙设计一个方案吧？
用边长相等的正三角形和正方形，能否镶嵌成平面图案？请你试一试！
解：设在一个拼接点周围有 m 个正三角形的角,n 个正方边形的角，
你知道正三角形及正方形各需要多少吗？
则有m·60° +n·90° =360°2m+3n=12∵ m,n 为正整数∴解为m=3.n=2
需要三个正三角形及两个正方形镶嵌。
请问：同一个组合会有不同的镶嵌效果吗？
你能找到它们的拼接点吗？
用边长相等的正三角形和正六边形进行平面镶嵌，你能拼出几种不同的图案？
你知道正三角形及正六边形各需要多少吗？
则有m·60° +n·120° =360°m+2n=6∵ m,n 为正整数∴解为m=2.n=2或者m=4.n=1
需要两个正三角形及两个正六边形镶嵌；或需要四个正三角形及一个正六边形镶嵌。
课外思考：还有没有其他的两种多边形组合镶嵌的形式呢？
结论：用两种正多边形镶嵌成平面图案的条件：1、拼接在同一个顶点处的所有角之和等于360°.2、两种正多边形边长相等.
五边形和菱形组合可以进行平面镶嵌
思考2：正五边形怎样才能进行平面镶嵌呢？
用几个形状、大小相同的任意三角形能镶嵌成一个平面图案吗？任意四边形呢？如果能镶嵌，请说明理由.
∵ ∠1+∠2+∠3=180°∴2(∠1+∠2+∠3)=360°∴任意三角形能镶嵌成平面图案。
∵∠1+∠2+∠3+∠4=360°
∴任意四边形能镶嵌成平面图案。
多边形镶嵌成平面图案的条件： 拼接在同一个顶点处的所有角之和等于360°.
1．只用下列图形不能镶嵌的是（ ）A．三角形 B．四边形 C．正五边形 D．正六边形
【分析】任意三角形的内角和是 180°，放在同一顶点处 6 个即能组成镶嵌．同理四边形的内角和是 360°，也能组成镶嵌．正六边形的每个内角是 120°，正五边形每个内角是 180°﹣360°÷5=108°，其中 180°，360°，120°能整除 360°，所以不适用的是正五边形．
解： A、任意三角形的内角和是 180°，放在同一顶点处 6 个即能密铺；B、任意四边形的内角和是 360°，放在同一顶点处 4 个即能密铺；C、正五边形的每一个内角是 180°﹣360°÷5=108°，不能整除 360°，所以不能密铺；D、正六边形每个内角是 120 度，能整除 360°，可以密铺．故选 C．
2.某商店出售下列四种形状的地砖：①正三角形；②正方形；③正五边形；④正六边形．若只选购其中一种地砖镶嵌地面，可供选择的地砖共有（ ）A．4 种 B．3 种 C．2 种 D．1 种
【分析】由镶嵌的条件知，判断一种图形是否能够镶嵌，只要看一看正多边形的内角度数是否能整除 360°，能整除的可以平面镶嵌，反之则不能．
解：①正三角形的每个内角是 60°，能整除 360°， 6 个能组成镶嵌②正方形的每个内角是 90°， 4 个能组成镶嵌；③正五边形每个内角是 180°﹣360°÷5=108°，不能整除 360°，不能镶嵌；④正六边形的每个内角是 120°，能整除 360°， 3 个能组成镶嵌；故若只选购其中某一种地砖镶嵌地面，可供选择的地砖共有 3 种．故选 B．
3.一幅图案在某个顶点处由三个边长相等的正多边形镶嵌而成．其中的两个分别是正方形和正六边形，则第三个正多边形的边数是 　　　．
【分析】正多边形的组合能否进行平面镶嵌， 关键是看位于同一顶点处的几个角之和能否为 360°．若能，则说明可以进行平面镶嵌；反之，则说明不能进行平面镶嵌．
解：∵正方形的一个内角度数为 180°﹣360°÷4=90°， 正六边形的一个内角度数为 180°﹣360°÷6=120°，∴需要的多边形的一个内角度数为 360°﹣90°﹣120°=150°，∴需要的多边形的一个外角度数为 180°﹣150°=30°，∴第三个正多边形的边数为 360÷30=12．故答案为： 12．
（2016•四川遂宁）下列图形中，单独选用一种图形不能进行平面镶嵌的是（  ） A．正三角形  B．正四边形  C．正六边形   D． 正八边形 
分析：几何图形镶嵌成平面的关键是围绕一点拼在一起的多边形的内角加在一起恰好组成一个周角．360°为正多边形一个内角的整数倍才能单独镶嵌．
解：A、正三边形的一个内角度数为180﹣360÷3=60°，是360°的约数，能镶嵌平面，不符合题意B、正四边形的一个内角度数为180﹣360÷4=90°，是360°的约数，能镶嵌平面，不符合题意；C、正方形的一个内角度数为180﹣360÷6=120°，是360°的约数，能镶嵌平面，不符合题意；D、正八边形的一个内角度数为180﹣360÷8=135°，不是360°的约数，不能镶嵌平面，符合题意． 故选：D
（1）只用一种正多边形；（2）同时用两种正多边形；（3）用一种非正多边形。
可以用同一种正多边形镶嵌的图形只有正三角形，正四边形，正六边形.
3. 用一种形状、大小完全相同的一般三角形、四边形也能进行平面镶嵌。
2. 两种或两种以上的正多边形组合在一起可以进行平面镶嵌
下面给出两个课题（每位同学从两个中任选一个）1.收集生活中的各种镶嵌地板、地砖、墙壁、墙纸的图案，把他们复制下来与同学交流，并研究他们的构成和拼接方法。2.请你用课上所学知识，设计一幅镶嵌艺术画.