


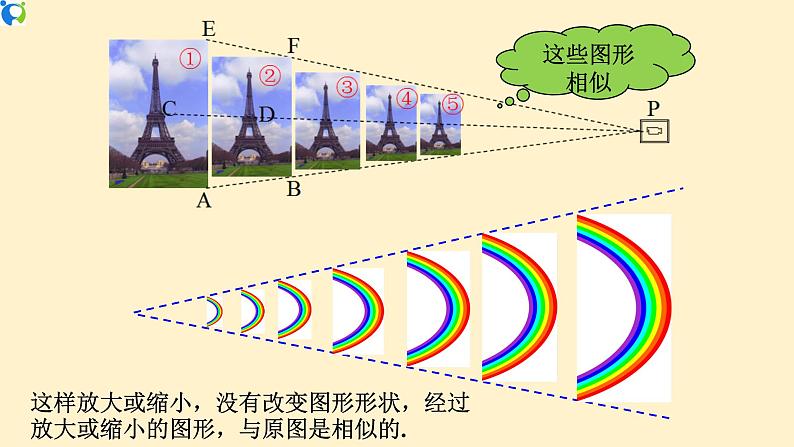
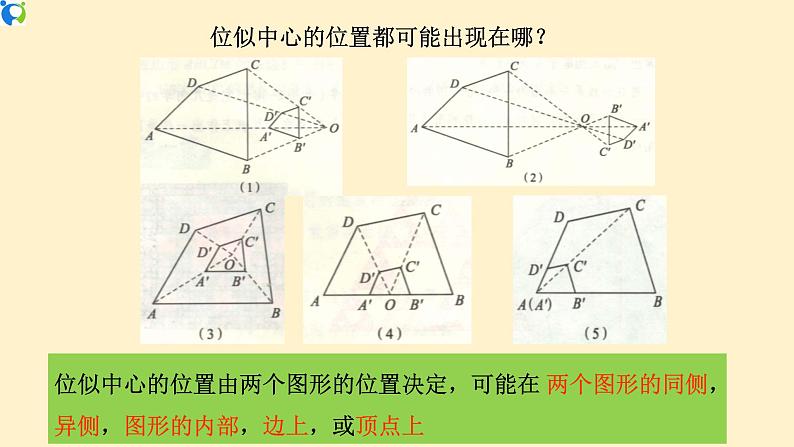


人教版九年级下册第二十七章 相似27.3 位似完整版ppt课件
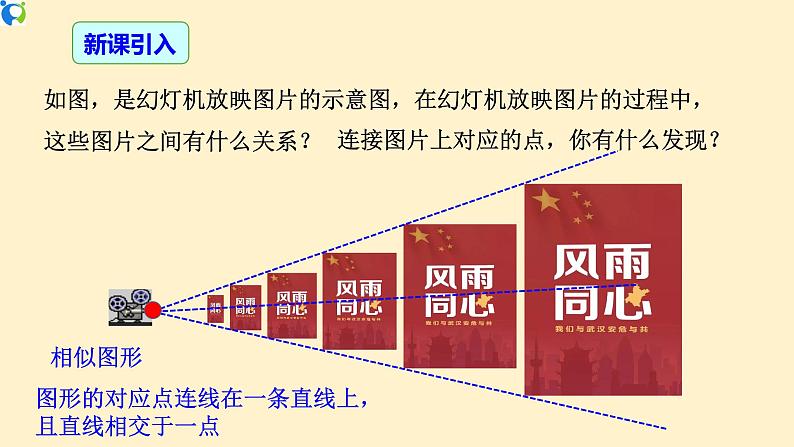
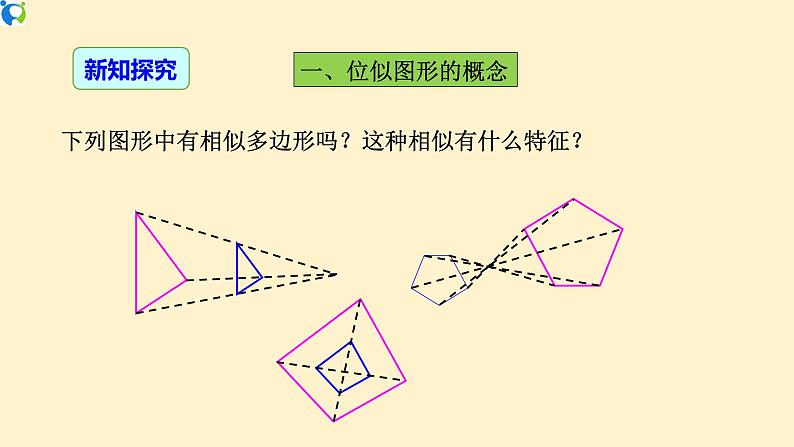
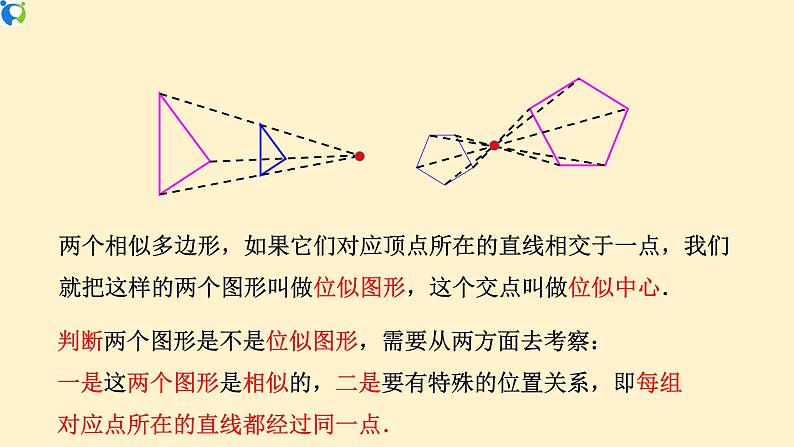
展开27.3 位似(第1课时)位似图形的概念、性质及画法
同步练习
一、单选题
类型一、位似图形的识别
1.如图是与位似的三角形的几种画法,其中正确的有( )
A.1个 B.2个 C.3个 D.4个
2. 如图,在△ABC所在平面上任意取一点O(与A、B、C不重合),连接OA、OB、OC,分别取OA、OB、OC的中点A1、B1、C1,再连接A1B1、A1C1、B1C1得到△A1B1C1,则下列说法不正确的是( )
A.△ABC与△A1B1C1是位似图形 B.△ABC与是△A1B1C1相似图形
C.△ABC与△A1B1C1的周长比为2:1 D.△ABC与△A1B1C1的面积比为2:1
3.如图,已知ABC,任取一点O,连AO,BO,CO,分别取点D,E,F,使OD=AO,OE=BO,OF=CO,得DEF.下列说法中,错误的是( )
A.DEF与ABC是位似三角形 B.OAC与ODF是位似三角形
C.DEF与ABC周长的比是1:3 D.图中位似的两个三角形面积比是1:9
类型二、判断位似中心
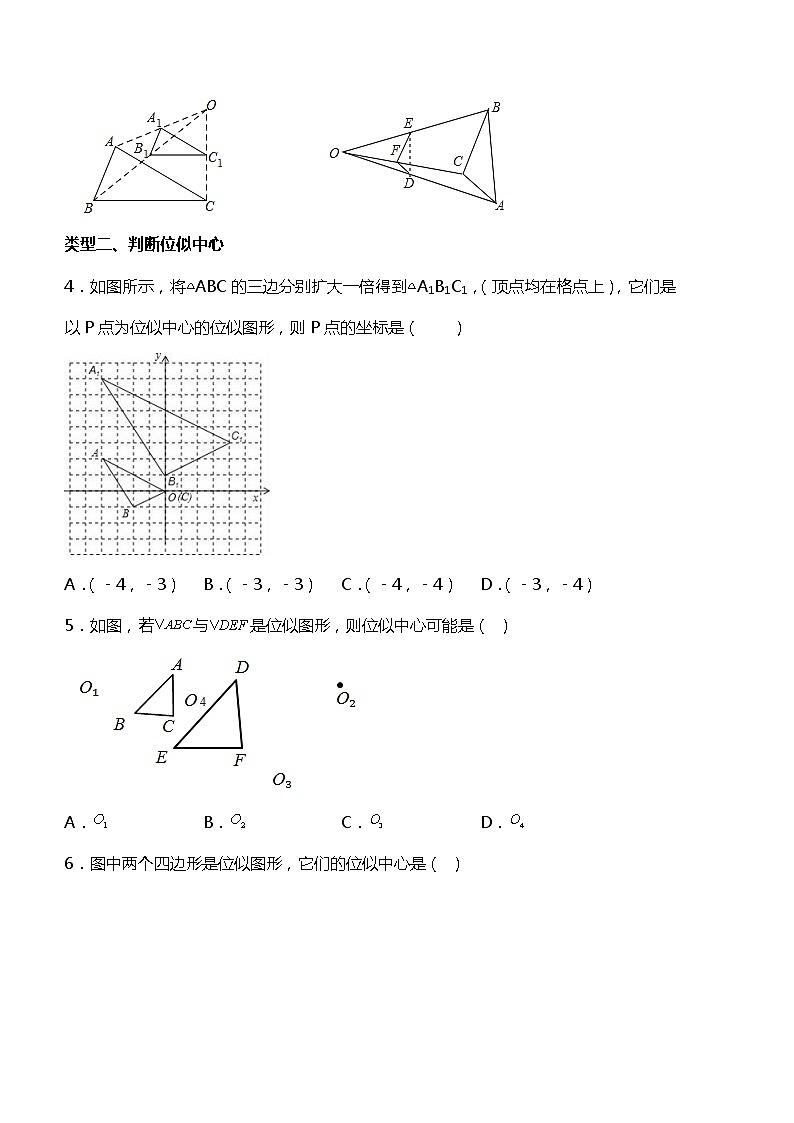
4.如图所示,将△ABC的三边分别扩大一倍得到△A1B1C1,(顶点均在格点上),它们是以P点为位似中心的位似图形,则P点的坐标是( )
A.(﹣4,﹣3) B.(﹣3,﹣3) C.(﹣4,﹣4) D.(﹣3,﹣4)
5.如图,若与是位似图形,则位似中心可能是( )
A. B. C. D.
6.图中两个四边形是位似图形,它们的位似中心是( )
A.点M B.点N C.点O D.点P
类型三、位似图形的相关概念
7.如图,四边形ABCD与四边形EFGH位似,其位似中心为点O,且,则=( )
A. B. C. D.
8.如图,以点O为位似中心,把放大为原图形的2倍得到,以下说法错误的是( )
A.点A,O,三点在同一条直线上 B.
C. D.
9.下列说法正确的是( )
A.若点C是线段AB的黄金分割点,AB=2,则AC=
B.平面内,经过矩形对角线交点的直线,一定能平分它的面积
C.两个正六边形一定位似 D.菱形的两条对角线互相垂直且相等
类型四、位似图形的相似比
10.如图,△ABC与△DEF位似,点O为位似中心.已知OA∶OD=1∶2,则△ABC与△DEF的面积比为( )
A.1∶2 B.1∶3 C.1∶4 D.1∶5
11.△DEF和△ABC是位似图形,点O是位似中心,点D,E,F分别是OA,OB,OC的中点,若△DEF的面积是2,则△ABC的面积是( )
A.2 B.4 C.6 D.8
12.如图,五边形ABCDE和五边形A1B1C1D1E1是位似图形,且PA1=PA,则AB∶A1B1=( )
A. B. C. D.
二.填空题
类型一、位似图形的识别
13.已知,如图2,A′B′∥AB,B′C′∥BC,且OA′∶A′A=4∶3,则△ABC与________是位似图形,位似比为________;△OAB与________是位似图形,位似比为________.
14.如图,以点O为位似中心,将放大得到若,则与的面积之比为___________.
15.如图,E、P、F分别是AB、AC、AD的中点,则四边形AEPF与四边形ABCD________ (填“是”或“不是”)位似图形.
类型二、判断位似中心
16.已知是轴的正半轴上的点,是由等腰直角三角形以为位似中心变换得到的,如图,已知,,则位似中心点的坐标是________.
17.如图,△EFH和△MNK是位似图形,其位似中心是点________.
18.如图,正方形OEFG和正方形ABCD是位似图形,点F的坐标为(1,1),点C的坐标为(4,2),则这两个正方形位似中心的坐标是______
类型三、位似图形的相关概念
19.顶点的坐标分别为,以坐标原点O为位似中心,画出放大的,使得它与的位似比等于2∶1,则点C的对应点坐标为________.
20.四边形与四边形位似,为位似中心,若,那么________.
21.在平面直角坐标系中,已知点A(-4,2),B(-2,-2),以原点为位似中心,位似比为,把△AOB缩小,则点A的对应点A′的坐标是___________.
类型四、位似图形的相似比
22.如图,四边形与四边形位似,其位似中心为点,且,则____.
23.如图,四边形ABCD与四边形EFGH位似,位似中心点是点O,,则=_____.
24.如图,在平面直角坐标系中,已知△ABC与△DEF位似,原点O是位似中心,位似比,若AB=1.5,则DE=_____.
二、解答题
类型一、位似图形的识别
25.如图, 相交于点,连结.
(1)求证: ;
(2)直接回答与是不是位似图形?
(3)若,求的长.
类型二、判断位似中心
26.如图,△ABC与△A´B´C´是位似图形,且相似比为.
(1)在图中画出位似中心;
(2)若,求的长.
类型三、位似图形的相关概念
27.如图,已知△DEO与△ABO是位似图形,△OEF与△OBC是位似图形,试说明:OD·OC=OF·OA.
类型四、位似图形的相似比
28.如图,点,在的边上,点,在边上,射线在内,且点,在上,,..
试说明与是位似图形;
求与的位似比.
参考答案
1.D
【分析】
根据位似图形的性质判断即可.
【详解】
解:由位似图形的画法可得:4个图形都是的位似图形.
故选:D.
【点拨】本题主要考查了位似变换,正确把握位似图形的定义是解题关键.
2.D
【分析】
根据三角形中位线定理得到,根据位似变换的概念、相似三角形的性质判断即可.
【详解】
∵点A1、B1、C1分别是OA、OB、OC的中点,
∴,
∴△ABC与△A1B1C1是位似图形,A正确;
△ABC与是△A1B1C1相似图形,B正确;
△ABC与△A1B1C1的周长比为2:1,C正确;
△ABC与△A1B1C1的面积比为4:1,D错误;
故选D.
【点拨】本题考查的是位似变换,掌握位似变换的概念、相似三角形的性质是解题的关键.
3.D
【分析】
根据位似三角形的定义及性质即可判断.
【详解】
A、由题意知,△DEF与△ABC是位似三角形,故正确;
B、由题意知,△OAC与△ODF是位似三角形,故正确;
C、由于△DEF与△ABC是位似三角形,因而也是相似三角形,且相似比为1:3,从而周长的比也为1:3,故正确;
D、此选项没有指明是哪两个位似三角形,故错误.
故选:D.
【点拨】本题考查了位似三角形的定义及性质.熟练运用定义及性质是解题的关键.
4.A
【分析】
作直线AA1、BB1,这两条直线的交点即为位似中心.
【详解】
由图中可知,点P的坐标为(﹣4,﹣3).
故选A.
【点拨】用到的知识点为:两对对应点连线的交点为位似中心.
5.A
【分析】
根据位似中心的定义判断即可.
【详解】
如图所示,连接CF和BE并延长,相交于O1点,
∴可能的位似中心为O1点,
故选:A.
【点拨】本题考查位似图形的概念,掌握位似中心是对应点连线的交点是解题关键.
6.D
【分析】
根据位似变换的定义:对应点的连线交于一点,交点就是位似中心.即位似中心一定在对应点的连线上.
【详解】
点P在对应点M和点N所在直线上,再利用连接另两个对应点,得出相交于P点,即可得出P为两图形位似中心,
故选D.
【点拨】此题主要考查了位似图形的概念,根据位似图形的位似中心位于对应点连线所在的直线上得出是解题关键.
7.A
【分析】
根据位似图像的性质得到对应成比例即可求解.
【详解】
∵四边形ABCD与四边形EFGH位似,其位似中心为点O,
∴,
∵,
∴=
故选:A.
【点拨】此题主要考查位似图形的性质,解题的关键是熟知相似三角形对应成比例.
8.C
【分析】
根据位似的性质对各选项进行判断.
【详解】
解:∵点O为位似中心,把△ABC中放大到原来的2倍得到△A'B'C',
∴△ABC∽△A'B'C',AB∥A′B′
∴,点A,O,三点在同一条直线上.
∴,则C错误
故选:.
【点拨】本题考查了位似变换:如果两个图形不仅是相似图形,而且对应顶点的连线相交于一点,对应边互相平行,那么这样的两个图形叫做位似图形,这个点叫做位似中心.位似的性质:两个图形必须是相似形;对应点的连线都经过同一点;对应边平行(或共线).
9.B
【分析】
A.根据黄金分割点的定义,AC可能是较长线段,也可能是较短线段,分情况讨论即可;
B.矩形是中心对称图形,根据中心对称图形的性质,经过对称中心的任意一条直线都把它分成两个全等形,面积当然相等;
C.按照相似与位似关系判断即可;
D.利用菱形的性质判断即可.
【详解】
A. 解:根据题意得:
当AC是较长线段时,,
当AC是较短线段时,,,故此项错误;
B. 平面内,经过矩形对角线交点的直线,一定能平分它的面积,如图:
,故此项正确;
C.位似图形一定相似,相似图形不一定位似,两个正六边形一定相似,但不一定位似,故此项错误;
D. 菱形的两条对角线互相垂直,但不一定相等,对角线一定相等的是矩形,故此项错误.
故选B.
【点拨】此题考查了黄金分割、位似与相似的关系、矩形菱形的性质是解题的关键,特别注意A中应分类讨论,这里的AC可能是较长线段,也可能是较短线段.
10.C
【分析】
根据位似图形的性质即可得出答案.
【详解】
由位似变换的性质可知,
△ABC与△DEF的相似比为:1∶2
△ABC与△DEF的面积比为:1∶4
故选C.
【点拨】本题考查了位似图形的性质,熟练掌握性质定理是解题的关键.
11.D
【分析】
先根据三角形中位线的性质得到DE=AB,从而得到相似比,再利用位似的性质得到△DEF∽△ABC,然后根据相似三角形的面积比是相似比的平方求解即可.
【详解】
∵点D,E分别是OA,OB的中点,
∴DE=AB,
∵△DEF和△ABC是位似图形,点O是位似中心,
∴△DEF∽△ABC,
∴=,
∴△ABC的面积=2×4=8
故选D.
【点拨】本题考查了位似变换:如果两个图形不仅是相似图形,而且对应顶点的连线相交于一点,对应边互相平行,那么这样的两个图形叫做位似图形,这个点叫做位似中心.
12.B
【分析】
本题主要考查了位似变换的定义及作图,根据作图的方法可知AB:A1B1=PA:PA1,PA1= PA,从而求得AB:A1B1=3:2.
【详解】
解:∵PA1=PA,
∴PA:PA1=3:2,
又∵AB:A1B1=PA:PA1,
∴AB:A1B1=3:2.
故选B.
【点拨】本题主要考查了位似变换的作图,及性质相似比相等.
13.△A′B′C′ 7∶4 △OA′B′ 7∶4
【解析】
试题分析:位似图形的性质:对应边平行或在一条直线上,且成比例.A′B′∥AB,B′C′∥BC,且OA′∶A′A=4∶3,所以△ABC与△ 是位似图,位似比为 =
△OAB与△ 是位似图形,位似比是 =
14.
【分析】
根据位似图形的性质,运用相似比的平方等于面积比求解即可.
【详解】
由题,根据位似图形的性质可得:,
且放大得到,
∴△ABC∽△DEF,相似比为,
根据相似图形面积比等于相似比的平方,
∴,
故答案为:.
【点拨】本题考查位似图形的性质及相似三角形的面积比,熟记面积比等于相似比的平方是解题关键.
15.是
【解析】
由已知易得:AF:AD=AP:AC=AE:AB,
∴PF∥CD,PE∥BC,
∴△APF∽△ACD,△AEP∽△ABC,
∴四边形AEPF∽四边形ABCD,
∴根据位似图形的定义:“两个图形不仅相似,而且每组对应点的连线交于一点,对应边互相平行或在同一直线上,则这两个图形叫位似图形”可知:四边形AEPF和四边形ABCD是位似图形.
即答案为:“是”.
16.
【分析】
根据位似图形的概念,连接AG,与CE的交点即是点P.根据相似三角形的性质求得OP的长,即可得点P的坐标..
【详解】
如图,连接AG,
∵EO=1,DC=2,
∴△ACD与△GOE的位似比是2:1,
∴AD:OG=2:1,
∵△ADC是等腰直角三角形,
∴AD⊥x轴,
∴AD∥OG,
∴△OPG∽△DPA
∴PD:OP=2:1,
∵OD=2,
∴OP=,
∴位似中心P点的坐标是(,0).
故答案为(,0).
【点拨】本题考查了位似的相关知识,熟知位似是相似的特殊形式,位似比等于相似比是解决问题的关键.
17.B
【解析】
【分析】
根据位似中心的含义,得位似图形对应点连线的交点是位似中心.
【详解】
如图
∵△EFH和△MNK是位似图形,连接FN,HK交于点B,故点B是位似中心.
【点拨】本题考查了位似图形的相关知识,解题的关键是知道位似图形对应点连线的交点是位似中心.
18.(−2,0)或
【解析】
【分析】
根据已知可知需分当位似中心在两个正方形同旁和位似中心在两个正方形之间进行讨论;
【详解】
两个图形位似时,位似中心就是CF与x轴的交点,
设直线CF解析式为y=kx+b,将C(4,2),F(1,1)代入,得
,解得,即
令y=0得x=−2,
∴O′坐标是(−2,0).
当OC是对应点时,BG是对应点,则OC和NG的交点就是对称中心,
设OC的解析式是y=mx,则4m=3,
解得:,则OC的解析式是
设BG的解析式是y=nx+d,
则
解得:
则直线BG的解析式是
则
解得:
则交点是
故答案为:(−2,0)或
【点拨】考查位似变换,两个位似图形的主要特征是:每对位似对应点与位似中心共线,不经过位似中心的对应线段平行.则位似中心就是两对对应点的延长线的交点.
19.或
【分析】
根据位似变换的性质计算即可.
【详解】
解:如图所示:
以坐标原点O为位似中心,放大的△A1B1C1,它与△ABC的位似比等于2: 1,
点C的坐标为(3,-4)
∴点C的对应点C1坐标为(3×2,-4×2) 或(-3×2,4×2)
即(6,-8)或(-6,8),
故答案为: (6,-8)或(-6,8).
【点拨】本题考查的是位似变换的性质,在平面直角坐标系中,如果位似变换是以原点为位似中心,相似比为k,那么位似图形对应点的坐标的比等于k或-k.
20.
【分析】
四边形ABCD与四边形A'B'C'D'位似,四边形ABCD∽四边形A'B'C'D'位似,可知AD∥A′D′,△OAD∽△OA′D′,求出相似比从而求得4:9.
【详解】
解:∵四边形ABCD与四边形A'B'C'D'位似
∴四边形ABCD∽四边形A'B'C'D'位似
∴AD∥A′D′
∴△OAD∽△OA′D′
∴OA:O′A′=AD:A′D′=2:3
∴4:9.
【点拨】本题考查了位似的相关知识,位似是相似的特殊形式,位似比等于相似比,其对应的面积比等于相似比的平方.
21.(-2,1)或(2,-1)
【解析】
试题解析:∵点A(-4,2),B(-2,-2),以原点O为位似中心,相似比为,把△AOB缩小,
∴点A的对应点A′的坐标是:(-2,1)或(2,-1).
22.
【分析】
直接利用位似图形的性质结合位似比等于相似比得出答案.
【详解】
解:∵四边形ABCD与四边形EFGH位似,其位似中心为点O,且,
∴,
则=.
故答案为.
【点拨】此题主要考查了位似变换,正确掌握位似图形的性质是解题关键.
23.
【详解】
试题分析:∵四边形ABCD与四边形EFGH位似,位似中心点是点O,
∴==,
则===.
故答案为.
点睛:本题考查的是位似变换的性质,掌握位似图形与相似图形的关系、相似多边形的性质是解题的关键.
24.4.5
【解析】
【分析】
根据位似图形的性质得出AO,DO的长,进而得出, ,求出DE的长即可
【详解】
∵△ABC与△DEF位似,原点O是位似中心,
∴,
∵,
∴,
∴,
∴DE=3×1.5=4.5.
故答案为4.5.
【点拨】此题考查坐标与图形性质和位似变换,解题关键在于得出AO,DO的长
25.(1)详见解析;(2)不是;(3)
【分析】
(1)根据已知条件可知,根据对顶角相等可知,由此可证明;
(2)根据位似图形的定义(如果两个图形不仅是相似图形,而且对应顶点的连线相交于一点,对应边互相平行,那么这样的两个图形叫做位似图形,这个点叫做位似中心.)
(3)由△ADP∽△BCP,可得,而∠APB与∠DPC为对顶角,则可证△APB∽△DPC,从而得,再根据即可求得AP的长.
【详解】
(1)证明:∵,
∴;
(2)点A、D、P的对应点依次为点B、C、P,对应点的连线不相交于一点,故与不是位似图形;
(3)解:∵
∴
∵,
∴,
∴
∴.
【点拨】本题考查相似三角形的性质和判定,位似图形的定义.熟练掌握相似三角形的判定定理是解决此题的关键.
25.(1)见解析;(2)8
【分析】
(1)根据位似中心的性质,连接两组对应顶点,交点即为位似中心;
(2)根据和相似比即可求出.
【详解】
解:(1)如解图,连接,交于点,则点即为位似中心;
(2)∵与是位似图形,且相似比为,,
∴
【点拨】此题考查的是位似中心的确定和位似图形的性质,掌握位似中心即为对应顶点连线的交点和位似图形的性质是解决此题的关键.
27.见解析
【解析】
试题分析:
由题意易得:△ODE∽△OAB,△OEF∽△ABC,从而可得:OD:OA=OE:OB,OF:OC=OE:OB,由此即可得到:OD:OA=OF:OC,从而由比例的基本性质可得结论.
试题解析:
由题意可知:△ODE∽△OAB,△OEF∽△ABC,
∴OD:OA=OE:OB,OF:OC=OE:OB,
∴OD:OA=OF:OC,
∴OD·OC=OF·OA.
28.(1)详见解析;(2).
【解析】
【分析】
(1)利用平行线的性质以及平行线分线段成比例定理得出∠DFE=∠ACB,,即可得出△ACB∽△DFE,再利用两图形对应点交于点O,即可得出答案;
(2)利用位似图形的性质,得出相似比就是位似比.
【详解】
∵,,
∴,,,,
∴,,
∴,
∴与是位似图形;
∵与是位似图形,,
∴与的位似比为:.
【点拨】此题主要考查了位似变换,正确利用位似图形的定义得出是解题关键.
数学九年级下册27.3 位似备课课件ppt: 这是一份数学九年级下册<a href="/sx/tb_c28355_t3/?tag_id=26" target="_blank">27.3 位似备课课件ppt</a>,共28页。
数学九年级下册27.3 位似优质课课件ppt: 这是一份数学九年级下册27.3 位似优质课课件ppt,文件包含273位似第1课时位似图形的概念及画法pptx、273位似第1课时位似图形的概念及画法教案doc、273位似第1课时位似图形的概念及画法导学案doc等3份课件配套教学资源,其中PPT共28页, 欢迎下载使用。
九年级下册27.3 位似优秀课件ppt: 这是一份九年级下册27.3 位似优秀课件ppt,共20页。PPT课件主要包含了图片引入,★位似图形的概念,★位似图形的性质,★位似图形的画法等内容,欢迎下载使用。














