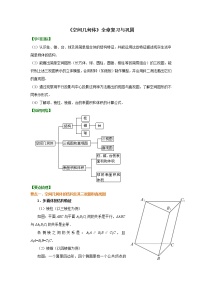
巩固练习_《空间几何体》全章复习与巩固（基础）

这是一份巩固练习_《空间几何体》全章复习与巩固（基础），共7页。
【巩固练习】1．下列结论中，正确的是（    ）    A．三角形绕其一边旋转一周后成一个圆锥    B．一个直角梯形绕其一边旋转一周后成为一个圆台    C．平行四边形绕其一边旋转一周后成为圆柱    D．圆面绕其一条直径旋转一周后成为一个球2．以下命题中真命题的序号是（    ）    ①若棱柱被一平面所截，则分成的两部分不一定是棱柱；    ②有两个面平行，其余各面都是梯形的几何体叫棱台；    ③用一个平面去截圆锥，底面和截面之间的部分组成的几何体叫圆台；    ④有两个面平行，其余各面都是平行四边形的几何体叫棱柱．A．③④    B．①④    C．①②④    D．①3．如图，某几何体的主视图与左视图都是边长为1的正方形，且体积为，则该几何体的俯视图可以是（    ）4．如图是某几何体的三视图，则该几何体的体积为（    ）        A．1    B．    C．    D．5．某几何体的三视图如图所示，则这个几何体的体积为（    ）        A．    B．    C．8    D．46．一个棱长为2的正方体的顶点都在球面上，则该球的表面积为（    ）A．4π    B．8π    C．12π    D．16π7．一个几何体的三视图如图所示，则这个几何体的体积是（    ）        A．    B．1    C．    D．28．某几何体的三视图如图所示，则该几何体的体积为（    ）        A．    B．    C．    D．9．某几何体的三视图如图所示，则该几何体的体积为（　　）           A．       B．          C．           D．10．一个棱长为2的正方体沿其棱的中点截去部分后所得几何体的视图如图所示，则该几何体的体积为（    ）        A．7    B．    C．    D．11．已知某几何体的三视图如图所示，其正视图为矩形，侧视图为等腰直角三角形，俯视图为直角梯形．则该几何体的表面积是________；体积是________．        12．已知A，B，C三点在球O的球面上，AB=BC=CA=3，且球心O到平面ABC的距离等于球半径的，则球O的表面积为________．13．正三棱柱ABC—A1B1C1内接于半径为2的球，若A，B两点的球面距离为π，则正三棱柱的体积为   　　．14．某几何体的三视图如图所示，作出该几何体直观图的简图，并求该几何体的体积．15．设如图是某几何体的三视图，求该几何体的体积和表面积．         【参考答案与解析】1．【答案】D【解析】在A中，直角三角形绕直角边旋转一周后成一个圆锥，绕斜边得到是两底部相等并重合的顶部方向相反的圆锥集合体，故A错误；    在B中，一个直角梯形绕其上底和下底中点连线旋转一周后成为一个圆台，故B错误；    在C中，矩形绕其一边旋转一周后成为圆柱，故C错误；    在D中，圆面绕其一条直径旋转一周后成为一个球，故D正确．    故选D．2．【答案】D【解析】①若棱柱被一平面所截，则分成的两部分不一定是棱柱；正确，当平面与棱柱的所有平面不平行时，截出的两个几何体不是棱柱．    ②有两个面平行，其余各面都是梯形的几何体叫棱台；不正确，不满足棱台的定义．    ③用一个平面去截圆锥，底面和截面之间的部分组成的几何体叫圆台；不正确；当平面与底面平行时，底面和截面之间的部分组成的几何体叫圆台．    ④有两个面平行，其余各面都是平行四边形的几何体叫棱柱，不正确，不满足棱柱的定义．故选：D．3．【答案】C.【解析】由该几何体的主视图和左视图可知该几何体是柱体，且其高为1，由其体积是可知该几何体的底面积是，由图知A的面积是1，B的面积是，C的面积是，D的面积是，故选C.4．【答案】B【解析】由三视图知几何体是一个四棱锥，四棱锥的底面是一个平行四边形，有两个等腰直角三角形，直角边长为1组成的平行四边形，四棱锥的一条侧棱与底面垂直，且侧棱长为1，∴四棱锥的体积是．故选B．5．【答案】A【解析】由已知中的三视图可得该几何体的直观图如下图所示：        该几何体是一个四棱锥A—CDEF和一个三棱锥组F—ABC成的组合体，四棱锥A—CDEF的底面面积为4，高为4，故体积为：，三棱锥组F—ABC的底面面积为2，高为2，故体积为：，故这个几何体的体积，故选：A6．【答案】C7．【答案】A【解析】由已知易得该几何体是一个以正视图为底面，以1为高的四棱锥由于正视图是一个上底为1，下底为2，高为1的直角梯形故棱锥的底面面积则故选A8．【答案】A【解析】该几何体为三棱柱与三棱锥的组合体，如右图，三棱柱的底面是等腰直角三角形，其面积，高为1；故其体积V1=1×1=1；三棱锥的底面是等腰直角三角形，其面积，高为1；故其体积；故该几何体的体积；故选A． 9．【答案】B【解析】由题意可知几何体的形状是放倒的圆柱，底面半径为1，高为2，左侧与一个底面半径为1，高为1的半圆锥组成的组合体，几何体的体积为：．故选B．10．【答案】D【解析】依题意可知该几何体的直观图如图所示，其体积为正方体的体积去掉两个三棱锥的体积．即：，    故选D． 11．【答案】．【解析】由已知中的三视图，可知该几何体是一个三棱柱切去一个三棱锥所得的组合体，其直观图如图所示：        平面ABFE的面积为32，平面BCDF的面积为：24，平面ABC的面积为：8，平面DEF的面积为：，平面ADE的面积为：，平面ACD的面积为：，故组合体的表面为：，棱柱ABC—EFG的体积为：64，棱锥D—BFG的体积为：，故组合体的体积为：，故答案为：．12．【答案】【解析】设球的半径为r，O＇是△ABC的外心，外接圆半径为，∵球心O到平面ABC的距离等于球半径的，∴得，得．球的表面积．故答案为：．13．【答案】8【解析】由条件可得，所以，O到平面ABC的距离为，所以所求体积等于8．14．【解析】根据几何体的三视图，得该几何体是底面为正方形，高为1的四棱锥，且底面正方形的边长为1；画出该四棱锥的直观图如图所示：∴该四棱锥的体积为V=15．【答案】42+9π【解析】由已知中的三视图，可得该几何体是一个长方体和一个球形成的组合体，长方体的体积为3×3×2=18，球的体积为：，故组合体的体积，长方体的表面积为2(2×3+2×3+3×3)=42，球的表面积为：，故组合体的表面积S=42+9π．