三角函数综合_知识讲解_基础练习题

三角函数综合

【学习目标】

1.理解任意角的概念、弧度的意义，能正确地进行弧度与角度的换算.

2.掌握任意角的正弦、余弦、正切的定义，掌握同角三角函数的基本关系式，掌握正弦、余弦的诱导公式，理解周期函数与最小正周期的意义.

3.能正确运用三角公式，进行简单三角函数式的化简、求值和恒等式证明.

4.会用“五点法”画正弦函数、余弦函数和函数的简图，理解的物理意义.

5．掌握正弦函数、余弦函数的周期性、奇偶性、单调性等性质并能灵活应用．

6．熟练掌握正弦函数、余弦函数、正切函数、余切函数图象的形状，理解图象平移变换、伸缩变换的意义，并会用这两种变换研究函数图象的变化.

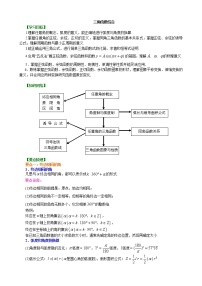
【知识网络】

【要点梳理】

要点一：终边相同的角

1．终边相同的角

凡是与终边相同的角，都可以表示成的形式.

要点诠释：

(1)终边相同的前提是：原点，始边均相同；

(2)终边相同的角不一定相等，但相等的角终边一定相同；

(3)终边相同的角有无数多个，它们相差的整数倍.

特例：

终边在x轴上的角集合，

终边在y轴上的角集合，

终边在坐标轴上的角的集合.

在已知三角函数值的大小求角的大小时，通常先确定角的终边位置，然后再确定大小.

2．弧度和角度的换算

(1)角度制与弧度制的互化：弧度，弧度，弧度

(2)弧长公式：(是圆心角的弧度数)，扇形面积公式：.

要点诠释：

(1)角有正负零角之分，它的弧度数也应该有正负零之分，如等等，一般地, 正角的弧度数是一个正数，负角的弧度数是一个负数，零角的弧度数是0,角的正负主要由角的旋转方向来决定.

(2)角的弧度数的绝对值是：，其中，是圆心角所对的弧长，是半径.

要点二：任意角的三角函数的定义、三角函数的符号规律、特殊角的三角函数值、同角三角函数的关系式、诱导公式：

1.三角函数定义：

角终边上任意一点为，设则：

要点诠释：

三角函数的值与点在终边上的位置无关，仅与角的大小有关.我们只需计算点到原点的距离,那么,,．

2.三角函数符号规律：

一全正，二正弦，三正切，四余弦(为正)；

要点诠释：

口诀的含义是在第一象限各三角函数值为正；在第二象限正弦值为正，在第三象限正切值为正，在第四象限余弦值为正．

3.特殊角的三角函数值

4.同角三角函数的基本关系：

要点诠释：

(1)这里“同角”有两层含义，一是“角相同”，二是对“任意”一个角(使得函数有意义的前提下)关系式都成立；

(2)是的简写；

(3)在应用平方关系时，常用到平方根，算术平方根和绝对值的概念，应注意“”的选取．

5.诱导公式(奇变偶不变，符号看象限):

sin()=sin，cos()=-cos，tan()=-tan

sin()=-sin，cos()=-cos，tan()=tan

sin()=-sin，cos()=cos，tan()=-tan

sin()=-sin，cos()=cos，tan()=-tan

sin()=sin，cos()=cos，tan()=tan，

sin()=cos，cos()=sin

sin()=cos，cos()=-sin

要点诠释：

(1)要化的角的形式为(为常整数)；

(2)记忆方法：“奇变偶不变，符号看象限”；

(3)必须对一些特殊角的三角函数值熟记，做到“见角知值，见值知角”；

(4)；.

要点三：正弦函数、余弦函数和正切函数的图象与性质

1.三角函数的图象与性质：

y=cosx的图象是由y=sinx的图象左移得到的.

2．三角函数的图象与性质：

要点四：函数的图象与性质

 1．“五点法”作简图

用“五点法”作的简图，主要是通过变量代换，设，由z取来求出相应的x，通过列表，计算得出五点坐标，描点后得出图象.

要点诠释：

用“五点法”作图的关键是点的选取，其中横坐标成等差数列，公差为.

2．的性质

(1)三角函数的值域问题

三角函数的值域问题，实质上大多是含有三角函数的复合函数的值域问题，常用方法有：化为代数函数的值域或化为关于的二次函数式，再利用换元、配方等方法转化为二次函数在限定区间上的值域.

(2)三角函数的单调性

函数的单调区间的确定，基本思想是把看作一个整体，比如：由解出的范围所得区间即为增区间，由解出的范围，所得区间即为减区间；

要点诠释：

（1）注意复合函数的解题思想；

（2）比较三角函数值的大小，往往是利用奇偶性或周期性在转化为属于同一单调区间上的两个同名函数值，再利用单调性比较.

3．确定的解析式的步骤

①首先确定振幅和周期，从而得到；

②确定值时，往往以寻找“五点法”中第一个零点作为突破口，要注意从图象的升降情况找准第一个零点的位置，同时要利用好最值点.

要点五：正弦型函数的图象变换方法

先平移后伸缩

的图象

的图象

的图象

的图象的图象.

先伸缩后平移

的图象

的图象

的图象

的图象的图象.

【典型例题】

类型一：三角函数的概念

例1．已知角的终边上一点，且，求的值.

【思路点拨】

【解析】由题设知，，所以，得，

从而，

解得或.

当时，， ；

当时，， ；

当时，， .

【总结升华】理解正弦函数和余弦函数的定义，三角函数值是比值，是一个实数，这个实数的大小和点在终边上的位置无关.

举一反三：

【变式1】已知角α的终边过点P(－8m，－6sin 30°)，且cos α＝－，则m的值为(　　)

A．－     B.      C．－     D.

【答案】B

【解析】r＝，

∴cos α＝，∴m>0，

∴，∴m＝±.∵m>0，∴m＝.

例2.已知角；

(1)在区间内找出所有与角有相同终边的角；

(2)集合，，那么两集合的关系是什么？

【答案】(1) 或(2)

【解析】(1)所有与角有相同终边的角可表示为：，

则令  ，

得

解得 ，从而或

代回或.

(2)因为表示的是终边落在四个象限的平分线上的角的集合；而集合表示终边落在坐标轴或四个象限平分线上的角的集合，从而：.

【总结升华】(1)从终边相同的角的表示入手分析问题，先表示出所有与角有相同终边的角，然后列出一个关于的不等式，找出相应的整数，代回求出所求解；(2)可对整数的奇、偶数情况展开讨论.

举一反三：

【变式1】集合，，则(    )

A、       B、       C、       D、

【答案】C

【解析】( 法一) 取特殊值-1，-3，-2，-1，0，1，2，3，4

(法二)在平面直角坐标系中，数形结合

(法三)集合M变形，

集合N变形，

是的奇数倍，是的整数倍，因此.

类型二:扇形的弧长和面积公式

例3．（2016 济南期中）已知扇形OAB的圆心角为120°，半径长为6 cm，求：

（1）弧的长；

（2）该扇形所含弓形的面积．

【思路点拨】（1）利用弧长公式，可得结论；

（2）首先求出扇形的面积，然后求出三角形OAB的面积，即可得出弓形的面积．

【答案】（1）4π；（2）

【解析】（1）∵，

∴

（2）∵∠OBD=30°r=6

∴OC=3

∴则

故

【总结升华】弧长和扇形面积的核心公式是圆周长公式和圆面积公式，当用圆心角的弧度数代替时，即得到一般的弧长公式和扇形面积公式：．

类型三：同角三角函数基本关系式

   例4．若sinθcosθ= ，θ∈(，)，求cosθ－sinθ的值．      

    【思路点拨】已知式为sinθ、cosθ的二次式，欲求式为sinθ、cosθ的一次式，为了运用条件，须将cosθ－sinθ进行平方．      

    【解析】 (cosθ－sinθ)2=cos2θ+sin2θ－2sinθcosθ=1－ = ．      

∵θ∈( ，)，∴ cosθ＜sinθ．    

∴cosθ－sinθ= － ． 

【总结升华】 sinθcosθ，cosθ+sinθ，cosθ－sinθ三者关系紧密，由其中之一，可求其余之二．    

    举一反三：   

 【变式1】已知是的一个内角，且，求

【思路点拨】根据可得的范围：再结合同角三角函数的关系式求解.

【答案】 

【解析】为钝角，

由，平方整理得

【变式2】已知cosθ－sinθ= －， 求sinθcosθ，sinθ+cosθ的值．      

 【答案】  

【解析】

，，

 ，

类型四：三角函数的诱导公式

例5．（2015春 湖南衡阳期末）已知，

（1）求的值

（2）求的值．

【答案】（1）；（2）32

【解析】由已知，所以，

（1）；

（2）

        ．

【总结升华】本题考查了三角函数的诱导公式以及基本关系式的混合运用；注意三角函数的名称以及符号．

举一反三：

【变式1】已知cos，且－π<α<－，则cos等于 (　　)

A.     B.        C．－     D．－

【答案】D

【解析】 cos＝cos

＝sin.

又－π<α<－，∴－π<＋α<－，

∴sin＝－，

∴cos＝－.

类型五：三角函数的图象和性质

例6. 函数y＝-xcosx的部分图象是(    )

【思路点拨】结合函数的奇偶性以及函数值的正负，或采用特殊值法.

【解析】因为函数y＝-xcosx是奇函数，它的图象关于原点对称，所以排除A、C，当x∈(0，)时，y＝-xcosx＜0.答案为D.

【总结升华】

本题通过观察四个选项A，C与B，D分别关于y轴和原点对称，从而启示我们从研究函数奇偶性入手考虑进行筛选，然后通过研究其函数值的符号进行确定，充分体现了数形结合的思想在解题中的应用.

举一反三：

【高清课堂：三角函数的综合395043 例1】

【变式1】函数在内 （  ）

A．没有零点                  B．有且仅有一个零点

C．有且仅有两个零点          D．有无穷多个零点

【答案】B

例7．已知函数的最小正周期为，为了得到函数     的图象，只要将的图象（     ） 

     A． 向左平移个单位长度      B．向右平移个单位长度

     C．向左平移个单位长度       D．向右平移个单位长度

【思路点拨】对于不同三角函数图象之间的平移变换，一定要根据诱导公式将二者之间变换清楚．

【答案】A

【解析】

由题知又，所以所以

     =

     =

显然将的图象向左平移个单位长度便可得到的图象．故选A．

举一反三：

【变式1】（2015 山东一模）函数（A＞0，ω＞0，）的图象如图所示，为了得到y=cos2x的图象，则只要将f（x）的图象（    ）

A．向左平移个单位长度    B．向右平移个单位长度

C．向左平移个单位长度    D．向右平移个单位长度

【答案】C

【解析】由图象可知A=1，T=π，∴

∴，又因为

∴，

∵，∴

∴

∴将函数f（x）向左平移可得到

故选C．

例8．函数()的最大值为3, 其图像相邻两条对称轴之间的距离为．

 (1)求函数的解析式;

(2)设,则,求的值.

【思路点拨】由题意知，A=2，，可求出．（2）把代入函数解析式，求出的值．

【答案】（1）（2）

【解析】(1)∵函数的最大值为3,∴即

∵函数图像的相邻两条对称轴之间的距离为,∴最小正周期为

∴,故函数的解析式为 ．

(2)∵

即

∵,∴

∴,故

【总结升华】由三角函数值，求角的时候，一定要注意角的范围．

举一反三：

【变式1】已知函数（其中）的周期为，且图象上一个最低点为.

  (Ⅰ)求的解析式；（Ⅱ）当，求的最值.

  【答案】(Ⅰ) （Ⅱ）最小值为1，最大值为．

【解析】（1）由最低点为

由

由点在图像上得即

又，   

（Ⅱ）

．