2022届中考数学专题复习训练——二次函数 专题3.2二次函数应用之建系问题学案

2021中考专项训练：二次函数应用

二、喷泉、拱形桥等建系问题

【经典例题1】北中环桥是省城太原的一座跨汾河大桥（如图1），它由五个高度不同，跨径也不同的抛物线型钢拱通过吊桥，拉索与主梁相连，最高的钢拱如图2所示，此钢拱（近似看成二次函数的图象-抛物线）在同一竖直平面内，与拱脚所在的水平面相交于A，B两点．拱高为78米（即最高点O到AB的距离为78米），跨径为90米（即AB=90米），以最高点O为坐标原点，以平行于AB的直线为x轴建立平面直角坐标系，则此抛物线钢拱的函数表达式为(     )

A．     B．C．    D．

【解析】设抛物线的解析式为：y=ax2，

将B(45，−78)代入得：−78=a×452，

解得：a=−，

故此抛物线钢拱的函数表达式为：y=−x2.

故选：B.

练习1-1某游乐园有一个直径为16米的圆形喷水池，喷水池的周边有一圈喷水头，喷出的水柱为抛物线，在距水池中心3米处达到最高，高度为5米，且各方向喷出的水柱恰好在喷水池中心的装饰物处汇合．如图所示，以水平方向为x轴，喷水池中心为原点建立直角坐标系．

（1）求水柱所在抛物线（第一象限部分）的函数表达式；

（2）王师傅在喷水池内维修设备期间，喷水管意外喷水，为了不被淋湿，身高1.8米的王师傅站立时必须在离水池中心多少米以内？

（3）经检修评估，游乐园决定对喷水设施做如下设计改进：在喷出水柱的形状不变的前提下，把水池的直径扩大到32米，各方向喷出的水柱仍在喷水池中心保留的原装饰物（高度不变）处汇合，请探究扩建改造后喷水池水柱的最大高度．

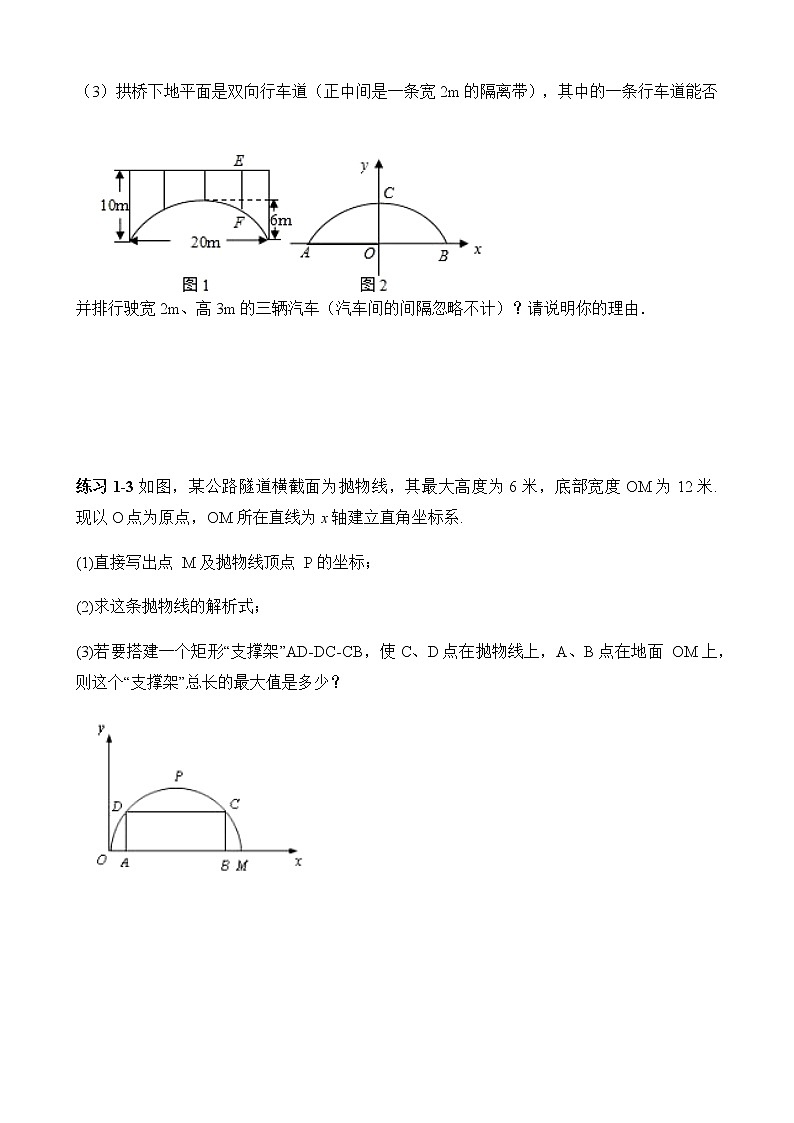
练习1-2一座拱桥的轮廓是抛物线型（如图 1 所示），拱高6m，跨度20m，相邻两支柱间的距离均为5m．

（1）将抛物线放在所给的直角坐标系中（如图2所示），求抛物线的解析式；

（2）求支柱 EF 的长度；

（3）拱桥下地平面是双向行车道（正中间是一条宽2m的隔离带），其中的一条行车道能否并排行驶宽2m、高3m的三辆汽车（汽车间的间隔忽略不计）？请说明你的理由．

练习1-3如图，某公路隧道横截面为抛物线，其最大高度为6米，底部宽度OM为12米. 现以O点为原点，OM所在直线为x轴建立直角坐标系.

(1)直接写出点 M及抛物线顶点 P的坐标；

(2)求这条抛物线的解析式；

(3)若要搭建一个矩形“支撑架”AD-DC-CB，使C、D点在抛物线上，A、B点在地面 OM上，则这个“支撑架”总长的最大值是多少？

练习1-4如图，小河上有一拱桥，拱桥及河道的截面轮廓线由抛物线的一部分ACB和矩形的三边AE，ED，DB组成，已知河底ED是水平的，ED＝16米，AE＝8米，抛物线的顶点C到ED距离是11米，以ED所在的直线为x轴，抛物线的对称轴y轴建立平面直角坐标系，

（1）求抛物线的解析式；

（2）已知从某时刻开始的40小时内，水面与河底ED的距离h（单位：米）随时间t（单位：时）的变化满足函数关系。

h=－（0≤t≤40）且当水面到顶点C的距离不大于5米时，需禁止船只通行，请通过计算说明：在这一时段内，需多少小时禁止船只通行？

练习1-5（2019•宁波模拟）某民房发生火灾．两幢大楼的部分截面及相关数据如图，小明在甲楼A处透过窗户E发现乙楼F处出现火灾，此时A，E，F在同一直线上．跑到一楼时，消防员正在进行喷水灭火，水流路线呈抛物线，在1.2m高的D处喷出，水流正好经过E，F．若点B和点E、点C和点F的离地高度分别相同，现消防员将水流抛物线向上平移5m，再向左后退　  　m，恰好把水喷到F处进行灭火．

练习1-6卢浦大桥拱形可以近似看作抛物线的一部分．在大桥截面1∶11000的比例图上，跨度AB＝5 cm，拱高OC＝0.9 cm，线段DE表示大桥拱内桥长，DE∥AB，如图（1）．在比例图上，以直线AB为x轴，抛物线的对称轴为y轴，以1 cm作为数轴的单位长度，建立平面直角坐标系，如图（2）．

　（1）求出图（2）上以这一部分抛物线为图象的函数解析式，写出函数定义域；

　 （2）如果DE与AB的距离OM＝0.45 cm，求卢浦大桥拱内实际桥长（备用数据：，计算结果精确到1米）．

【经典例题2】如图，排球运动员站在点O处练习发球，将球从O点正上方2 m的A处发出，把球看成点，其运行的高度y(m)与运行的水平距离x(m)满足关系式y＝a(x－6)2＋h.已知球网与O点的水平距离为9 m，高度为2.43 m，球场的边界距O点的水平距离为18 m.

(1)当h＝2.6时，求y与x的关系式；

(2)当h＝2.6时，球能否越过球网？球会不会出界？请说明理由；

(3)若球一定能越过球网，又不出边界，求h的取值范围．

【解析】(1)∵h=2.6，球从O点正上方2m的A处发出，

∴抛物线y=a(x−6)2+h过点(0，2)，

∴2=a(0−6)2+2.6，

解得：a=−，

故y与x的关系式为：y=−(x−6)2+2.6，

(2)当x=9时，y=−(x−6)2+2.6=2.45>2.43，

所以球能过球网；

当y=0时，−(x−6)2+2.6=0，

解得：x1=6+>18，x2=6-(舍去)

故会出界；

(3)当球正好过点(18，0)时，抛物线y=a(x−6)2+h还过点(0，2)，代入解析式得：

，解得，

此时二次函数解析式为：y=−(x−6)2+，

此时球若不出边界h⩾，

当球刚能过网，此时函数解析式过(9，2.43)，抛物线y=a(x−6)2+h还过点(0，2)，代入解析式得：，解得，

此时球要过网h⩾，

故若球一定能越过球网，又不出边界，h的取值范围是：h⩾.

练习2-1 2016年里约奥运会，中国跳水队赢得8个项目中的7块金牌，优秀成绩的取得离不开艰辛的训练。某跳水运动员在进行跳水训练时，身体(看成一点)在空中的运动路线是如图所示的一条抛物线，已知跳板AB长为2米，跳板距水面CD的高BC为3米，训练时跳水曲线在离起跳点水平距离1米时达到距水面最大高度k米，现以CD为横轴，CB为纵轴建立直角坐标系。

(1)当k=4时，求这条抛物线的解析式；

(2)当k=4时，求运动员落水点与点C的距离；

(3)图中CE=米，CF=米，若跳水运动员在区域EF内(含点E，F)入水时才能达到训练要求，求k的取值范围。

练习2-2一位篮球运动员投篮，球沿抛物线y=运行，然后准确落入篮筐内，已知篮筐的中心距离底面的距离为3.05m.

（1）求球在空中运行的最大高度为多少m？

（2）如果该运动员跳投时，球出手离地面的高度为2.25m，要想投入篮筐，则问他距离蓝筐中心的水平距离是多少？

练习2-3甲、乙两人进行羽毛球比赛，羽毛球飞行的路线为抛物线的一部分，如图，甲在O点正上方1m的P处发出一球，羽毛球飞行的高度y(m)与水平距离x(m)之间满足函数表达式，已知点O与球网的水平距离为5m，球网的高度为1.55m．

（1）当时，①求h的值；②通过计算判断此球能否过网．

（2）若甲发球过网后，羽毛球飞行到与点的O水平距离为7m，离地面的高度为m的Q处时，乙扣球成功，求a的值．

练习2-4小明跳起投篮，球出手时离地面，球出手后在空中沿抛物线路径运动，并在距出手点水平距离4m处达到最高4m．已知篮筐中心距地面3m，与球出手时的水平距离为8m，建立如图所示的平面直角坐标系．

（1）求此抛物线对应的函数关系式；

（2）此次投篮，球能否直接命中篮筐中心？若能，请说明理由；若不能，在出手的角度和力度都不变的情况下，球出手时距离地面多少米可使球直接命中篮筐中心？

（3）在篮球比赛中，当进攻方球员要投篮时，防守方球员常借身高优势及较强的弹跳封杀对方，这就是平常说的盖帽．（注：盖帽应在球达到最高点前进行，否则就是“干扰球”，属犯规．若此时，防守方球员乙前来盖帽，已知乙的最大摸球高度为3.19m，则乙在进攻方球员前多远才能盖帽成功？

参考答案

练习1-1

【解析】(1)设水柱所在抛物线(第一象限部分)的函数表达式为y=a(x−3)2+5(a≠0)，

将(8，0)代入y=a(x−3)2+5，得：25a+5=0，

解得：a=−，

∴水柱所在抛物线(第一象限部分)的函数表达式为y=−(x−3)2+5(0<x<8).

(2)当y=1.8时，有−(x−3)2+5=1.8，

解得：x1=−1，x2=7，

∴为了不被淋湿，身高1.8米的王师傅站立时必须在离水池中心7米以内。

(3)当x=0时，y=−(x−3)2+5=

设改造后水柱所在抛物线(第一象限部分)的函数表达式为y=−x2+bx+，

∵该函数图象过点(16，0)，

∴0=−×162+16b+，解得：b=3，

∴改造后水柱所在抛物线(第一象限部分)的函数表达式为y=−x2+3x+=−(x−)2+.

∴扩建改造后喷水池水柱的最大高度为。

练习1-2【解析】(1)根据题目条件A，B，C的坐标分别是(−10，0)，(10，0)，(0，6)，

设抛物线的解析式为y=ax2+c，

将B，C的坐标代入y=ax2+c，

得

解得.

所以抛物线的表达式y=−x2+6.

(2)可设F(5，yF)，于是

yF=−×52+6=4.5

从而支柱EF的长度是10−4.5=5.5米。

(3)设DN是隔离带的宽，NG是三辆车的宽度和，

则G点坐标是(7，0).

过G点作GH垂直AB交抛物线于H，

则yH=−×72+6=3.06>3.

根据抛物线的特点，可知一条行车道能并排行驶这样的三辆汽车。

练习1-3

【解析】(1)M(12，0)，P(6，6).(2分)

(2)设抛物线解析式为：

y=a(x−6)2+6(3分)

∵抛物线y=a(x−6)2+6经过点(0，0)

∴0=a(0−6)2+6，即a=−(4分)

∴抛物线解析式为：y=−(x−6)2+6，即y=−x2+2x.(5分)

(3)设A(m，0)，则B(12−m，0)，C(12−m，−m2+2m)

D(m，−m2+2m).(6分)

∴“支撑架”总长

AD+DC+CB=(−m2+2m)+(12−2m)+(−m2+2m)=−13m2+2m+12=−13(m−3)2+15，(8分)

∵此二次函数的图象开口向下。

∴当m=3米时，AD+DC+CB有最大值为15米.(9分)

练习1-4【解析】(1)∵点C到ED的距离是11米，

∴OC=11，

设抛物线的解析式为y=ax2+11，由题意得B(8，8)，

∴64a+11=8，

解得a=−，

∴y=−x2+11；

(2)水面到顶点C的距离不大于5米时，即水面与河底ED的距离h至多为11−5=6(米)，

∴6=−(t−19)2+8，

∴(t−19)2=256，

∴t−19=±16，

解得t1=35，t2=3，

∴35−3=32(小时).

答：需32小时禁止船只通行。

练习1-5

【解析】由图可知：A(0，21.2)，B(0，9.2)，C(0，6.2)，D(0，1.2)，

∵点B和点E. 点C和点F的离地高度分别相同，

∴E(20，9.2)，

设AE的直线解析式为y=kx+b，

，

∴k=−；b=21.2，

∴y=−x+21.2，

∵A，E，F在同一直线上。

∴F(25，6.2)，

设过D，E，F三点的抛物线为y=ax2+bx+c，

∴c=1.2；9.2=400a+20b+c；6.2=625a+25b+c，

∴y=−x2+x+，

水流抛物线向上平移5m，设向左退了m米，

∴D(0，6.2)，

设平移后的抛物线为y=−(x+m)2+(x+m)+1.2+5，经过点F，

∴m=5或m=−25(舍)，

∴向后退了5米。

故答案为5.

练习1-6【解析】（1）由于顶点C在y轴上，所以设以这部分抛物线为图象的函数解析式为

　　．

因为点A（，0）（或B（，0））在抛物线上，

所以，

得．

　　因此所求函数解析式为．

　（2）因为点D、E的纵坐标为，

所以，

得．

　所以点D的坐标为（，），点E的坐标为（，）．

　所以．

　因此卢浦大桥拱内实际桥长为 （米）．

练习2-1

(1)如图所示：

【解析】根据题意，可得抛物线顶点坐标M(3，4)，A(2，3)

设抛物线解析为：y=a(x−3)2+4，

则3=a(2−3)2+4，

解得：a=−1，

故抛物线解析式为：y=−(x−3)2+4；

(2)由题意可得：当y=0，则0=−(x−3)2+4，

解得：x1=1，x2=5，

故抛物线与x轴交点为：(5，0)，

当k=4时，求运动员落水点与点C的距离为5米；

(3)根据题意，抛物线解析式为：y=a(x−3)2+k，

将点A(2，3)代入可得：a+k=3，即a=3−k

若跳水运动员在区域EF内(含点E，F)入水，

则当x=时，y=a+k⩾0，即(3−k)+k⩾0，

解得：k⩽，

当x=时，y=+k⩽0，即(3−k)+k⩽0，

解得：k⩾，

故⩽k⩽.

练习2-2【解析】（1）∵y＝的顶点坐标为（0，），

∴球在空中运行的最大高度为m；

（2）当y＝3.05时，﹣0.2x2+3.5＝3.05，

解得：x＝±1.5，

∵x＞0，

∴x＝1.5；

当y＝2.25时，﹣0.2x2+3.5＝2.25，

解得：x＝2.5或x＝﹣2.5，

由1.5+2.5＝4（m），

故他距离篮筐中心的水平距离是4米．

练习2-3【解析】（1）①当a＝﹣时，y＝﹣（x﹣4）2+h，

将点P（0，1）代入，得：﹣×16+h＝1，

解得：h＝；

②把x＝5代入y＝﹣（x﹣4）2+，得：y＝﹣×（5﹣4）2+＝1.625，

∵1.625＞1.55，

∴此球能过网；

（2）把（0，1）、（7，）代入y＝a（x﹣4）2+h，得：，

解得：，

∴a＝﹣．

练习2-4

【解析】

（1）设抛物线为y＝a（x﹣4）2+4，

将（0，）代入，得a（0﹣4）2+4＝，

解得a＝﹣，

∴所求的解析式为y＝﹣（x﹣4）2+4；

（2）令x＝8，得y＝﹣（8﹣4）2+4＝≠3，

∴抛物线不过点（8，3），

故不能正中篮筐中心；

∵抛物线过点（8，），

∴要使抛物线过点（8，3），可将其向上平移个单位长度，故小明需向上多跳m再投篮（即球出手时距离地面3米）方可使球正中篮筐中心．

（3）由（1）求得的函数解析式，

当y＝3.19时，3.19＝﹣19（x﹣4）2+4

解得：x1＝6.7（不符合实际，要想盖帽，必须在篮球下降前盖帽，否则无效），

x2＝1.3

∴球员乙距离甲球员距离小于1.3米时，即可盖帽成功．