

2021年北京通州区树人瑞贝学校(初中部)七年级上期末数学试卷
展开
这是一份2021年北京通州区树人瑞贝学校(初中部)七年级上期末数学试卷,共7页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
一、选择题(共10小题;共50分)
1. −6 的绝对值等于
A. 6B. 16C. −16D. −6
2. 马虎同学做了以下 4 道计算题:① 0−−1=1;② 12÷−12=−1;③ −12+13=−16;④ −12018=2018.
请你帮他检查一下,他一共做对了
A. 1 题B. 2 题C. 3 题D. 4 题
3. 已知 2xn+1y3 与 13x4y3 是同类项,则 n 的值是
A. 2B. 3C. 4D. 5
4. 如图所示的主视图和俯视图对应的几何体(阴影所示为右)是
A. B.
C. D.
5. 下列方程中,与方程 2x−1=−5 解相同的方程是
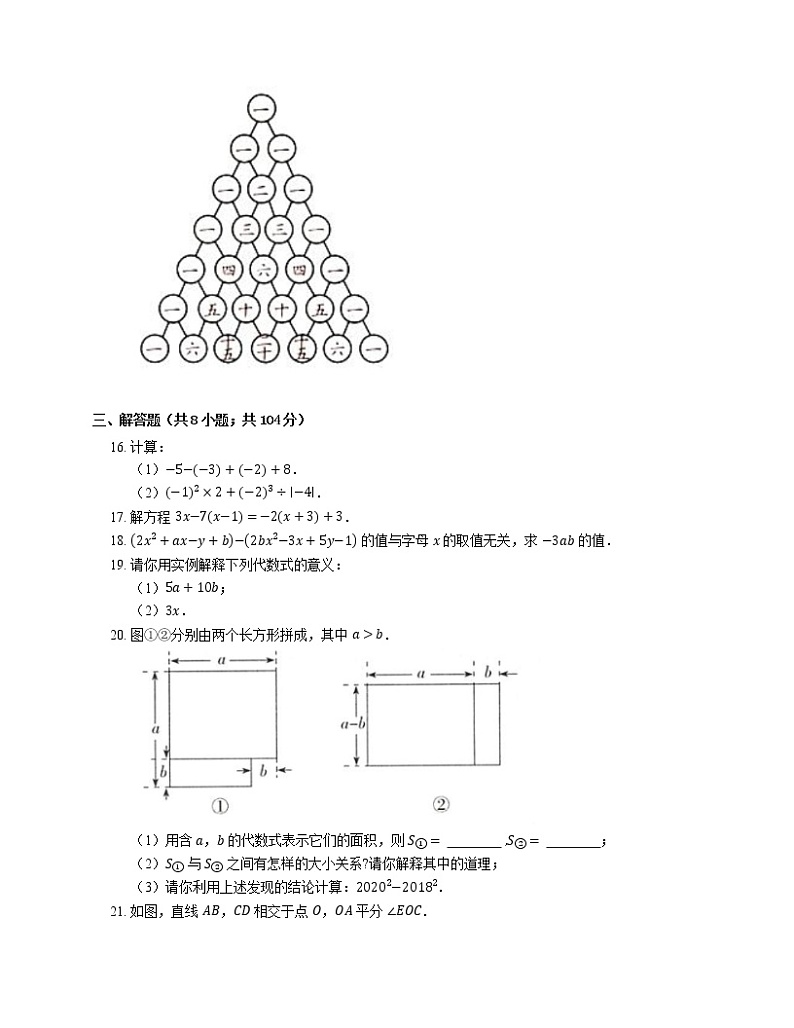
A. x−3=−2x−9B. x−3=2x
C. 2x+6=0D. 3x−6=0
6. 2020 年 7 月 23 日,中国首颗火量探测器“天问一号”成功发射,2021 年 2 月 10 日,在经过长达七个月,475000000 公里的漫长飞行之后,“天问一号”成功进入环火轨道.将 475000000 用科学记数法表示应为
A. 4.75×107B. 4.75×108C. 4.75×109D. 475×106
7. 在所有连接两点的线中
A. 直线最短B. 线段最短C. 弧线最短D. 射线最短
8. 某同学在计算 −3x2 乘一个多项式时错误的计算成了加法,得到的答案是 x2−x+1,由此可以推断正确的计算结果是
A. 4x2−x+1B. x2−x+1
C. −12x4+3x3−3x2D. 无法确定
9. 若 a=b,则在① a−13=b−13;② 13a=12b;③ −34a=−34b;④ 3a−1=3b−1 中,正确的有
A. 1 个B. 2 个C. 3 个D. 4 个
10. 甲、乙两人从同一个地点出发,沿着同一条线路进行赛跑练习,甲每秒跑 7 米,乙每秒跑 6.5 米,甲让乙先跑 5 米,设 x 秒后甲可以追上乙,则下面列出的方程不正确的是
A. 7x=6.5x+5B. 7x+5=6.5xC. 7x−6.5x=5D. 6.5x=7x−5
二、填空题(共5小题;共25分)
11. 比较大小:−57 −34.
12. 传统文化与创意营销的结合使已有近 600 年历史的故宫博物院重新焕发出生机,一些文创产品让顾客爱不释手.某购物网站上销售故宫文创笔记本和珐琅书签,若文创笔记本的销量比珐琅书签销量的 2 倍少 700 件,二者销量之和为 5900 件,用 x 表示珐琅书签的销量,则可列出一元一次方程 .
13. 有两根木条,一根长 60 厘米,另一根长 100 厘米,将它们的一端重合,放在同一条直线上,则两根木条的中点间的距离是 .
14. 设某数为 x,若它的 3 倍比这个数本身大 2,则可列出方程 .
15. 我国古代数学的许多创新与发展都曾居世界前列,其中“杨辉三角”(如图)就是一例,它的发现比欧洲早五百年左右.
杨辉三角两腰上的数都是 1,其余每个数为它的上方(左右)两数之和,事实上,这个三角形给出了 a+bnn=1,2,3,4,5,6 的展开式(按 a 的次数由大到小的顺序排列)的系数规律.例如,在三角形中第三行的三个数 1,2,1,恰好对应着 a+b2=a2+2ab+b2 展开式中各项的系数;第四行的四个数 1,3,3,1 , 恰好对应着 a+b3=a3+3a2b+3ab2+b3 展开式中各项的系数,等等.
(1)当 n=4 时,a+b4 的展开式中第 3 项的系数是 ;
(2)人们发现,当 n 是大于 6 的自然数时,这个规律依然成立,那么 a+b7 的展开式中各项的系数的和为 .
三、解答题(共8小题;共104分)
16. 计算:
(1)−5−−3+−2+8.
(2)−12×2+−23÷∣−4∣.
17. 解方程 3x−7x−1=−2x+3+3.
18. 2x2+ax−y+b−2bx2−3x+5y−1 的值与字母 x 的取值无关,求 −3ab 的值.
19. 请你用实例解释下列代数式的意义:
(1)5a+10b;
(2)3x.
20. 图①②分别由两个长方形拼成,其中 a>b.
(1)用含 a,b 的代数式表示它们的面积,则 S①= ,S②= ;
(2)S① 与 S② 之间有怎样的大小关系?请你解释其中的道理;
(3)请你利用上述发现的结论计算:20202−20182.
21. 如图,直线 AB,CD 相交于点 O,OA 平分 ∠EOC.
(1)若 ∠EOC=70∘,求 ∠BOD 的度数.
(2)若 ∠EOC:∠EOD=2:3,求 ∠BOD 的度数.
22. “十一”黄金周期间,百货大楼推出全场打 8 折的优惠活动,对于持贵宾卡的顾客可在打 8 折的基础上继续优惠.小明的妈妈持贵宾卡购买了标价为 10000 元的商品,一共节省了 2800 元
(1)用贵宾卡在打 8 折的基础上还能享受几折优惠?
(2)用贵宾卡在原价的基础上能享受几折优惠?
23. 如图,直线 AB,CD 相交于点 O,OF 平分 ∠COE,过点 O 作射线 OG,∠FOG=90∘.
(1)若 ∠AOE=80∘,∠COF=22∘,则 ∠BOD= ;
(2)若 ∠COE=40∘,试说明 OG 平分 ∠DOE.
答案
第一部分
1. A
2. C【解析】0−−1=0+1=1,①正确;
12÷−12=−1,②正确;
−12+13=−16,③正确;
−12018=1,④错误;
故选:C.
3. B【解析】∵2xn+1y3 与 13x4y3 是同类项,
∴n+1=4,解得,n=3.
4. B【解析】观察选项中的几何体,可知B选项中的几何体的主视图和俯视图与题图相符.
5. A
6. B
7. B
8. C【解析】∵x2−x+1−−3x2=4x2−x+1,
∴−3x2⋅4x2−x+1=−12x4+3x3−3x2.
故选:C.
9. C
10. B
【解析】设 x 秒后甲可以追上乙,
根据题意得:7x=6.5x+5,7x−6.5x=5,6.5x=7x−5.
故选:B.
第二部分
11. >
【解析】因为 57−34.
12. x+2x−700=5900
13. 80 cm 或 20 cm
14. 3x−x=2
15. 6,128
【解析】(1)当 n=4 时,a+b4 的展开式中第 3 项的系数是 6;
(2)人们发现,当 n 是大于 6 的自然数时,这个规律依然成立,当 n=7 时,各项系数分别为 1,7,21,35,35,21,71,
那么 a+b7 的展开式中各项的系数的和为 128.
第三部分
16. (1) 4.
(2) 0.
17.
3x−7x+7=−2x−6+3.3x−7x+2x=−6+3−7.−2x=−10.x=5.
18. 2x2+ax−y+b−2bx2−3x+5y−1=2x2+ax−y+b−2bx2+3x−5y+1=2−2bx2+a+3x−6y+b−1.
因为此式的值与 x 值无关,所以 2−2b=0,a+3=0,
所以 b=1,a=−3,
所以 −3ab=−3×−3×1=9.
19. (1) 答案不唯一,言之有理即可.
5a+10b 表示每支笔 a 元,每本笔记本 b 元,购买 5 支笔与 10 本笔记本的费用.
(2) 答案不唯一,言之有理即可.
3x 表示一辆车的行驶速度为 x km/h,3 小时行驶的路程.
20. (1) a2−b2;a+ba−b.
(2) S①=S②,相同的两个长方形拼成的两个图形的面积相等.
(3) 20202−20182=2020+2018×2020−2018=4038×2=8076.
21. (1) ∵OA 平分 ∠EOC,
∴∠AOC=12∠EOC=12×70∘=35∘,
∴∠BOD=∠AOC=35∘.
(2) 设 ∠EOC=2x,∠EOD=3x,
根据题意得 2x+3x=180∘,解得 x=36∘,
∴∠EOC=2x=72∘,
∴∠AOC=12∠EOC=12×72∘=36∘,
∴∠BOD=∠AOC=36∘.
22. (1) 设用贵宾卡在打 8 折的基础上还能享受 x 折优惠.
根据题意,得
10000×810×x10=10000−2800,
解得
x=9.
答:用贵宾卡在打 8 折的基础上还能享受 9 折优惠.
(2) 设用贵宾卡在原价的基础上能享受 y 折优惠.
根据题意,得
10000×1−y10=2800,
解得
y=7.2.
答:用贵宾卡在原价的基础上能享受 7.2 折优惠.
23. (1) 36∘
(2) 因为 ∠COE=40∘,OF 平分 ∠COE,
所以 ∠COF=∠EOF=12∠COE=20∘.
又 ∠FOG=90∘,
所以 ∠EOG=∠FOG−∠EOF=90∘−20∘=70∘,
∠COG=∠COF+∠FOG=20∘+90∘=110∘,
所以 ∠DOG=180∘−∠COG=70∘.
所以 ∠EOG=∠DOG=70∘,
所以 OG 平分 ∠DOE.
相关试卷
这是一份2021年北京昌平区昌平下庄学校(初中部)九年级上期末数学试卷,共17页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
这是一份2021年北京朝阳区立华学校(初中部)九年级上期末数学试卷,共13页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
这是一份2021年北京顺义区高丽营学校(初中部)九年级上期末数学试卷,共11页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。









