2021年北京延庆区体育运动学校七年级上期末数学试卷

这是一份2021年北京延庆区体育运动学校七年级上期末数学试卷，共11页。试卷主要包含了选择题，填空题，解答题，羊二，直金十九两；牛二等内容，欢迎下载使用。
一、选择题（共10小题；共50分）
1. 12020 的倒数是
A. −12020B. 12020C. 2020D. −2020

2. 去年深圳市在高新技术成果交易会共吸引来自各国 546000 参观人次，其中 546000 用科学记数法表示为
A. 546×103B. 54.6×104C. 5.46×105D. 0.546×106

3. “打通一条隧道，就能缩短路程”其中蕴含的数学道理是
A. 两点之间，线段最短B. 两点确定一条直线
C. 过一点，有无数条直线D. 线动成面

4. 下列等式变形正确的是
A. −2x=5，则 x=−25
B. x5+x−12=1，则 2x+5x−1=1
C. 若 5x−6=2x+8，则 5x+2x=6+8
D. 若 7x+1−9x=1，则 7x+7−9x=1

5. 计算 −9x2+7x2−3x2+6x2−x2 的结果是
A. x2B. 1C. 0D. −x2

6. 若代数式 2a2+3a=1，那么代数式 4a2+6a−10 的值是
A. −8B. 16C. 1D. 6

7. 实数 a，b，c 在数轴上对应点的位置如图所示，则下列结论中正确的是
A. a+c>0B. b+c>0C. ac>bcD. a−c>b−c

8. 一个角的补角加上 10∘ 后，等于这个角的余角的 3 倍，则这个角是
A. 30∘B. 35∘C. 40∘D. 45∘

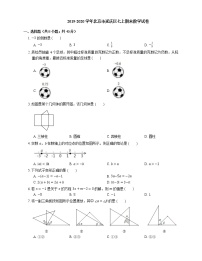
9. 下列四张正方形硬纸片，剪去阴影部分后，如果沿虚线折叠，可以围成一个封闭的长方体包装盒的是
A. B.
C. D.

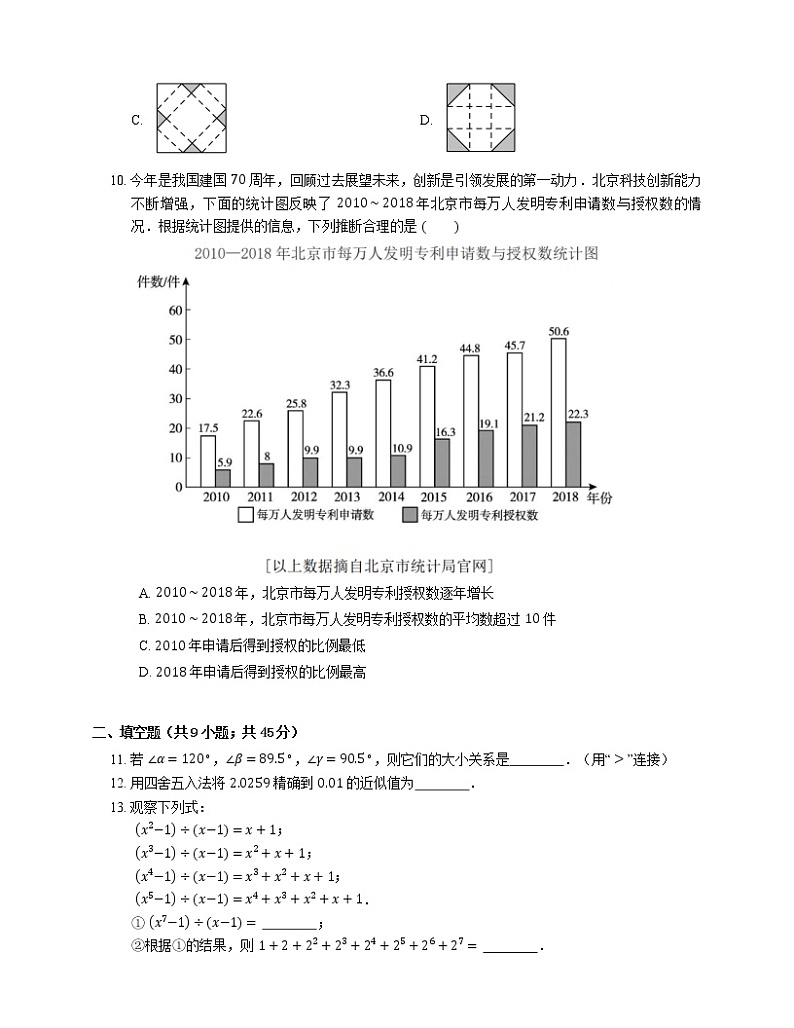
10. 今年是我国建国 70 周年，回顾过去展望未来，创新是引领发展的第一动力．北京科技创新能力不断增强，下面的统计图反映了 2010∼2018 年北京市每万人发明专利申请数与授权数的情况．根据统计图提供的信息，下列推断合理的是
A. 2010∼2018 年，北京市每万人发明专利授权数逐年增长
B. 2010∼2018 年，北京市每万人发明专利授权数的平均数超过 10 件
C. 2010 年申请后得到授权的比例最低
D. 2018 年申请后得到授权的比例最高

二、填空题（共9小题；共45分）
11. 若 ∠α=120∘，∠β=89.5∘，∠γ=90.5∘，则它们的大小关系是 ．（用“>”连接）

12. 用四舍五入法将 2.0259 精确到 0.01 的近似值为 ．

13. 观察下列式：
x2−1÷x−1=x+1；
x3−1÷x−1=x2+x+1；
x4−1÷x−1=x3+x2+x+1；
x5−1÷x−1=x4+x3+x2+x+1．
① x7−1÷x−1= ；
②根据①的结果，则 1+2+22+23+24+25+26+27= ．

14. 若关于 x 的方程 ax+3=2x−1 的解为正整数，则所有满足条件的整数 a 的值为 ．

15. 若 a−32+∣a+b−2∣=0，那么 ba= ．

16. 定义运算“\（\mathbin{\dividentimes}\）“：\（a\mathbin{\dividentimes}b=ab+a-b\），如果 \（x\mathbin{\dividentimes}\left（-4\right）=58\），则 x= ．

17. 有两根木条，一根长 60 厘米，另一根长 100 厘米，将它们的一端重合，放在同一条直线上，则两根木条的中点间的距离是 ．

18. 某校要组织体育活动，体育委员小明带 x 元去买体育用品．若全买羽毛球拍刚好可以买 20 副，若全买乒乓球拍刚好可以买 30 个，已知每个乒乓球拍比每副羽毛球拍便宜 5 元，依题意，可列方程为 ．

19. 现规定 abcd=a−b+c−d，则 xy−3x2−2xy−x2−2x2−3−5+xy 的值为 ．

三、解答题（共11小题；共143分）
20. 计算：
（1）13+−15−−23．
（2）−74×−15÷−75．

21. 计算：
（1）−6×−12+23．
（2）−12012−2÷12×3+22．

22. 解方程组 2x+4y=5,x=1−y.

23. 符号“f”表示一种运算，fx 表示 x 在运算 f 作用下的结果，如 fx=2x+1 表示 x 在运算 f 作用下的结果，它对一些数或式的运算结果如下：
f1=2×1+1=3，f−3=2×−3+1=−5，fm+1=2m+1+1=2m+3，⋯
利用以上规律计算：
（1）f2021−f2020．
（2）f2m2+3n−f2m2−3n．

24. 解方程：x−x−12=2−x+24．

25. 一个角的余角比它的补角的 13 还少 20∘，求这个角的度数．

26. 如图是—“数值转换机”．
（1）若第 1 次输入的数为 2，则第 1 次输出的数为 1，那么第 2 次输出的数为 ．
（2）若输入的数为 5，则第 2018 次输出的数是 ．

27. 我国传统数学名著《九章算术》记载：“今有牛五、羊二，直金十九两；牛二、羊五，直金十六两．问牛、羊各直金几何?”译文：“假设有 5 头牛、 2 只羊，值 19 两银子；2 头牛、 5 只羊，值 16 两银子，问每头牛、每只羊分别值银子多少两?”根据以上译文，提出以下两个问题：
（1）求每头牛、每只羊各值多少两银子?
（2）若某商人准备用 19 两银子买牛和羊（要求既有牛也有羊，且银两须全部用完），请问商人有几种购买方法?列出所有的可能．

28. 已知 A，B，C 三点在数轴上对应的位置如图如示．其中点 B 对应的数为 2，BC=3，AB=14．
（1）点 A 对应的数是 ，点 C 对应的数是 ．
（2）动点 P，Q 分别同时从 A，C 两点出发，分别以每秒 8 个单位和 3 个单位的速度沿数轴正方向运动．点 M 为 AP 的中点，点 N 在 CQ 上，且 CN=13CQ，设运动时间为 tt>0．
①请直接用含 t 的代数式表示点 M，N 对应的数．
②当 OM=2BN 时，求 t 的值．

29. 我们熟知的七巧板，是由宋代黄伯思设计的”燕几图”（”燕几”就是”宴几”，也就是宴请宾客的案几）演变而来．到了明代，严澄将”燕几图”里的方形案几改为三角形，发明了”蝶翅几”，而到了清代初期，在”燕几图”和”蝶翅几”的基础上，兼有三角形、正方形和平行四边形，能拼出更加生动、多样图案的七巧板就问世了（如图 1 网格中所示）．
（1）若正方形网格的边长为 1，则图 1 中七巧板的七块拼板的总面积为 ；
（2）使用图 1 中的七巧板可以拼出一个轮廓如图 2 所示的长方形，请在图 2 中画出拼图方法；（要求：画出各块拼板的轮廓）
（3）随着七巧板的发展，出现了一些形式不同的七巧板如图 3 所示的是另一种七巧板．利用图 3 中的七巧板可以拼出一个轮廓如图 4 所示的图形：大正方形的中间去掉一个小正方形．请在图 4 中画出拼图方法（要求：画出各块拼板的轮廓）

30. 如图 1，射线 OC 在 ∠AOB 的内部，图中共有 3 个角：∠AOB，∠AOC 和 ∠BOC，若其中有一个角的度数是另一个角的度数的两倍，则称射线 OC 是 ∠AOB 的“奇妙线”．
（1）一个角的平分线 这个角的“奇妙线”．（填“是”或“不是”）
（2）如图 2，若 ∠MPN=60∘，射线 PQ 绕点 P 从 PN 位置开始，以每秒 10∘ 的速度逆时针旋转，当 ∠QPN 首次等于 180∘ 时停止旋转，设旋转的时间为 ts．
①当 t 为何值时，射线 PM 是 ∠QPN 的“奇妙线”?
②若射线 PM 同时绕点 P 以每秒 6∘ 的速度逆时针旋转，并与 PQ 同时停止旋转．请求出当射线 PQ 是 ∠MPN 的“奇妙线”时 t 的值．
答案
第一部分
1. C【解析】12020 的倒数是 2020．
2. C
3. A【解析】“打通一条隧道，就能缩短路程”其中蕴含的数学道理是两点之间，线段最短．
4. D【解析】A．−2x=5，等式两边同时除以 −2 得：x=−52，即A项错误；
B．x5+x−12=1，等式两边同时乘以 10 得：2x+5x−1=10，即B项错误；
C．若 5x−6=2x+8，移项得：5x−2x=8+6，即C项错误；
D．7x+1−9x=1，去括号得：7x+7−9x=1，即D项正确．
5. C
6. A【解析】4a2+6a−10 变形得到 22a2+3a−10，将 2a2+3a=1 代入 22a2+3a−10 得到 2×1−10=−8．
7. D【解析】∵c