2021届湖南省长沙市高三第一次模拟试卷数学理科试题Word版含答案

这是一份2021届湖南省长沙市高三第一次模拟试卷数学理科试题Word版含答案，共21页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
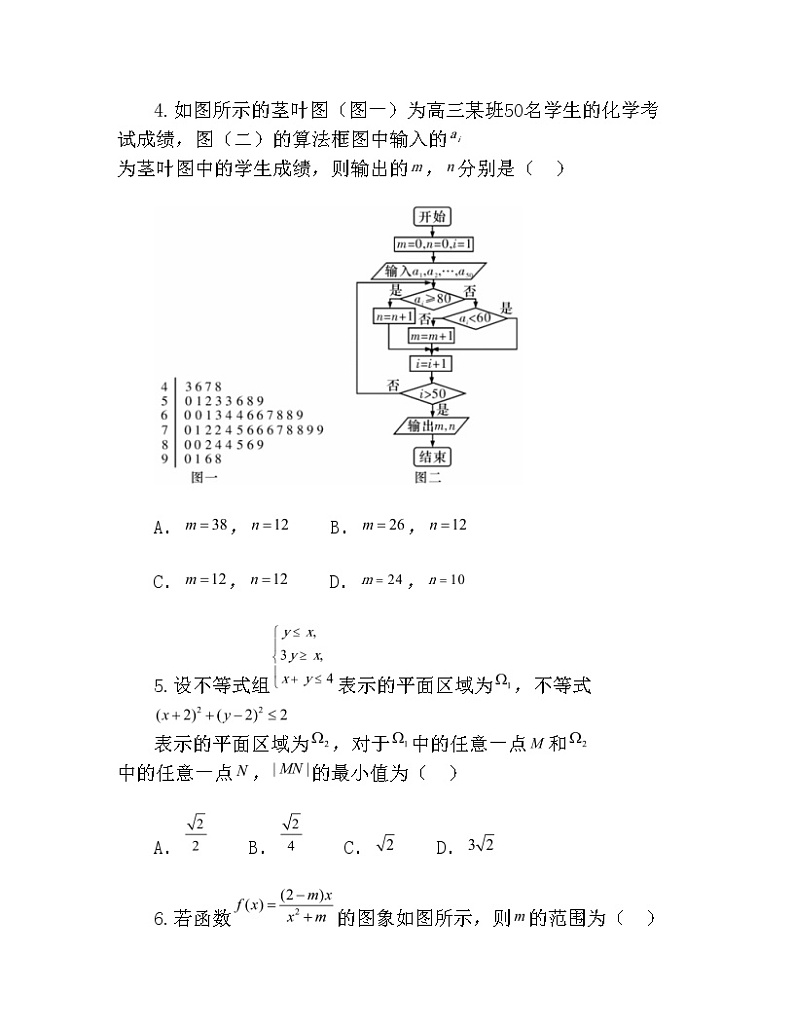
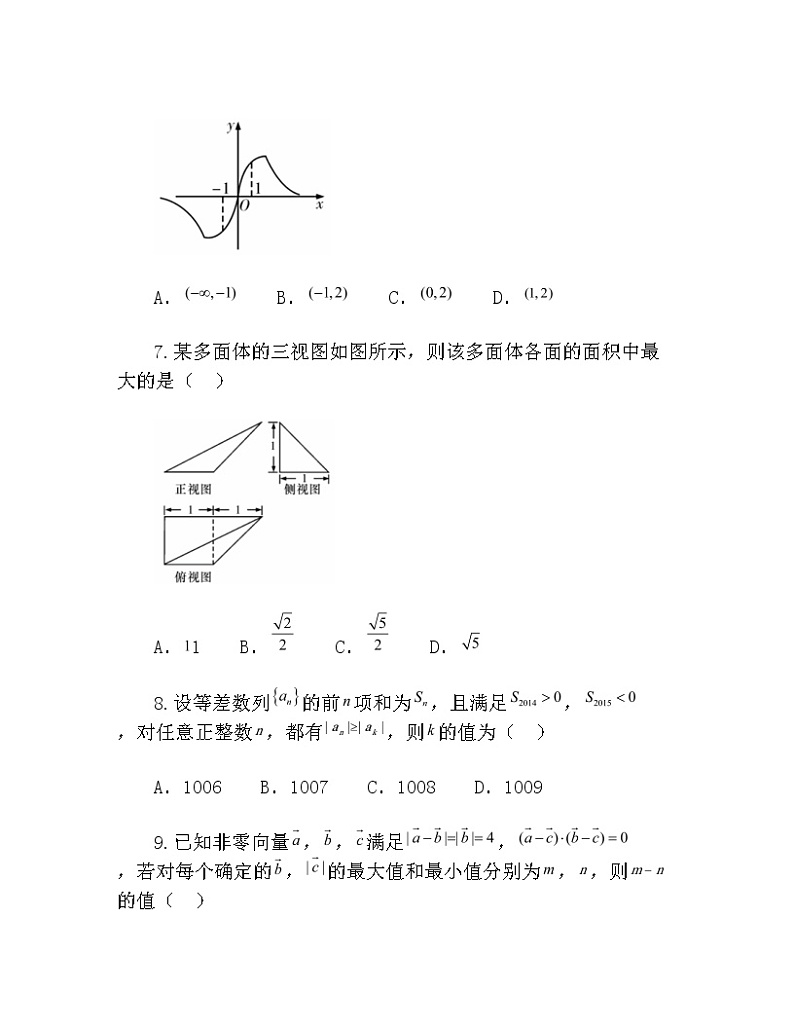
2021届湖南省长沙市高三第一次模拟试卷 数学理科试题 第Ⅰ卷（共60分） 一、选择题：本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中，只有一项是符合题目要求的. 1.设复数，在复平面内的对应点关于实轴对称，，则（  ） A．    B．    C．    D． 2.设全集，函数的定义域为，集合，则的子集个数为（  ） A．7    B．3    C．8    D．9  3.函数（，）的图象中相邻对称轴的距离为，若角的终边经过点，则的值为（  ） A．    B．    C．    D． 4.如图所示的茎叶图（图一）为高三某班50名学生的化学考试成绩，图（二）的算法框图中输入的为茎叶图中的学生成绩，则输出的，分别是（  ）  A．，    B．， C．，    D．， 5.设不等式组表示的平面区域为，不等式表示的平面区域为，对于中的任意一点和中的任意一点，的最小值为（  ） A．    B．    C．    D． 6.若函数的图象如图所示，则的范围为（  ）  A．    B．    C．    D． 7.某多面体的三视图如图所示，则该多面体各面的面积中最大的是（  ）  A．1    B．    C．    D． 8.设等差数列的前项和为，且满足，，对任意正整数，都有，则的值为（  ） A．1006    B．1007    C．1008    D．1009  9.已知非零向量，，满足，，若对每个确定的，的最大值和最小值分别为，，则的值（  ） A．随增大而增大    B．随增大而减小 C．是2    D．是4  10.已知如图所示的三棱锥的四个顶点均在球的球面上，和所在的平面互相垂直，，，，则球的表面积为（  ）  A．    B．    C．    D． 11.已知双曲线：（，）的右顶点为，为坐标原点，以为圆心的圆与双曲线的某渐近线交于两点，，若，且，则双曲线的离心率为（  ） A．    B．    C．    D． 12.已知为自然对数的底数，若对任意的，总存在唯一的，使得成立，则实数的取值范围是（  ） A．    B．    C．    D． 第Ⅱ卷（共90分） 二、填空题（每题5分，满分20分，将答案填在答题纸上） 13.已知，展开式的常数项为15，． 14.设，，关于，的不等式和无公共解，则的取值范围是． 15.正项数列的前项和为，且（），设，则数列的前2016项的和为． 16.已知是椭圆：的右焦点，是上一点，，当周长最小时，其面积为． 三、解答题 （本大题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.）  17.如图，在中，已知点在边上，且，，，．  （1）求的长； （2）求． 18.如图，在多面体中，四边形为梯形，，均为等边三角形，，．  （1）过作截面与线段交于点，使得平面，试确定点的位置，并予以证明； （2）在（1）的条件下，求直线与平面所成角的正弦值． 19.2015年7月9日21时15分，台风“莲花”在我国广东省陆丰市甲东镇沿海登陆，造成165.17万人受灾，5.6万人紧急转移安置，288间房屋倒塌，46.5千公顷农田受灾，直接经济损失12.99亿元．距离陆丰市222千米的梅州也受到了台风的影响，适逢暑假，小明调查了梅州某小区的50户居民由于台风造成的经济损失，将收集的数据分成，，，，五组，并作出如图频率分布直方图：  （1）试根据频率分布直方图估计小区平均每户居民的平均损失（同一组中的数据用该组区间的中点值代表）； （2）小明向班级同学发出倡议，为该小区居民捐款，现从损失超过4000元的居民中随机抽取2户进行捐款援助，设抽出损失超过8000元的居民为户，求的分布列和数学期望； （3）台风后区委会号召小区居民为台风重灾区捐款，小明调查的50户居民捐款情况如图，根据图表格中所给数据，分别求，，，，，，的值，并说明是否有以上的把握认为捐款数额多于或少于500元和自身经济损失是否到4000元有关？  经济损失不超过4000元经济损失超过4000元合计捐款超过500元 捐款不超过500元 合计    0.150.100.050.0250.0100.0050.0012.0722.7063.8415.0246.6357.87910.828 附：临界值表参考公式：，． 20.已知抛物线的顶点在原点，其焦点（）到直线：的距离为，设为直线上的点，过点作抛物线的两条切线，，其中，为切点． （1）求抛物线的方程； （2）当点为直线上的定点时，求直线的方程； （3）当点在直线上移动时，求的最小值． 21.已知函数，点在曲线上，且曲线在点处的切线与直线垂直． （1）求，的值； （2）如果当时，都有，求的取值范围．  请考生在22、23两题中任选一题作答，如果多做，则按所做的第一题记分. 22.选修4-4：坐标系与参数方程 已知曲线的参数方程是（为参数），以坐标原点为极点，轴的正半轴为极轴建立极坐标系，曲线的极坐标方程是，正方形的顶点都在上，且，，，依逆时针次序排列，点的极坐标为． （1）求点，，，的直角坐标； （2）设为上任意一点，求的取值范围． 23.选修4-5：不等式选讲 设，记的解集为． （1）求集合； （2）已知，比较与的大小． 2021届湖南省长沙市高三第一次模拟试卷 数学理科试题参考答案 一、选择题 1-5:      6-10:      11、12： 二、填空题 13.          14.          15.          16.4 三、解答题 17.解：（1）因为，则， 所以，即． 在中，由余弦定理，可知． 即，解得，或． 因为，所以． （2）在中，由正弦定理，可知， 又由，可知， 所以． 因为，所以． 18.解：（1）当为线段的中点时，使得平面． 证法如下： 连接，，设， ∵四边形为矩形， ∴为的中点， 又∵为的中点， ∴为的中位线， ∴， ∵平面，平面， ∴平面，故为的中点时，使得平面．  （2）过作分别与，交于，， 因为为的中点，所以，分别为，的中点， ∵与均为等边三角形，且， ∴，连接，，则得， ∵，，， ∴，， ∴四边形为等腰梯形． 取的中点，连接，则， 又∵，，， ∴平面， 过点作于，则， ∴，． 分别以，，的方向为，，轴的正方向，建立空间直角坐标系，不妨设，则由条件可得：，，，，，． 设是平面的法向量， 则即 所以可取， 由，可得， ∴直线与平面所成角的正弦值为．  19.解：（1）记每户居民的平均损失为元， 则 ． （2）由频率分布直方图，可得超过4000元的居民共有户，损失超过8000元的居民共有户， 因此的可能值为0,1,2， ，，， 的分布列为： 012 ． （3）解得，，，，，，， ， 所以有以上的把握认为捐款数额多于或少于500元和自身经济损失是否到4000元有关．　 20.解：（1）依题意，设抛物线的方程为，由，结合，解得． 所以抛物线的方程为． （2）抛物线的方程为，即，求导得， 设，（其中，）， 则切线，的斜率分别为，， 所以切线的方程为，即， 即． 同理可得切线的方程为， 因为切线，均过点，所以，， 所以，为方程的两组解， 所以直线的方程为． （3）由抛物线定义可知，， 所以， 联立方程消去整理得． 由一元二次方程根与系数的关系可得，， 所以， 又点在直线上，所以， 所以， 所以当时，取得最小值，且最小值为． 21.解：（1）， 依题意，，解得． （2）由（1）可知，代入得 ，即， 因为当时，，时，，所以， 所以，即， 令，设，则， 又． ①当，即时，恒成立， 所以在上单调递增，所以 （i）当时，，又因为此时，， 所以，即成立； （ii）当时，，又因为此时，， 所以，即成立． 因此当时，当时，都有成立，符合题意． ②当，即时，由，得，， 因为，所以，， 当时，，所以在上递减，所以， 又因为此时，，所以，即 与矛盾，所以不符合题意． 综上可知：的取值范围是． 22.解：（1）点，，，的极坐标为，，，， 点，，，的直角坐标为，，，. （2）设，则（为参数）， ． 23.解：（1） 由，得或或 解得， 故． （2）由（1）知， 因为， 当时，，所以； 当时，，所以； 当时，，所以． 综上所述：当时，； 当时，； 当时，．