初中22.1.1 二次函数教学ppt课件

这是一份初中22.1.1 二次函数教学ppt课件，共17页。PPT课件主要包含了学习目标，知识精讲，yax2，y-ax2，位置开口方向，对称性，顶点最值，增减性，开口向上在x轴上方，开口向下在x轴下方等内容，欢迎下载使用。

会用描点法画出二次函数y=ax²的图象，概括出图象的特点.
掌握形如y=ax²的二次函数图象的性质，并会进行简单应用.
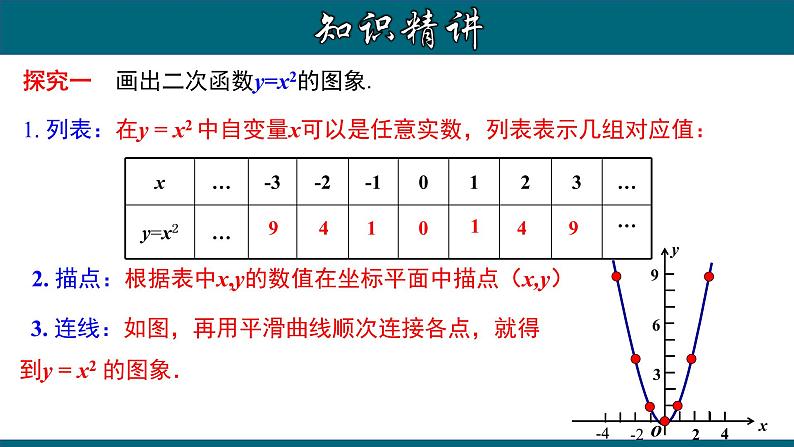
探究一 画出二次函数y=x2的图象.
1. 列表：在y = x2 中自变量x可以是任意实数，列表表示几组对应值：
2. 描点：根据表中x,y的数值在坐标平面中描点（x,y）
3. 连线：如图，再用平滑曲线顺次连接各点，就得到y = x2 的图象．
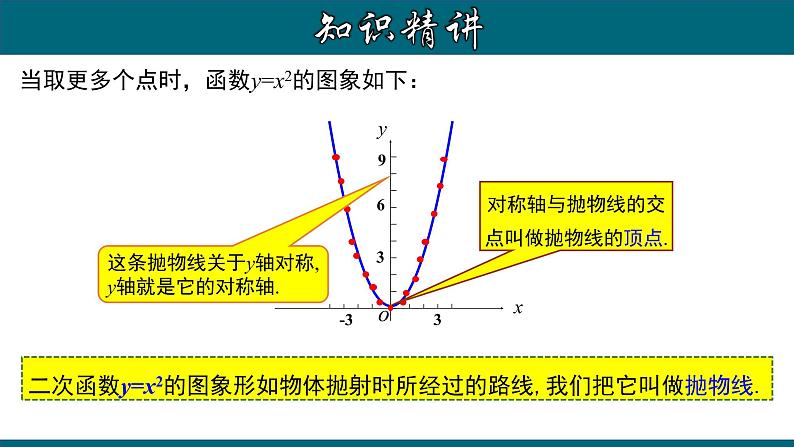
当取更多个点时，函数y=x2的图象如下：
二次函数y=x2的图象形如物体抛射时所经过的路线,我们把它叫做抛物线.
这条抛物线关于y轴对称, y轴就是它的对称轴.
对称轴与抛物线的交点叫做抛物线的顶点.
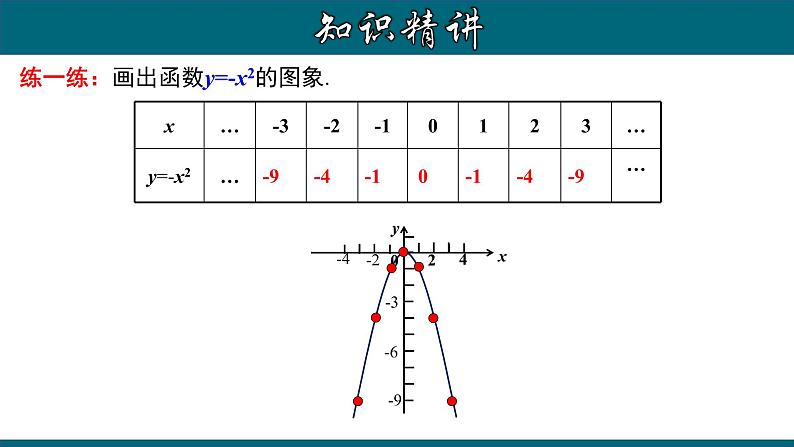
练一练：画出函数y=-x2的图象.
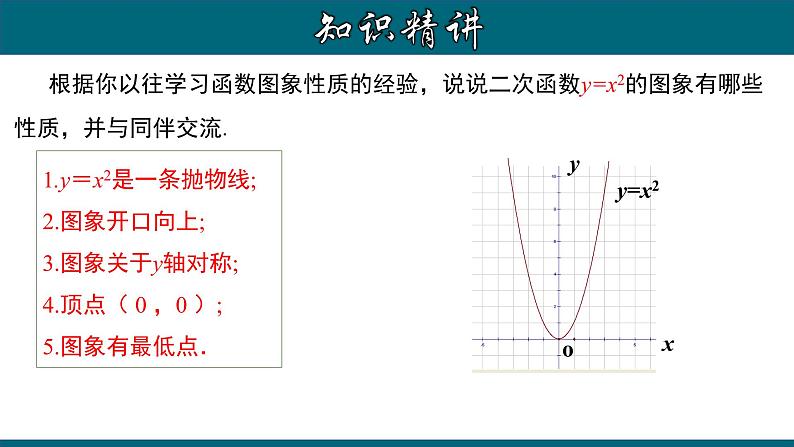
根据你以往学习函数图象性质的经验，说说二次函数y=x2的图象有哪些性质，并与同伴交流.
1.y＝x2是一条抛物线;2.图象开口向上;3.图象关于y轴对称;4.顶点（ 0 ，0 ）;5.图象有最低点．
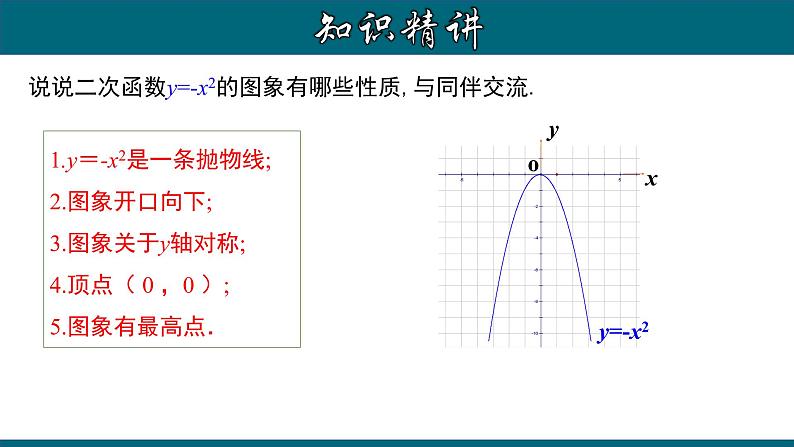
说说二次函数y=-x2的图象有哪些性质,与同伴交流.
1.y＝-x2是一条抛物线;2.图象开口向下;3.图象关于y轴对称;4.顶点（ 0 ，0 ）;5.图象有最高点．
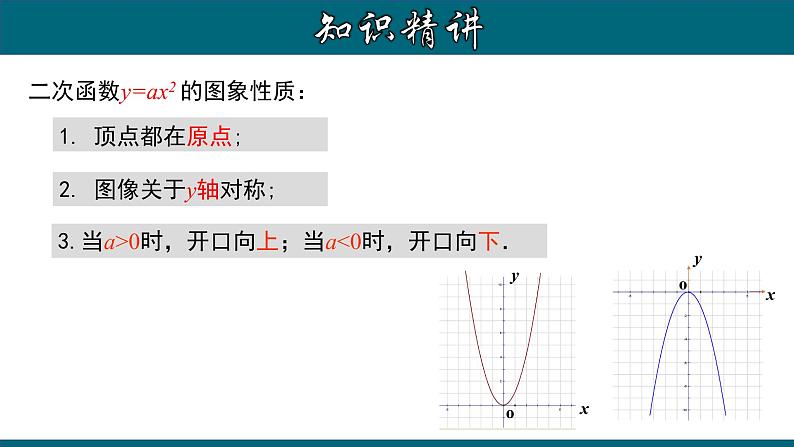
1. 顶点都在原点;
3.当a>0时，开口向上；当a<0时，开口向下．
二次函数y=ax2 的图象性质：
2. 图像关于y轴对称;
观察下列图象，抛物线y=ax2与y=-ax2（a＞0)的关系是什么？
二次项系数互为相反数，开口相反，大小相同，它们关于x轴对称.
探究二 观察图形，y随x的变化如何变化？
对于抛物线 y = ax 2 （a＞0）当x＞0时，y随x取值的增大而增大；当x<0时，y随x取值的增大而减小.
观察图形，y随x的变化如何变化？
对于抛物线 y = ax 2 （a＜0） 当x＞0时，y随x取值的增大而减小；当x<0时，y随x取值的增大而增大.
关于y轴对称，对称轴是直线x＝0
顶点坐标是原点（0，0）
当x=0时，y最小值=0
当x=0时，y最大值=0
在对称轴左侧递减在对称轴右侧递增
在对称轴左侧递增在对称轴右侧递减
3.函数y= x2的图象的开口 ,对称轴是 , 顶点是 ;顶点是抛物线的最 点
2.函数y=－3x2的图象的开口 ,对称轴是 ,顶点是 顶点是抛物线的最 点
1.函数y=4x2的图象的开口 ,对称轴是 ,顶点是 ;
4.函数y= －0.2x2的图象的开口 ,对称轴是___,顶点是 ;
m+1>0 ①
解②得:m1=－2, m2=1
此时,二次函数为: y=2x2.